马克思的社会扩大再生产优化的图解法
2015-12-11陶为群
陶为群
研究解决社会扩大再生产的优化问题,对于深化马克思的社会再生产理论以及对现实经济宏观调控的指导,都具有重要的理论意义。马克思的社会扩大再生产的优化,是指在对于马克思的社会扩大再生产公式获得解析解的基础上,进一步获得最优解析解。马克思的社会扩大再生产的优化问题,是对于扩大再生产公式的求解问题增加了目标函数,因而当获得社会扩大再生产公式的解,还只是获得了扩大再生产的可行解而不是最优解。已经有研究运用多参数线性规划方法解决了马克思的两大部类扩大再生产的优化问题(陶为群、陶川,2012),[1]但运算比较复杂。也有研究运用“价值系数法”替代单纯形法,简化了两大部类扩大再生产优化问题的求解方法(陶为群、陶川,2013),[2]但是仍然不够直观、简便。最近,又有研究提出了马克思扩大再生产公式的图解法,可以直观、方便地获得扩大再生产公式的解析解(陶为群,2015)。[3]基于这个图解法的启示,本文提出马克思的社会扩大再生产优化的图解法,即应用平面解析几何方法,通过作图获得社会扩大再生产的最优解析解。用马克思的社会扩大再生产优化的图解法,可以替代已有的两大部类扩大再生产的优化问题的各种求解方法,直观、方便地获得社会扩大再生产的最优解,切实简化社会扩大再生产优化问题的求解。
一、马克思的社会扩大再生产优化的约束条件和目标函数
按照马克思社会再生产理论,社会生产部门划分成生产资料、消费资料的两个部类,分别记为第Ⅰ、Ⅱ部类。第j部类(j=Ⅰ,Ⅱ。下同)在t年初时点的总资本分解成用于购买生产资料的不变资本、购买劳动力的可变资本两个部分,分别记为Cj(t)和Vj(t),Cj(t)和 Vj(t)都是每年周转一次;Vj(t)带来剩余价值 Mj(t)。第j部类产品当中消耗的不变资本对于可变资本的固定不变倍数hj表示该部类的资本有机构成。剩余价值Mj(t)与可变资本Vj(t)之间保持固定不变的比率,以ej表示,是第j部类的剩余价值率。以Yj(t)表示第j部类的新创造价值,对确定了含义的字母前面加符号△表示在当年再生产过程中所形成的增量,以Mx(t)j表示第j部类企业所有者把本部类的剩余价值中用于个人消费的部分。由于剩余价值Mj(t)是形成本部类的新增资本和企业所有者的剩余价值消费的唯一来源,所以有剩余价值使用的行为方程:

有研究结果根据式(1)和政治经济学教科书中说明的社会再生产的实现条件(程恩富等,2012),[4]获得社会再生产的资本积累均衡方程式(2),并且基于资本积累均衡方程用图解法求解马克思扩大再生产公式。[3]

如果对于扩大再生产确定目标函数,就可以在马克思扩大再生产公式的图解法的基础上,形成马克思的社会扩大再生产优化的图解法。这里以第j部类新增的新创造价值(产品)△Yj(t)一般地代表该部类新增的社会产品,由于每个部类内部各部分的相互关系固定不变,一个部类新创造价值最大化与利润最大化具有等价性。那么,下一年相对于本年两个部类新增的新创造价值(产品)总和△Y(t)是:

可以把△Y(t)取得最大值确定为扩大再生产的目标函数。因为第j部类的新创造价值(产出)与不变资本之间的比率即不变资本产出率Yj(t)│Cj(t)固定不变,是(1+ej)│hj,因而:

把式(4)代入式(3),得到:

只要两个部类的不变资本产出率不相等也就是(1+eI)│hI≠(1+eII)hII,就可以通过将待定变量△CI(t)和 △CII(t)选择特定的匹配,使式(5)所表示的新增的新创造价值总和△Y(t)取得最大值。
二、在第Ⅰ部类的不变资本产出率高条件下扩大再生产优化的图解法
扩大再生产的目标函数式(5)中有两个待定变量△CI(t)和△CII(t)。扩大再生产公式的图解法是基于资本积累均衡方程(2)以及对于两个待定变量的条件,应用平面解析几何方法,通过作图获得扩大再生产公式的解析解。而社会扩大再生产优化的图解法,就是以扩大再生产公式的解析解为基础,进一步获得使目标函数式(5)取得最大值的最优解析解。
如图1所示,分别以变量△CI(t)和△CII(t)作为横、纵坐标建立直角坐标系。由于受到剩余价值使用的行为方程式(1)的约束,△CI(t)和 △CII(t)的取值范围局限在由两条直线△CI(t)=MIhI│(1+hI)和△CII(t)=MIIhII│(1+hII)与两个坐标轴围成的矩形区域内。资本积累均衡方程式(2)表示了一条直线,此直线处于矩形区域内的线段上的点,都代表了扩大再生产公式的解,是扩大再生产优化问题的可行解。所以扩大再生产有一条可行解线段,在图中用粗线条标出。可行解线段的斜率是-1,与两个坐标轴围成等腰三角形。对于资本积累均衡方程中的状态参数(YI(t)-CII(t))取不同值的情形,可以看作是可行解线段随着参数取不同的值,可以在矩形区域内上、下平行移动;参数(YI(t)-CII(t))取值越大上移的位置就越高。矩形区域的右上顶点,是可行解线段能够上移到的最高位置,到这最高位置可行解线段就收缩成只是一个点。图1中标出了可行解线段所处的两种有一般代表性的位置。

图1 条件下的两个最优解点
在第Ⅰ部类的不变资本产出率高即(1+eI)│hI>(1+eII)│hII条件下,目标函数直线是相对陡峭的,与坐标系的横轴在第一和第二象限形成小于135度的钝角夹角,如图1所示。因而当且仅当目标函数直线向上平行移动到在可行解线段的右端点与此线段相交时,到达最高位置,从而目标函数取得最大值。所以,可行解线段的右端点(△CI(t)*,△CII(t)*)就是目标函数的最优解点。而在可行解线段上,右端点就是横坐标数值最大的点。所以最优解点的横坐标值是:

根据图1所示的此可行解线段所处的两种有一般代表性的不同位置,可以看出,可行解线段上右端点的横坐标数值是:
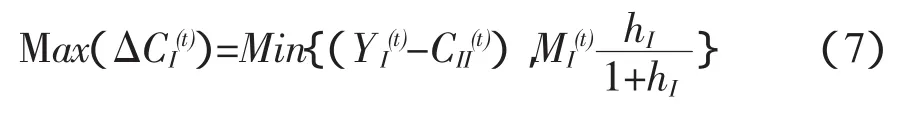
进而由于最优解点是在可行解线段上,所以横坐标与纵坐标数值之间满足资本积累均衡方程式(2),因而纵坐标数值是△CII(t)*=(YI(t)-CII(t))-△CI(t)*。用这样确定的△CI(t)*和△CII(t)*分别替换目标函数式(5)中的待定变量△CI(t)和△CII(t),就获得目标函数的最大值。
图1中还将最优解点分别放到两条边界线△CI(t)=MI(t)hI│(1+hI)和△CII(t)=MII(t)hII│(1+hII)用双向箭头线条标出。这两个双向箭头的长度是dj(t)*(当最优解点就在直线△CI(t)=MI(t)hI│(1+hI)上时,双向箭头收缩成为一个点,长度dj(t)*=0)。

而根据剩余价值使用的行为方程式(1),将双向箭头的长度dj(t)*乘一个放大系数,就得到最优解的第j部类企业所有者把本部类的剩余价值中用于个人消费的部分Mxj*。
综合以上图解法,在第Ⅰ部类的不变资本产出率高条件下,可行解线段的右端点(△CI*,△CII*)总是成为最优解点。最优解点的横坐标值△CI(t)*是待定变量△CI(t)能够取得的最大值M ax(△CI(t)),这与使用“价值系数法”求最优解的结果完全一致。[2]将以上图解法的结果归纳列成表1。
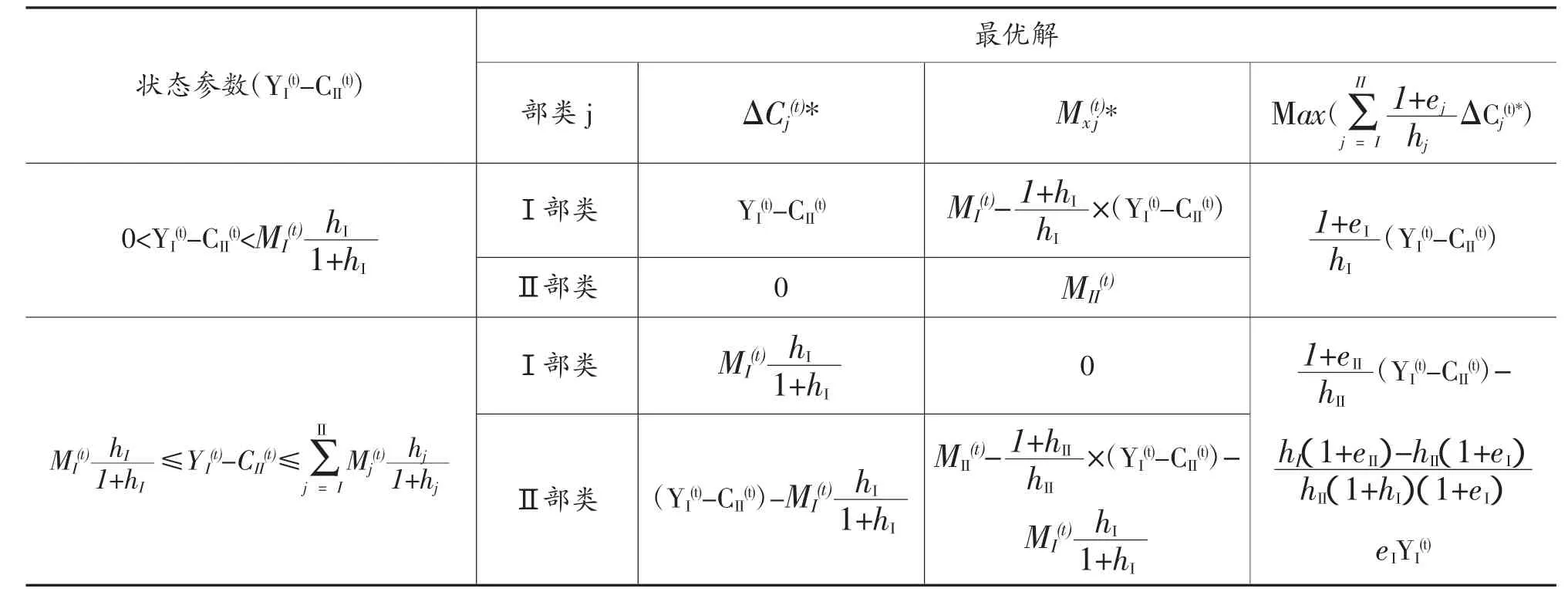
表1 在第Ⅰ部类的不变资本产出率高条件下扩大再生产的最优解
三、在第Ⅱ部类的不变资本产出率高条件下扩大再生产优化的图解法
在第Ⅱ部类的不变资本产出率高即(1+eI)│hI<(1+eII)│hII条件下,目标函数直线是相对平缓的,与坐标系的横轴在第一和第二象限形成大于135度的钝角夹角,如图2所示。
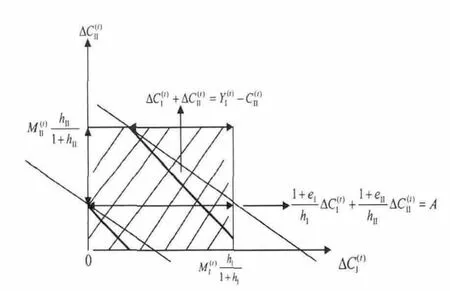
图2 条件下的两个最优解点
当且仅当目标函数直线向上平行移动到在可行解线段的左端点与此线段相交时,到达最高位置,从而目标函数取得最大值。所以,可行解线段的左端点(△CI(t)*,△CII(t)*),就是目标函数的最优解点。而左端点是可行解线段上纵坐标数值最大的点。所以最优解点的纵坐标值是:

根据图2所示的此可行解线段所处的两种有一般代表性的不同位置,可以看出,可行解线段左端点纵坐标数值是:

进而由于此交点是在可行解线段上,所以横坐标与纵坐标数值之间满足资本积累均衡方程式(2),横坐标值是△CI(t)*=(YI(t)-CII(t))-△CII(t)*。用这样确定的△CI(t)*和△CII(t)分别替换目标函数式(5)中的待定变量△CI(t)和△CII(t),就获得目标函数的最大值。
类似地,图2中还将此最优解点分别放到两条边界线△CI(t)=MI(t)hI│(1+hI)和△CII(t)=MII(t)hII│(1+hII)双向箭头标出。这两个双向箭头的长度是dj(t)*。将双向箭头的长度dj(t)*乘一个放大系数,就得到最优解的第j部类企业所有者把本部类的剩余价值中用于个人消费的部分Mx(t)j*。
综合以上图解法,在第Ⅱ部类的不变资本产出率高条件下,可行解线段的左端点(△CI*,△CII*)必定成为最优解点。最优解点的纵坐标值△CII(t)*是待定变量△CII(t)能够取得的最大值M ax(△CII(t)),这与使用“价值系数法”求最优解的结果完全一致。[2]这里要说明一下为什么使用图解法与“价值系数法”求最优解的结果能够完全一致。因为当使用图解法,哪个部类的不变资本产出率高,目标函数“等值线”就沿着可行解线段向该部类新增不变资本数值大的方向移动,直至到达此线段的端点,所以图解法倾向于使不变资本产出率高的那个部类新增不变资本取得最大值。而每个部类的不变资本产出率就是“价值系数法”当中的价值系数,“价值系数法”是使价值系数大的那个部类新增不变资本取得最大值。所以,用两种方法求最优解的结果完全一致。
将以上图解法的结果归纳列成表2。
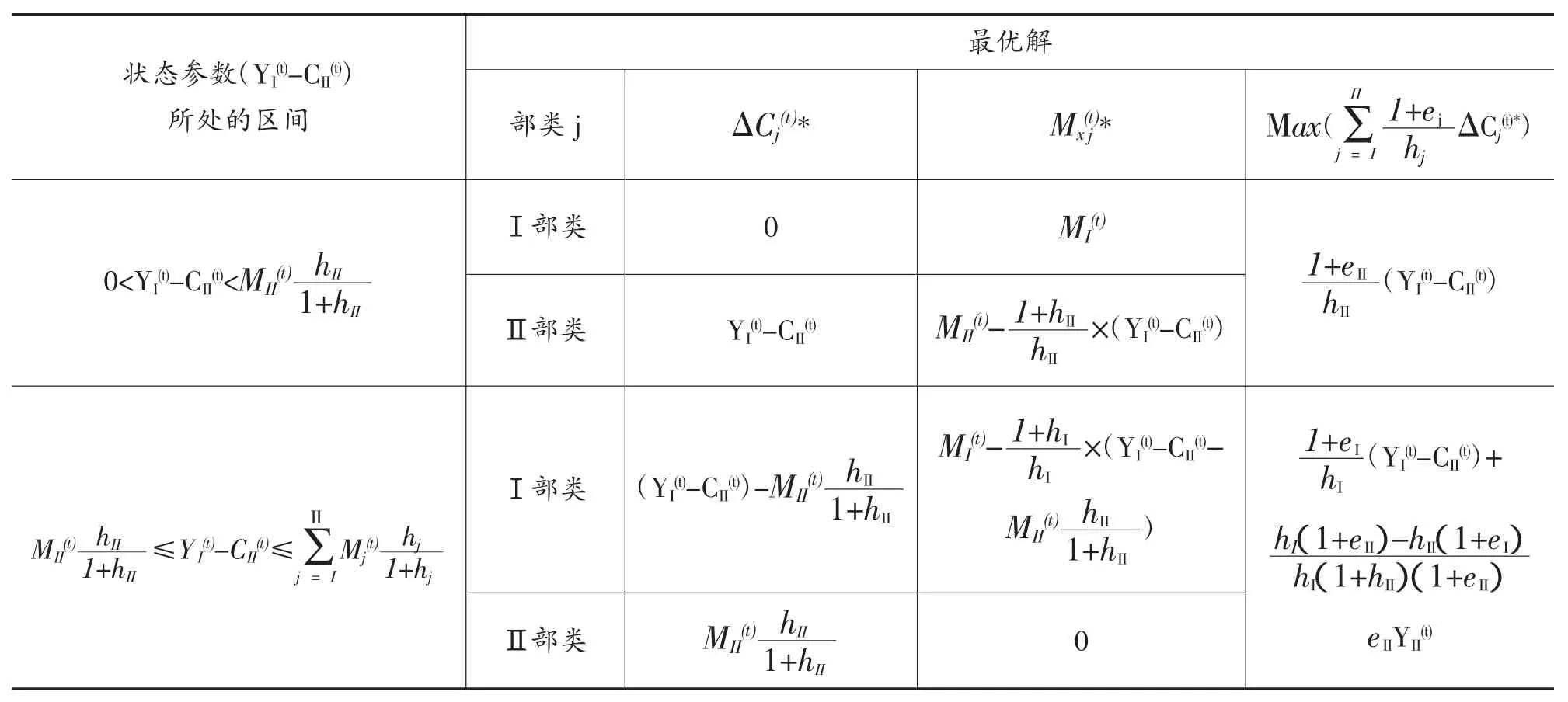
表2 在第Ⅱ部类的新增不变资本价值系数大的条件下扩大再生产的最优解
四、借助《资本论》的举例计算最优解
下面借助《资本论》第2卷第21章所举的第一例,[5]对以上给出的社会扩大再生产优化的图解法的最优解进行计算验证。此例设定两个部类结构参数是:hI=4倍,hII=2倍,eI=eII=100%,说明一般情形下两大部类的扩大再生产过程。该例是本文所分析的第Ⅱ部类的新增不变资本价值系数大(即(1+eI)│hI<(1+eII)│hII)的条件。引用该例中的第2年(起始年份的下一年)数据,此年CI(t)=4400,VI(t)=MI(t)=1100,CII(t)=1600,VII(t)=MII(t)=800。此年扩大再生产中的(YI(t)-CII(t))=600,它的数量所处区间是MII(t)hII│(1+hII)≤YI(t)-。运用图解法计算两大部类扩大再生产的最优解,根据表2,得到:△CI(t)*=66.7,△CII(t)*=533.3,IMx(t)*=1016.6,IIMx(t)*=0。目标函数最大值计算出的最优解与运用单纯形法、“价值系数法”获得的结果完全相同。[1][2]
