顾及邻域变化的图斑群合并方法研究

翁 杰，王志鹏，唐 皓，郭庆胜

(1.北京数字政通科技股份有限公司，北京100082;2.中国科学院电子学研究所，北京100190;3.武汉大学资源与环境科学学院，湖北武汉430079)

一 、引 言

土地利用数据是一种具有复杂的空间关系和语义层次结构的多边形类型数据，这种特殊的专题数据的自动综合需要考虑拓扑、几何和语义等多方面的知识［1］。作为土地利用数据自动综合非常重要的部分，图斑群自动综合的研究受到了国内外学者们的广泛关注。比较具有代表性的研究成果有如下几类:郭庆胜等研究了图斑群的渐进式合并策略［2］;艾廷华等从计算几何的角度研究了图斑合并算子［3-6］;Peter等提出了一种矢量和栅格模型结合的图斑群合并方法［7］;还有一些学者从拓扑一致性及自动综合规则应用方面研究了图斑群的自动综合问题［8-9］。这些研究所关注的对象主要是符合合并条件的图斑，但是土地利用数据具有全覆盖、无重叠、无缝隙的特点，任意两个空间上不相邻的图斑多边形的合并需要填充中间的“桥梁区域”，必然会对其邻域图斑造成影响，并产生新的空间冲突，如重叠。这种空间冲突的解决往往伴随着某一图斑被切割，即面积减少，可能又会产生新的冲突(面积过小)，造成同一区域反复进行综合操作。因此，图斑群合并的关注对象还应包括待合并图斑的邻域图斑。

目前，图斑群自动综合的研究主要集中于参与合并过程的图斑［2-6］，综合考虑合并区域及其邻域图斑变化情况的研究成果还非常少。本文研究了一种顾及合并区域及其邻域图斑变化的图斑群合并方法，有效地控制了邻域图斑的变化，避免了新的空间冲突的产生，优化了图斑群合并效果。

二、图斑群合并的基础变量定义

土地利用数据综合过程中的图斑群合并对象主要包括两类:面积过小导致在目标比例尺下不易辨识的图斑;距离过近导致在目标比例尺下无法区分的图斑。针对这两类图斑，至少需要设置两类自动综合阈值，即最小面积阈值和最小距离阈值，最小面积阈值与地类重要性相关且呈现不一致，最小距离阈值适用于所有地类。

设D为目标比例尺下图斑间的最小距离阈值，对任意图斑 Pi，定义如下:①Pi的面积表示为S(Pi);②Pi所属地类在目标比例尺下的最小面积阈值表示为Si;③Pi的权属单位和地类名称分别表示为O(Pi)和L(Pi);④Pi的几何多边形区域表示为Poly(Pi);⑤Pi和任意图斑多边形Pj之间的最小距离表示为D(Pi，Pj);⑥若S(Pi)≥Si，则分别称Pi和Poly(Pi)为大图斑和大多边形，反之则为小图斑和小多边形;⑦图斑多边形之间的差集表示为I(Pi，Pj)=Poly(Pi)－Poly(Pj)，图斑多边形Pi与图斑多边形集合P之间的差集I(Pi，P)=Poly(Pi)－(Poly(P1)+Poly(P2)+…+Poly(Pn))，其中 P={P1，P2，…，Pn};⑧Pi的语义邻近图斑集合表示为SNS(Pi)={Pm，Pn，…，Pk};⑨对任意 Px∈SNS(Pi)，连通图斑Pi与Px的区域(桥梁多边形)表示为Brx(Brx可能为多外环的复杂多边形)，则与语义邻近图斑集合SNS(Pi)对应的桥梁多边形集合Br(Pi)={Brm，Brn，…，Brk}，与Br(Pi)产生重叠的图斑集合定义为Ba(Pi)={Bam，Ban，…，Bak}，其中任意Bax∈Ba(Pi)为与桥梁Brx重叠的图斑集合。

三、图斑群合并的方法分析

1.聚合方法

(1)聚合图斑的邻域图斑状态分类

若 D(Pi，Pj)＜D，且 O(Pi)=O(Pj)，L(Pi)=L(Pj)，则 Pj∈SNS(Pi)。对任意 Bak∈Bax∈Ba(Pi)，I(Bak，Brx)=Poly(Bak)－Poly(Brx)，表示某一邻域图斑与桥梁多边形之间的差集。

图1(a)、(b)、(c)为图斑合并过程中邻域图斑状态出现的3种情况的简化图。设P0和P1表示将要进行聚合的图斑，P2表示邻域图斑，阴影区域表示连通P0和 P1的桥梁区域，I(Bak，Brx)可能存在3种状态:

1)I(Bak，Brx)= Φ，如图1(a)所示，P2完全被桥梁区域覆盖。

2)I(Bak，Brx)≠ Φ，且 I(Bak，Brx)为简单多边形，如图1(a)所示，桥梁区域覆盖P3的一部分，且P3未被覆盖的部分为简单多边形。

3)I(Bak，Brx)≠ Φ，且 I(Bak，Brx)为复杂多边形，即由多个外环组成，如图1(b)和图1(c)所示，P2被桥梁区域隔断为包含两个外环的复杂多边形，其中图1(b)较图1(c)中，P2被P0、P1和桥梁区域包围的部分面积更大，假设图1(b)和图1(c)中P2被包围的部分分别为大多边形和小多边形，将对这两种情况采用不同的处理方式。

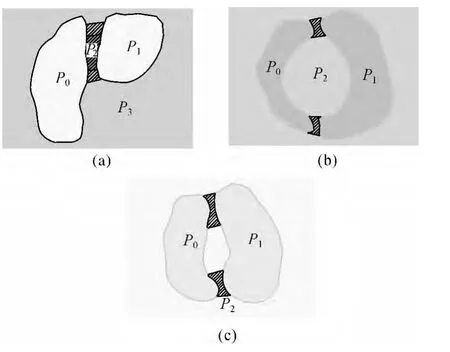
图1

将I(Bak，Brx)视为简单多边形的集合，简写为I={I1，I2，…，In}，其中 In∈I为一个简单多边形(有且仅有一个外环)，集合I中大多边形和小多边形集合分别定义为IB和IS，其中IB⊆I，IS⊆I，且IB∩IS=Φ。IB和IS的累计面积和分别为S(IB)和S(IS)。

结合Bak，以及IB和IS，可以得出如下8种组合:①S(Bak)＞Sx，IB=Φ，IS=Φ;②S(Bak)＞ Sx，IB≠Φ，IS=Φ;③S(Bak)＞ Sx，IB ≠Φ，IS ≠Φ 且S(IS)＞Sx;④S(Bak)＞ Sx，IB ≠Φ，IS ≠Φ 且 S(IS)＜Sx;⑤S(Bak)＞ Sx，IB=Φ，IS ≠Φ 且 S(IS)＞Sx;⑥S(Bak)＞ Sx，IB=Φ，IS≠ Φ 且 S(IS)＜Sx;⑦S(Bak)＜ Sx，IS=Φ;⑧S(Bak)＜Sx，IS ≠Φ;

其中，组合①⑥是不可能出现的结果，本文采用的处理方法有效避免了组合③⑤出现，后文将进行详细解释。

(2)图斑处理方法

为了使局部区域内的图斑群合并效率更高，并且不产生新的空间冲突，本文处理图斑Bak的两条基本规则是:①对大图斑Bak∈Bax，在维持其大图斑状态的基础上进行拓扑求差，并且Bak的面积变化小于Sx;②对任意图斑Bak∈Bax，拓扑求差后不允许产生新的小图斑，即，若IS≠Φ，且S(IS)＜Sx，对IS中的小图斑进行融合。

任意Brx∈Br(Pi)可能为复杂多边形，将Brx分解为独立的简单多边形集合 BRS={BRS1，BRS2，BRS3，…，BRSn}，任意 BRSn∈BRS，且 BRSn≠Φ，满足I(BRSn，Brx)=Φ。BRS与Bax中的元素可能存在多对多的关系。以简单多边形作为主体，依次与Brx进行渐进式求差，若存在BRS1⊆BRS和BRS2⊆BRS，满足关系 BRS2－BRS1={BRSj}，求差后，得到的小多边形集合分别为IS1和 IS2，且满足关系:①IS1⊆I(Bak，BRS1)，IS2⊆I(Bak，BRS2);②S(IS1)＜Sx，S(IS2)＞Sx，则称 BRSj为临界多边形。对大图斑Bak，临界多边形的产生使得对Bak的操作结果违背原则①，应将其从BRS中剔除，因此组合③⑤是不可能出现的结果。

综合以上分析，对 Pi，Px∈SNS(Pi)，BRS(已剔除临界多边形)及Bak∈Bax∈Ba(Pi)在聚合过程中的操作规则总结如下:

1)若 Bak满足组合②:合并 Pi、Px和 BRS，并用合并结果替换Pi的几何形体，修改Pi的属性;取任意IBj∈IB替换Bak的几何形体，修改Bak的属性;为IB－{IBj}中的所有简单多边形对象赋属性，以新图斑的形式写入土地利用数据库;从数据库删除Px的记录。

2)若 Bak满足组合④:对 Pi、Px、BRS，以及 IB的操作同②;对任意ISj∈IS进行融合操作，融合方法描述见下节。

3)若 Bak满足组合⑦:对 Pi、Px、BRS的操作同②;从数据库中删除Bak的记录。

4)若 Bak满足组合⑧:对 Pi、Px、BRS的操作同②;对任意ISj∈IS进行融合操作。

根据以上分析，对图1(a)、(b)、(c)3种情况的处理结果分别如图2中(a)、(b)、(c)所示。

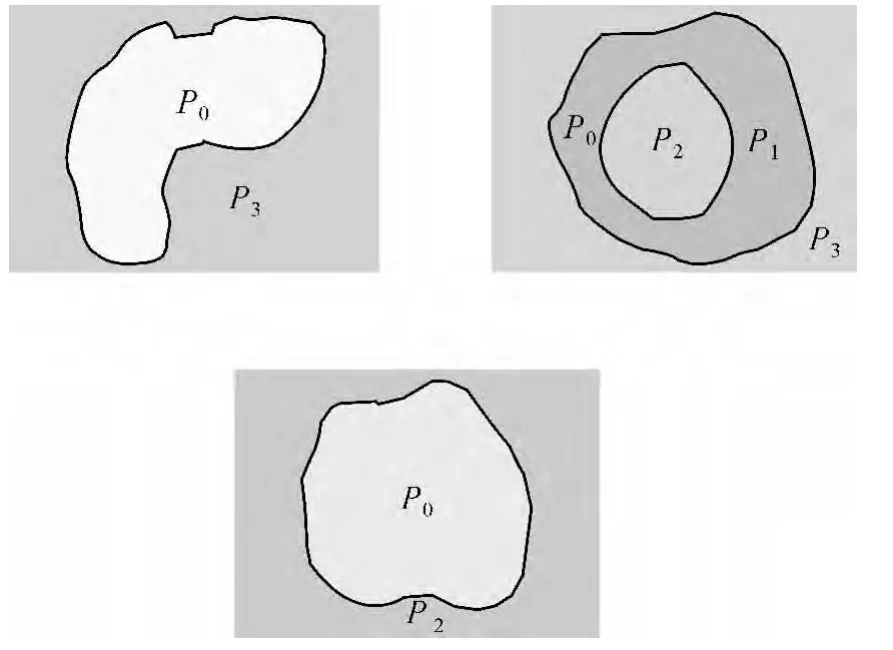
图2

2.融合方法

设任意图斑Pi的拓扑相邻图斑集合NS(Pi)={P1，P2，…，Pn}，n≠i。任意 Pj∈NS(Pi)满足:①O(Pi)=O(Pj);②Pj与Pi之间存在公共边界(线)。设NS(Pi)中与 Pi同父类的图斑集合为NSF(Pi)，则 NSF(Pi)⊆NS(Pi)。

定义结点为图斑多边形之间公共边界的起始点和终止点。将小图斑Pi的骨架线进行修正，使之与每个结点之间都存在一条分支连通，用修正的骨架线剖分Pi得到剖分子集CS(Pi)［3-6］。融合知识主要遵循3个原则:

1)若 NSF(Pi)≠Φ，CS(Pi)优先合并到 NSF(Pi)中，以尽可能减少二级地类的总面积变化量(本文直接作用于三级地类对象)。

2)以最长公共边界作为判断依据，将CS(Pi)中的对象合并到NS(Pi)或NSF(Pi)中。

3)CS(Pi)与NSF(Pi)或NS(Pi)合并后，合并新的NSF(Pi)或NS(Pi)中同类并且拓扑相邻的图斑对象。

设 P0为小图斑，NS(P0)={P1，P2，P3，P4，P5}，P0的剖分子集 CS(P0)={C1，C2，C3，C4，C5}，如图3所示。可能出现如下合并结果:①若NSF(P0)=Φ或NSF(P0)=NS(P0)，且NS(P0)中不存在同类图斑，合并结果如图4(a)所示;②若NSF(P0)≠Φ，且NS(P0)－NSF(P0)={P4}，NS(P0)中不存在同类图斑，合并结果如图4(b)所示;③若NSF(P0)≠Φ，NS(P0)－NSF(P0)={P4}，且 P3与 P5属于同一地类，合并结果如图4(c)所示。

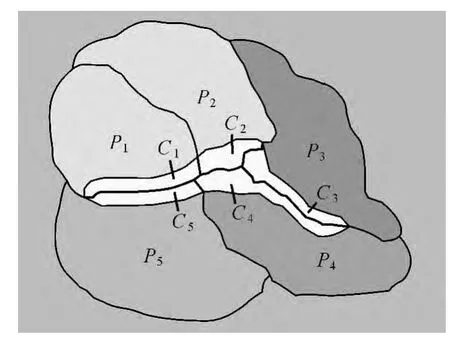
图3 P0的剖分子集示意

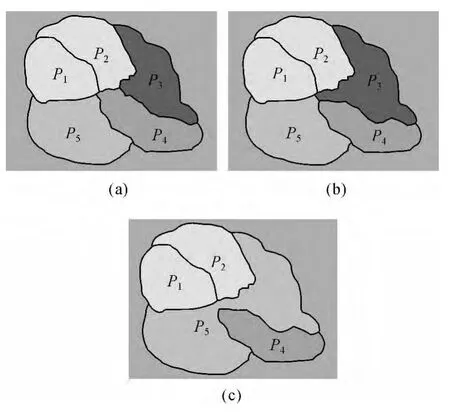
图4

四、图斑群合并试验

本文的试验数据为某地1∶10 000土地利用数据，试验数据中二级地类分布的特点是:林地面积较大，城乡建设用地以小面积地块为主呈局部密集分布，其他建设用地和农田水利用地分布零散且面积小。本试验采用的参数如下:

1)最小图斑间距D为40 m。

2)最小面积阈值设置如下:耕地、园地的最小面积阈值为12 500 m2，林地、牧草地和自然保留地最小面积阈值为22 500 m2，其他农用地最小面积阈值为5000 m2，城乡建设用地、交通水利用地、其他建设用地、水域和滩涂沼泽最小面积阈值为3000 m2。

图5和图6所示分别为原始试验数据和进行图斑群合并后的试验结果，在试验结果中小面积图斑均被删除，试验前后的图斑总数分别为3960和1020。从图中可以看出，试验前后的地类大致分布没有明显变化，试验结果较好地维持了地类的整体分布情况。

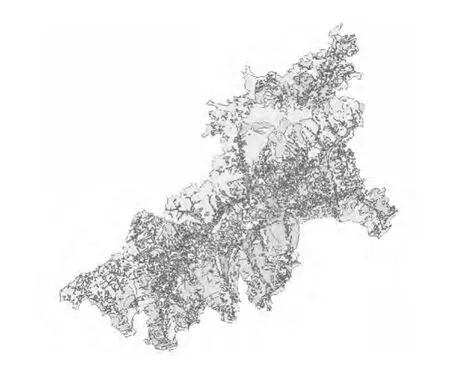
图5 原始数据

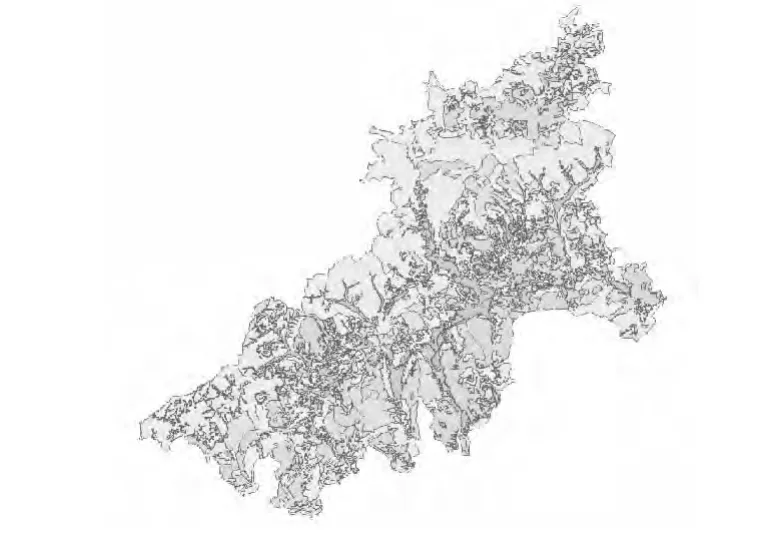
图6 试验综合结果

五、结束语

本文提出的顾及邻域图斑变化的图斑群合并方法，有效避免了图斑群合并过程中新的空间冲突产生，提高了合并效率，试验结果较好地维持了原始数据的地类分布情况，并且有效减少了图斑数量。本文的研究成果能够为地图生产提供一定的理论和技术支持，具有较强的实用性。

［1］GALANDA M.Automated Polygon Generalization in a Multi Agent System［D］.Switzerland:University of Zurich，2003.

［2］郭庆胜，王晓妍，刘纪平.图斑群合并的渐进式方法研究［J］.武汉大学学报:信息科学版，2012，37(2):220-223.

［3］艾廷华，刘耀林.土地利用数据综合中的聚合与融合［J］.武汉大学学报:信息科学版，2002，27(5):486-492.

［4］AI T H，VAN Oosterom p.A Map Generalization Model Based on Algebra Mapping Transformation［C］∥Proceedings of the 9th ACM-GIS.Atlanta:［s.n.］，2001:21-27.

［5］翁杰，郭庆胜，王晓妍，等.一种改进的图斑合并算法［J］.武汉大学学报:信息科学版，2012，37(9):1116-1119.

［6］BADER M，WEIBEL R.Detecting and Resolving Size and Proximity Conflicts in the Generalization of Polygonal Maps［C］∥Proceedings of the 18th International Cartographic Conference.Stockholm:［s.n.］，1997:1525-1532.

［7］PETER B，WEIBEL R.Using Vector and Raster-based Techniques in Categorical Map Generalization［C］∥Proceedings of Third ICA Workshop on Progress in Automated Map Generalization.Ottawa:［s.n.］，1999:12-14.

［8］李精忠，艾廷华.多尺度土地利用数据库构建过程中的拓扑一致性维护［J］.测绘通报，2011(8):32-35.

［9］牛方曲，甘国辉，程昌秀，等.矢量数据综合规则表达与实现方法——以土地利用数据综合为例［J］.地球信息科学学报，2009，11(4):421-427.