一种基于智能手机成像的立体量测方法
2015-12-11徐殿成陈智勇赵双明
徐殿成,陈智勇,赵双明
(武汉大学遥感信息工程学院,湖北武汉430079)
一、引 言
近年来,非量测型相机越来越广泛地应用于近景摄影测量的各个领域。而智能手机的相机作为一种价格便宜、使用方便、成像效果尚佳的非量测型相机,鲜有人使用它采集的影像来作立体量测。虽然手机相机使用的是定焦镜头,但在成像过程中不能精确设置相机主距,其自动聚焦特性会影响到主距的大小。因此,有必要先对其成像参数的稳定性进行验证[1]。
近景摄影测量过程中常出现大角度、主光轴不平行等现象,这与航空摄影测量保持规则的竖直平行摄影有所不同。大角度带来的影像畸变较大、左右像片姿态差别较大,从而导致定向角元素过大及初值计算精度不高[2-3],使用传统的连续法相对定向常会出现迭代过程不收敛的情形,而相对定向的直接解法,不需要初值,通过像点坐标即可直接解算出相对定向元素。立体像对的相对位置关系确定后,即可利用前方交会解算待求点的物方坐标。
二、手机相机成像特征
1.手机相机
随着现代科学技术的飞速发展,手机相机镜头的成像能力在逐渐提高。由于手机的整体发展趋势是更轻更薄,无法从增大传感器感光面积这方面来提高成像质量,只能通过改变图像传感器的自身结构来实现。手机相机的成像传感器从传统式CMOS到背照式CMOS再到堆栈式CMOS,成像质量发生了质的飞跃。市面上的主流品牌手机都相继推出高品质的手机相机,如诺基亚、索尼、三星、苹果等,其最高像素已达4100万像素。
2.手机相机成像特征
由高斯成像原理(1/F=1/u+1/v),焦距F一定时,物距u发生变化,像距v也相应发生变化。相机主距f为摄影物镜的后节点到像平面的垂直距离,即等于像距v。绝大部分手机都使用定焦镜头,仅能自动调焦而不支持手动调焦。成像过程中,根据不同成像距离自动调节像距,因而主距并不固定,但是,由于手机成像感光元器件尺寸非常小,其镜头实际焦距也非常小(约相当于全画幅相机的1/8)。因而,即使在拍摄距离相当近时,物距也已远大于像距(类似于无穷大),此时,像距(相机主距)可认为近似等于焦距。
对于手机相机来说,除了主距外,像主点在像片中心坐标系中的偏移量及镜头的光学畸变等因素,也会使量测的像点坐标产生误差。
3.手机相机标定
为验证手机相机成像参数的稳定性,使用笔者所在单位的室内三维检校场,设计了一组标定试验。试验所采用的手机是索尼Lt26ii,该手机相机搭载了Exmor R背照式CMOS传感器,感光元件大小为1/3.2 英寸,光圈大小为 F2.4,有效像素 1200 万像素。
对室内检校场由远及近进行拍摄,得到了6组不同距离成像时手机相机的各项成像参数,像幅大小均为4000像素×3000像素,如图1所示。

图1 不同拍摄距离对手机相机成像参数进行标定
标定过程中,通过半自动提取像片上三维检校场的标志点,获取其像素坐标,而其三维坐标已知,可基于DLT和后方交会原理[4-5],解求出相机的内方位元素和畸变参数。得到的6组标定结果见表1。
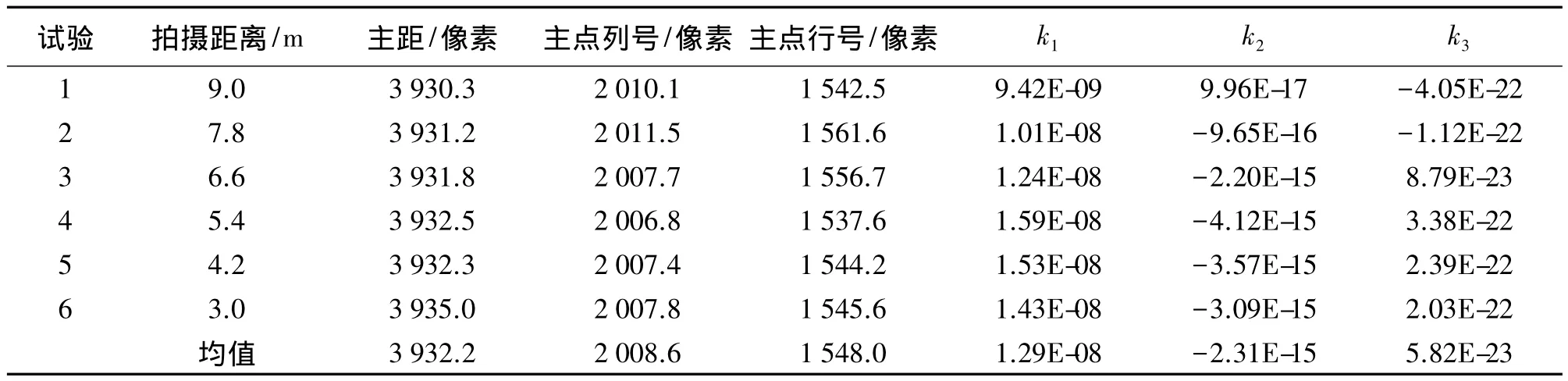
表1 不同拍摄距离获取的手机相机成像参数
从表1中可以看出,手机相机的主距随着拍摄距离不同而发生的变化非常小,其平均相对误差仅0.03%。其他成像参数,如像主点坐标及畸变差,随着距离的变化也是相对稳定的。
此外,手机相机镜头的物理焦距一般在4 mm左右,相当于全画幅相机的35 mm镜头(等效焦距)。当拍摄距离在3 m左右时,手机成像的物距近似是像距的千倍,而全画幅相机在此距离则不足百倍,即相对于全画幅相机而言,手机相机的超焦点距离要近得多。因此,就成像清晰范围(拍摄距离)这一指标而言,手机相机的芯片比数码相机有绝对的优势。
三、手机像对的立体量测
在分析手机成像的立体量测方法时,仍选用室内检校场作为试验对象。量测过程中,仅将其标识点作为待求点,解算在自定义物方坐标系中的坐标值(量测值)。精度验证时,将标识点在检校场局部坐标系中的坐标值视作真值,以进行比较分析。将采集的左、右像片构成单独像对,按下述方法实现立体量测。
1.影像的畸变校正
镜头的光学畸变使所量测的像点坐标会产生误差,因此须先对其进行校正[6]。由检校得出了相机的内方位元素(x0,y0,f)和畸变参数 k1、k2、k3,对手机相机采集的像对进行畸变矫正(只考虑径向畸变),当像平面坐标为(x,y)时,数码相机的畸变差可以表示为
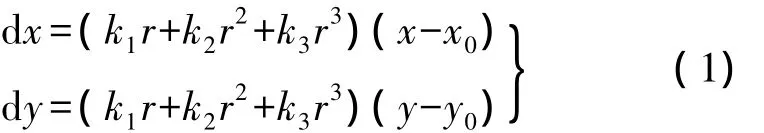
其中,dx、dy为畸变差,与像平面坐标和径向距离r有关;r=(x-x0)2+(y-y0)2。经畸变校正之后,手机影像的几何畸变残差小于0.5像素。
2.相对定向直接解
相对定向的目的是为了恢复构成立体像对的两张像片的相对方位,建立被摄物体的几何模型,从而使同名光线对对相交[7]。当倾斜摄影中的倾角近似值或影像的内方位元素未知时,须采用相对定向的直接解法[8]。
立体像对相对定向的数学模型是相应的摄影光线与基线应满足共面条件
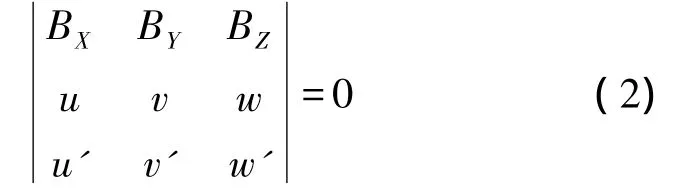
相对定向中假定左方影像是水平的,其外方位元素均视作零值。左片的像空间坐标为(x,y,-f),由于旋转矩阵为单位阵,可直接得到左片像空间辅助坐标(u,v,w)。而由相对定向得到的角元素(φ,ω,κ)构成了右片相对于左片的旋转矩阵R'。右片的像空间坐标(x',y',-f'),可通过转换得到其像空间辅助坐标(u',v',w')。
将式(2)展开,整理得
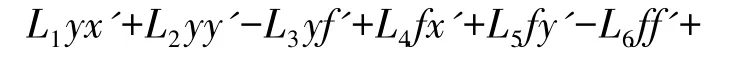
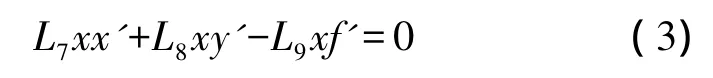
等式两边除以L5,得
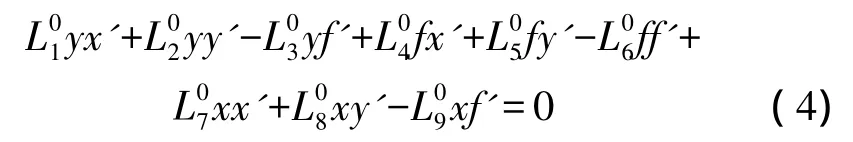
在参数解算过程中,由于旋转矩阵R'本身是一个正交矩阵,它的9个元素满足正交矩阵特有的一系列函数关系,因此可将这些关系式代入式(4)进行消元、变形,并最终得到计算基线分量和旋转矩阵R'的公式[3],进而反算出相对定向的3个角元素。
3.前方交会
在大倾角的近景摄影测量中,由于上下视差与左右视差同时存在,点投影系数法已不够严密。利用前方交会的严密解法[9],将共线条件方程整理可得
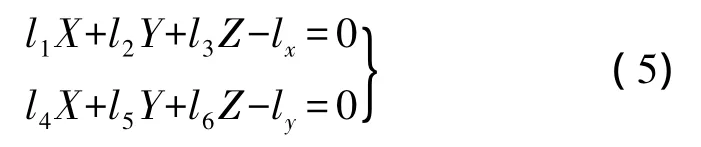
由相对定向元素和同名像点坐标,依式(5)可以解算出各待定点的物方坐标。
4.立体像对的光束法平差
通过相对定向可确定立体像对的相对位置关系,得到右片相对于左片的外方位元素;利用空间前方交会,得到待求点的物方坐标。但为了提高量测精度,可进一步作单独像对的光束法平差[10]。
平差过程中,将同名点的像点坐标(x,y)作为观测值,外方位元素(XS,YS,ZS,φ,ω,κ)和待求点的物方坐标(X,Y,Z)都作为未知数,通过前面获取的相对定向元素和物方坐标为其提供初值,解求各未知数的改正数,以优化相对定向结果和待求点的物方空间坐标。光束法误差方程式可简单表示为

在确定模型系数前,该平差过程都是基于相对定向的,基线分量BX视作定值,其改正数为零。因为没有控制点,且内方位元素由标定过程确定,故误差方程中各系数阵为
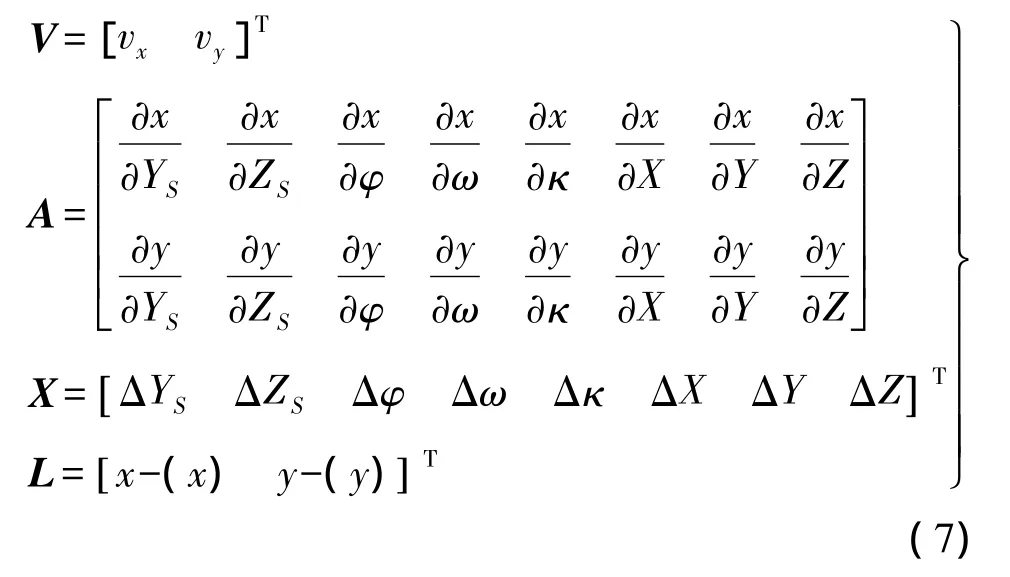
在左右像片上取n对同名像点,可列4n个方程,解算3n+5个未知数(5个相对定向元素和n个同名像点的物方坐标)的改正数,由此可知误差方程式各矩阵阶数是 V4n×1、A4n×(3n+5)、X(3n+5)×1、L4n×1,其法方程未知数系数矩阵的结构如图2所示。
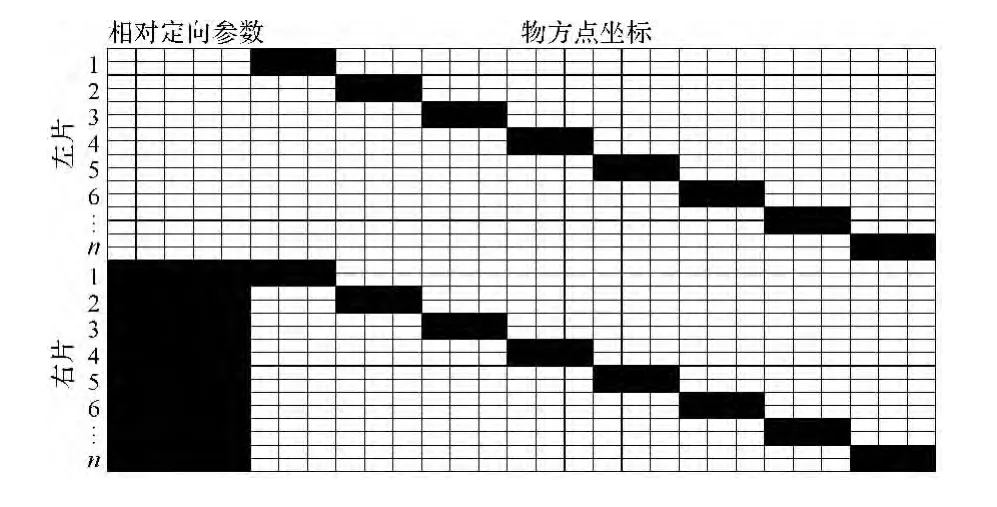
图2 法方程式未知数系数矩阵
为了确定模型系数,任意选取立体像对中的两个标识点。计算这两点在自定义物方坐标系中的距离S1及其在检校场局部坐标系中的距离S2,这两个距离的比值S2/S1即为模型比例系数,利用该系数,修正标识点在自定义物方坐标系中的坐标值。此时,各个标识点在自定义物方坐标系和检校场局部坐标系中的三维坐标,虽数值大小不同,但尺度大小完全相同。
四、试验分析
通过手机相机采集的左、右像片构成立体像对,选取数目适量、分布均匀的同名像点(均为检校场的标识点),图3所示为第一组试验。

图3 手机像对立体量测过程中选取的同名点
试验计算过程中,相对定向直接解得到相对定向元素(即右片相对于左片的外方位元素),前方交会得到了标识点的物方坐标。为提高量测精度,将相对定向元素和物方坐标作为初值,进行光束法平差,并确定了模型系数。表2中列出了两组试验(不同的立体像对)相对定向直接解法的外方位元素和光束法平差优化后的外方位元素。

表2 光束法平差前后右片相对于左片的外方位元素
经过光束法平差及模型系数解算后,各标识点在自定义物方坐标系和检校场局部坐标系中有尺度大小相同的三维坐标,即任意两标识点在自定义物方坐标系中的距离与它们在检校场局部坐标系中的距离是相等的。因此,可以利用点与点之间的距离来分析测量精度,避免坐标转换带来的中间误差。
选取其中一个标识点作为基点,计算其他标识点到基点的距离。在自定义物方坐标系中,该距离为量测值,记为 di(i=1,2,…,n-1)。在检校场局部坐标系中,该距离为真实值,记为d'i(i=1,2,…,n-1)。统计各个量测值与真实值的差值Δdi(i=1,2,…,n-1),并通过其各项指标来分析手机相机的量测精度,见表3。
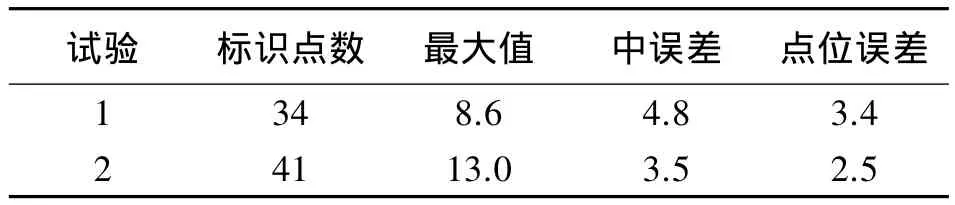
表3 量测值与真实值差值Δdi的各项精度指标 mm
由以上两组结果可以看出,不论是距离Δdi的中误差还是点位误差,都表明手机的测量精度足够用于某些不需要很高精度的摄影测量工作。
五、结束语
本次试验是首次尝试使用手机相机这种非量测相机来实现立体量测功能,从试验结果可以得出如下结论:①常规成像距离范围内,手机相机虽然有自动聚焦功能,但其成像参数相对稳定,且小芯片在近景摄影测量中具有优势;②相对定向直接解法,克服了大倾角且无控制点的场景,不需要设定初值,回避了传统相对定向方法中的迭代过程,直接有效地解算出了像对的相对位置关系;③利用光束法平差,优化了相对定向结果,提高了待求点的物方坐标的精度;④利用检校场控制点的坐标真值,通过距离的差值间接分析了手机相机的量测精度,满足测量要求。总之,即使手机相机测量的误差和专业测量相机相比仍显得比较大,但其具有携带方便、使用简单,且成像质量较好的优势,在某些摄影测量应用中仍然是取代数码相机完成摄影测量任务的较好选择。
[1]张本昀,吴晓明,喻铮铮,等.非量测型相机检校及可靠性研究[J].测绘科学,2008,33(4):84-86 .
[2]杨立君,马明栋,苗立志.非量测相机近景数字影像相对定向方法研究[J].大地测量与地球动力学,2012,32(4):135-138.
[3]陈义,陆珏,郑波.近景摄影测量中大角度问题的探讨[J].测绘学报,2008,37(4):458-463.
[4]佟书泉,王东,任忠成,等.基于二维DLT方法的普通数码相机检校[J].测绘通报,2007(9):14-16.
[5]王冬,冯文灏,卢秀山,等.基于多片空间后方交会的CCD 相机检校[J].测绘科学,2008(4):64-66.
[6]李天子,郭辉.非量测数码相机的影像纠正[J].测绘通报,2006(10):59-61.
[7]张永军,张勇.大重叠度影像的相对定向与前方交会精度分析[J].武汉大学学报:信息科学版,2005,30(2):126-130.
[8]张祖勋,张剑清.数字摄影测量学[M].武汉:武汉大学出版社,2012.
[9]张剑清,潘励,王树根.摄影测量学[M].武汉:武汉大学出版社,2012.
[10]冯文灏.近景摄影测量——物体外形与运动状态的摄影法测定[M].武汉:武汉大学出版社,2002.
