特长隧道贯通误差预计方法研究
2015-12-11付宏平郭际明张正禄
付宏平,郭际明,张正禄
(1.中铁第一勘察设计院集团有限公司,陕西西安710043;2.武汉大学,湖北武汉430079)
一、引 言
隧道施工的特点要么是从两个洞口相向开挖,要么是从几个洞口(包括横洞、斜井、竖井、平行导坑)开始,深入到线路中线位置后,再沿线路中线相向开挖,即目前普遍采用的“长隧短打”的施工方法。无论哪种施工方法,隧道贯通误差均是评估隧道施工建设质量的一个重要指标,尤其是横向贯通误差和高程贯通误差。
目前,国内特长隧道工程已经很多,如已建成通车的石太客专太行山隧道,全长27.839 km,是目前国内建成通车的最长铁路隧道。正在修建的兰渝线西秦岭特长隧道是目前国内第二长大铁路山岭隧道,隧道全长28.2 km;西格二线关角特长隧道是目前国内最长的铁路山岭隧道,隧道全长32.645 km,其贯通误差特别值得关注。
现有《高速铁路工程测量规范》(TB 10601—2009)中对特长隧道(20 km及以上)贯通误差未作明确规定,而20 km及以上特长隧道已越来越多。如何进行特长隧道控制网的设计,如何预计其贯通误差影响值的大小,需要研究出一个切实可行、操作简便的方法。
二、特长隧道贯通误差预计方法研究
1.经典方法
以前见诸各类文献的隧道贯通误差预计传统方法(经典方法),主要包括导线法、误差来源分析法、权函数法。
(1)导线法
导线法是洞外、洞内控制测量所引起隧道横向贯通误差的一种近似预计方法。过去洞外平面控制采用地面三角形网、导线网,而洞内只能用导线或导线网,此法是选择最靠近隧道中线的一条线路(如图1中的J-1-2-3-4-C)作为导线,用下述导线公式预计横向贯通误差的影响值
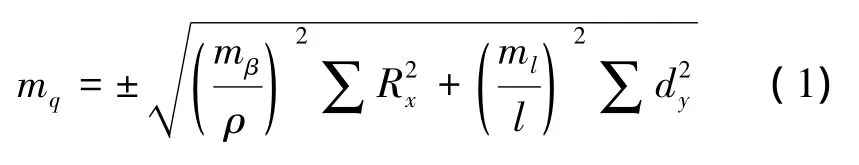
式中,mβ为测角中误差为最弱边相对中误差;为导线点至贯通面垂直距离的平方和;为导线边在贯通面上投影长度的平方和。
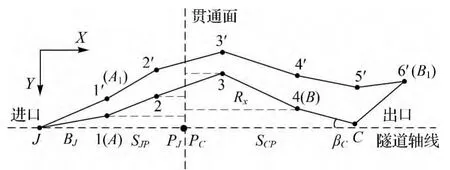
图1 导线法计算贯通误差影响值示意图
由于洞外控制测量不再采用地面三角形网、导线网,该方法对洞外控制网不再适用,但仍可用于预计洞内控制测量所引起的隧道横向贯通误差。该方法计算简单,未考虑平差后的精度增益,预计的值偏大、偏安全。
(2)误差来源分析法
《铁路工程测量规范》(TB 10101—2009)及《高速铁路工程测量规范》(TB 10601—2009)中洞外GPS平面网测量误差对隧道横向贯通的影响,采用下式预计
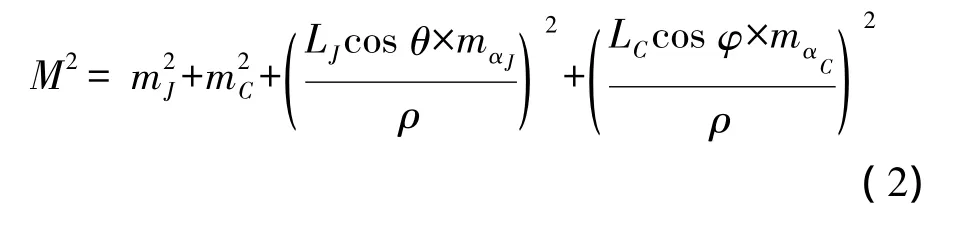
式中,mJ、mC为进、出口GPS控制点的Y坐标误差;LJ、LC为进、出口GPS控制点至贯通点的长度;mαJ、mαc为进、出口GPS联系边的方位中误差;θ、φ为进、出口控制点至贯通点连线与贯通点线路切线的夹角。
后两项也可以由下式算得
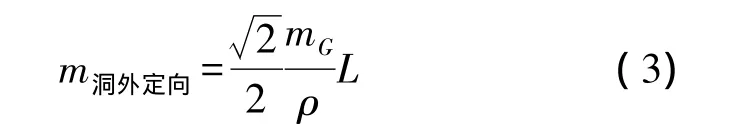
式中,mG为GPS测量定向联系边方向误差,单位为(″),为隧道设计时的先验值,ρ=206 265。
该方法使用了隧道两端洞口定向点点位误差和定向边坐标方位角中误差,这些值可以事先设计。因此,该方法适合在控制测量开始前对隧道贯通误差进行预计。
(3)权函数法
权函数法是隧道贯通误差预计严密的公式,按照隧道洞外控制网的验后单位权中误差和其坐标协因数阵来计算隧道贯通中误差,如图2所示。
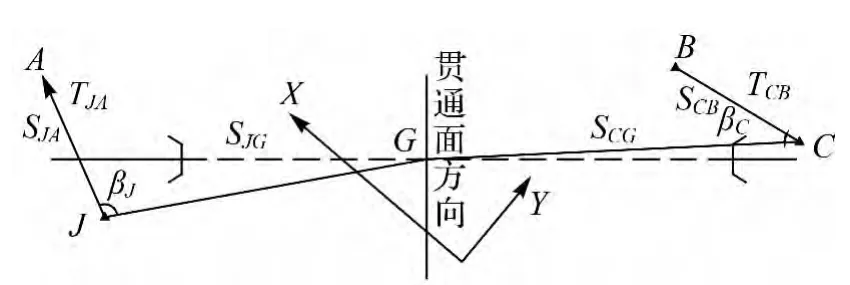
图2 权函数法计算贯通误差影响值示意图
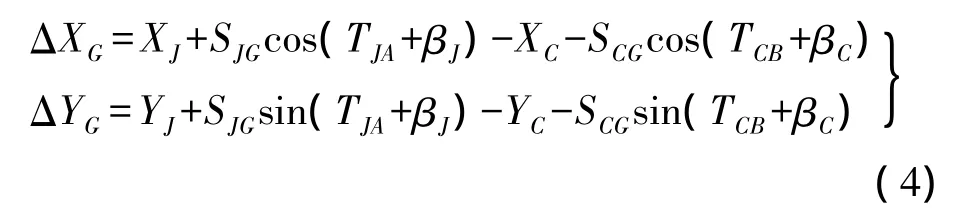
由平差理论,按求未知数的函数权倒数方法,在不考虑 SJG、SCG、βJ、βC的误差时,对上两式微分并整理得到关于ΔXG、ΔYG的权函数式(推导略)。写成矩阵形式,按协因数传播律得
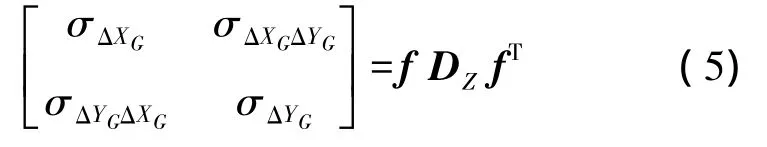
对于直线隧道,当隧道轴线为X轴时,则σΔXG为纵向贯通误差的影响值,σΔYG为横向贯通误差的响值。对于曲线隧道,可以根据线路关系计算出贯通点在控制网坐标系统中的坐标(XG,YG),以及该点的切线方位角(贯通点的纵向方位角)αE和横向方位角αF=αE+90°,因此,隧道横向贯通误差为
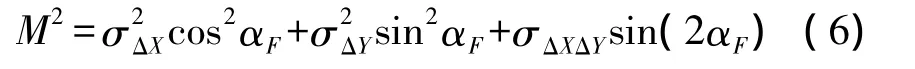
该方法是一种严密的隧道贯通误差预计方法。由于控制网的坐标协因数阵在测量前无法构建获得,因此,该方法适用于控制测量施测后的隧道贯通误差验后预计。
2.近似方法
相关文献报道过一些近似预计方法,主要包括简化公式法、平均相对误差估计法、设计尺寸法等,各方法分述如下。
(1)简化公式法
简化公式的实质是:洞内导线测量误差所引起的隧道横向贯通误差完全由测角误差所引起,测角误差与边长成正比,且与平均边长有关,平均边长越长,则导线测量误差所引起的隧道横向贯通误差越小。洞内导线测角误差引起横向贯通误差可近似表示为
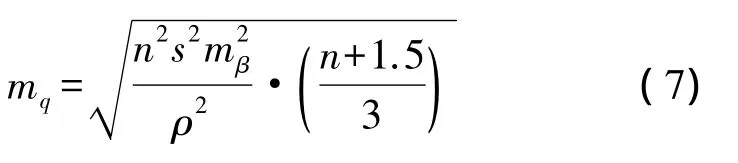
式中,S为导线的平均边长,单位为m;n为导线的边数。
该方法计算更为简便,对于直伸隧道的洞内导线来说,有参考价值。
(2)平均相对误差估计法
按照隧道长度,用GPS控制网平均相对误差1/T估计隧道贯通误差影响值,即

式中,L为隧道长度,单位为m;1/T为GPS控制网平均相对误差。
欧洲隧道公司横穿英法海峡的欧洲隧道采用了该方法。该方法过于简单,没有明确区分横向和纵向贯通误差影响值。所谓控制网平均相对误差,实际上只考虑了边长的相对误差,且控制网的边长非常悬殊。边长的相对误差与边长有关,边长越短,边长的相对误差越大;边长越长,边长的相对误差越小。
(3)设计尺寸法
按照隧道设计尺寸确定横向贯通误差允许值。有文献提出:对于圆形隧道可取设计直径的1/7~1/10作为横向贯通误差的允许值,对于方形隧道可取洞宽1/7~1/10作为横向贯通误差的允许值。这是基于当出现这种横向贯通误差时,完全可以在贯通面附近进行调整,既不会增加开挖量,也不会影响工程的质量和进度来考虑的。该方法很简单,且与隧道的长度无关。
3.本文提出的隧道贯通误差预计方法
(1)坐标差统计法
坐标差统计法原理如下:取隧道轴线为X坐标轴,贯通面与坐标轴垂直,贯通面与Y轴平行。对特长直伸隧道,设只有一个贯通面,且位于中间,按等边设计并模拟从进、出口到贯通面的洞内导线网,如设计成六边形的双导线网。对进、出口洞内导线网分别进行平差,计算出位于贯通面上同一点的X、Y坐标,Y坐标差即为洞内导线测量误差所引起的隧道横向贯通误差。模拟计算几十组(大子样),然后对Y坐标差值作统计计算,即计算Y坐标差的均值、均值的中误差。最后可将均值作为洞内导线网测量误差所引起的横向贯通误差。
该方法的特点是计算严密,使用简便,易于编程实现,子样越大,所得的结果越可靠;而且将进、出口洞内导线网作为一个独立的影响因子一起预计,方法创新,适合各种隧道洞内导线横向和纵向贯通误差影响值计算。
(2)坐标中误差法
坐标差中误差法原理如下:对于特长隧道,按前述坐标系设计进、出口端洞内导线网,分别进行平差,可得到不同隧道长贯通面上点的X、Y坐标及其中误差,可以把X、Y坐标的中误差视为洞内导线测量误差所引起的隧道纵、横向贯通误差,因为进出口端各有一个网,坐标的中误差乘以,即为洞内导线测量误差所引起的隧道横向贯通误差,又因为平差是一次性的结果,在实际作业中,要对洞内导线网作经常性的重复测量,可以乘以一个小于1的系数,如除以,则刚好抵消,因此,可直接把进口端洞内导线网不同隧道长贯通面上点的Y坐标中误差视为洞内导线测量误差所引起的隧道横向贯通误差。
该方法计算非常简单,有理论依据,可直接把进口端洞内导线网不同隧道长贯通面上点的Y坐标中误差视为洞内导线测量误差所引起的隧道横向贯通误差,也适合洞内导线网边加测陀螺方位角后的情况。
(3)微分公式法
微分公式法是在过去的隧道贯通误差严密预计方法即权函数法的基础上,进行改进和扩展,提出的一种适合特长隧道横向贯通误差预计的方法,可扩展到GPS网。其原理如下:设隧道洞外平面控制网及坐标轴、隧道轴线如图1所示,从进口点J和定向点A,经洞内导线推算得贯通点PJ的坐标,从出口点C和定向点B,经洞内导线推算得贯通点PC的坐标,不考虑 βJ、βC、SJP、SCP的误差,隧道洞外平面控制测量误差所引起的横向贯通误差即贯通点PC、PJ的横坐标差 ΔyP的中误差,对 ΔyP进行全微分,可得
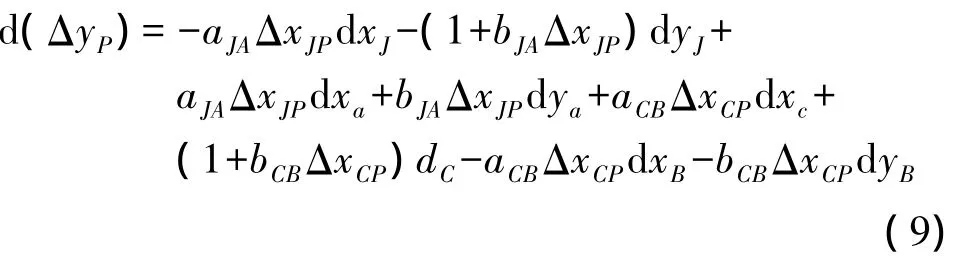
式中,方向系数aJA、bJA可按下式计算
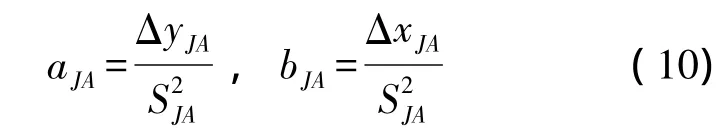
由网的近似坐标不难求得上述全微分式的系数,根据广义误差传播律计算出隧道洞外平面控制测量误差所引起的横向贯通误差。
由上述公式可知,隧道洞外平面控制测量误差所引起的横向贯通误差与隧道两相向开挖洞口的洞口点、定向点的位置及其精度有关,与贯通点的位置有关。对于特长隧道,无论有多少个贯通面,都可按式(9)计算出隧道洞外平面控制测量误差所引起的横向贯通误差。
该方法理论严密,可用于洞外边角网(对于不能布设GPS网时有意义),也可扩展到洞外GPS网。对于GPS网,可以看成是边角全测的全边角网,或边长、方位角全测的网,因此,可用上述全微分式预计GPS网的贯通误差,易于编程实现。
三、隧道横向贯通误差预计实现步骤
1.洞外GPS控制网
隧道洞外横向贯通误差预计采用两种不同的形式,分边角全测和边长方位角全测两种情况,边角全测相当于用全站仪(TPS)测量,边长方位角全测相当于用GPS测量。以某特长隧道(全长20.05 km)实测网为例,该隧道采用“长隧短打”的形式施工,其中左线有7个贯通面,右线有9个贯通面,采用2种模拟法计算出每个短隧道的洞外贯通误差影响值(见表1)。
(1)按GPS网进行估算
1)人工生成隧道洞外GPS网方案文件(* .GFA)。
2)人工生成隧道洞外GPS网贯通误差引导文件(*GPS.GTI)。
3)自动生成洞外GPS网的平差结果文件。
4)估算的贯通误差影响值。
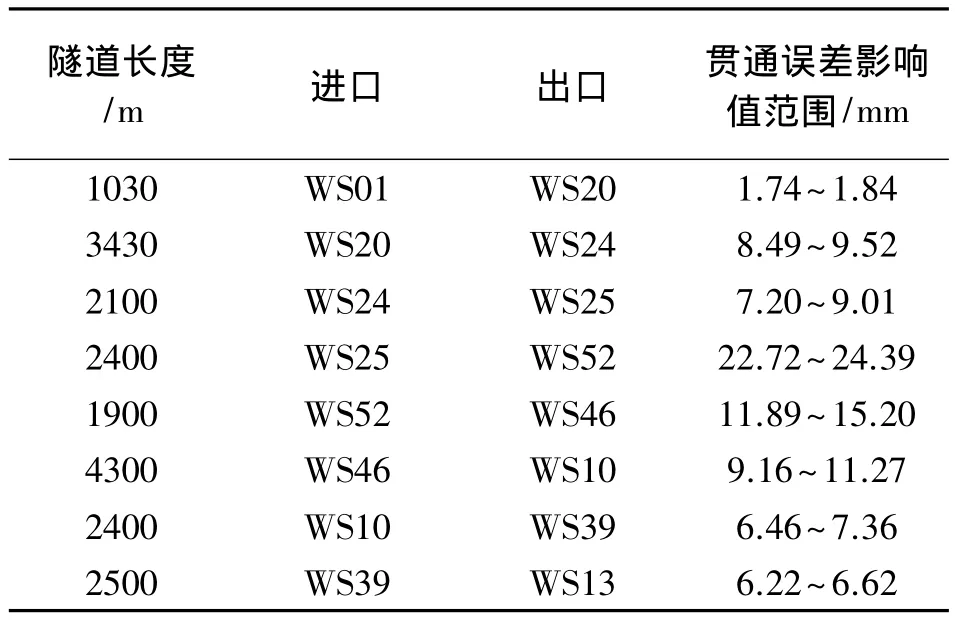
表1 隧道各贯通面的贯通误差影响值(GPS网法)
(2)按边角网进行估算
1)人工生成边角网方案文件(*.FA2)。
2)自动生成边角网观测值文件(*.IN2)。
3)人工生成的隧道洞外GPS网贯通误差引导文件(* .GTI)。
4)自动生成洞外GPS网的平差结果文件平差结果文件。
5)估算的贯通误差影响值(见表2)。
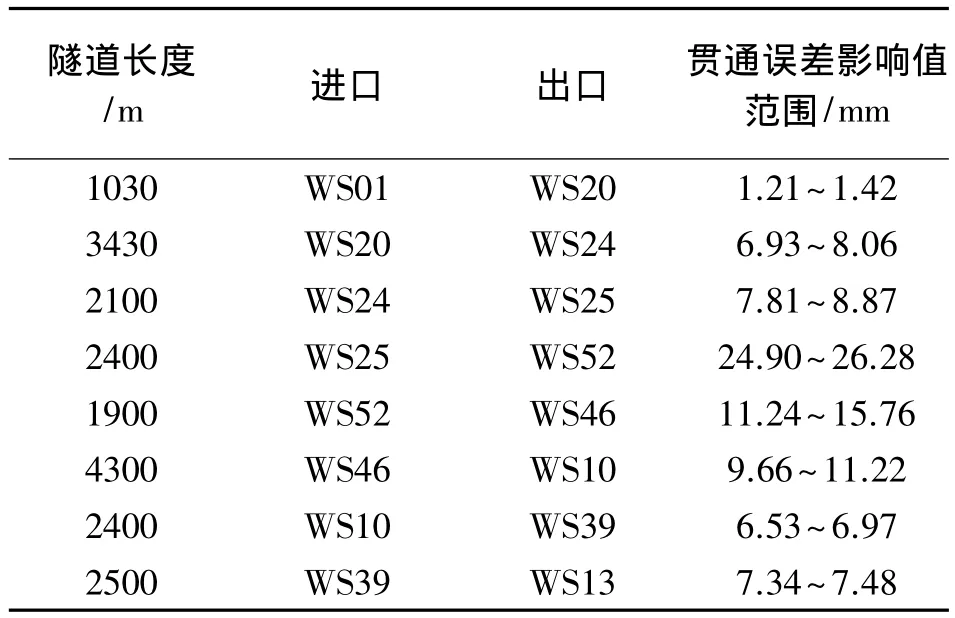
表2 隧道各贯通面贯通误差影响值(TPS网法-全边角网法)
GPS网法和TPS网法-全边角网法两种方法的计算结果基本是一致的,相差都在2 mm以内。
2.洞内导线网
设隧道长50 km,平均边长500 m,按方向中误差为1.0″(测角中误差1.4″)、边长固定误差为2 mm、比例误差为2 mm进行导线网模拟,并对进、出口洞内导线网分别进行平差,计算出位于贯通面上同一点的X、Y坐标。估算步骤如下:
1)人工生成50 km隧道洞内进(或出)口导线网方案文件(*.FA2)。
2)自动生成50 km隧道洞内进(或出)口导线网观测值文件(*.IN2)。
3)平差得50 km隧道洞内进(或出)口导线网平差结果文件(*.OU2)。
4)由平差坐标及其精度可计算进出口洞内导线网在贯通面上点的坐标差,同样可获得洞内导线网点的Y坐标中误差,把其视为洞内导线测量误差所引起的隧道横向贯通误差(见表3)。
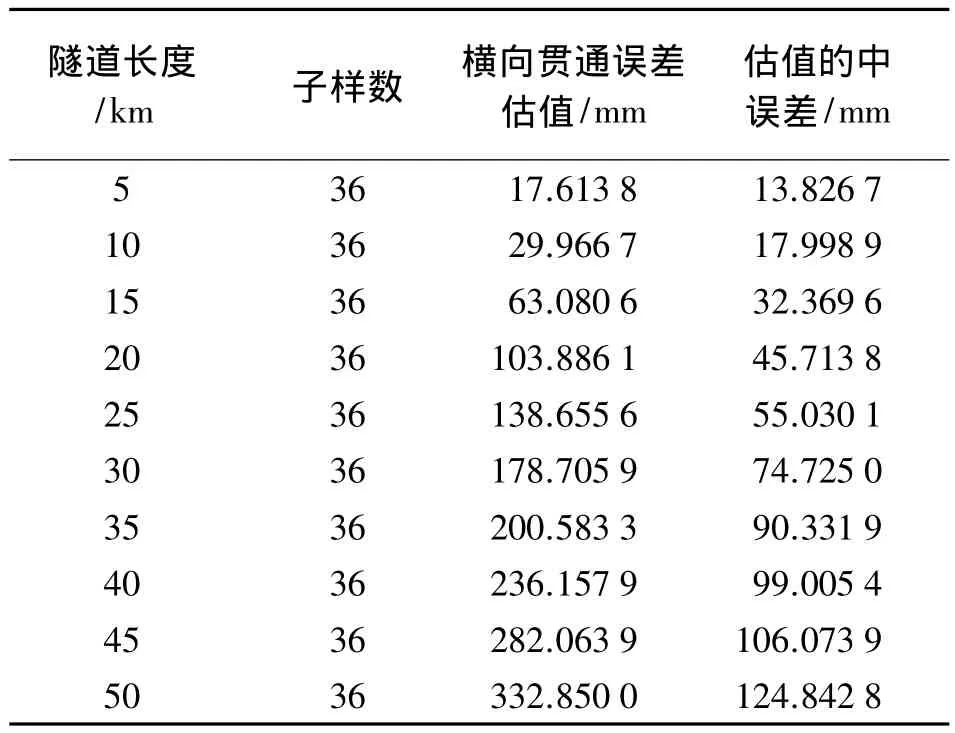
表3 洞内导线网测量误差引起的横向贯通误差估值及中误差 mm
[1]付宏平.乌鞘岭特长隧道控制网布设以及贯通误差预计[J].兰州交通大学学报,2008,27(5):54-57.
[2]张正禄,张松林,伍志刚,等.20~50 km超长隧道(洞)横向贯通误差允许值研究[J].测绘学报,33(1):83-88.
[3]张项铎,张正禄.隧道工程测量[M].北京:测绘出版社,1998:44-66.
[4]TB 10601—2009,高速铁路工程测量规范[S].北京:中国铁道出版社,2010.
[5]张项铎.浅论隧道横向贯通误差估计方法[J].隧道建设,2003(5):5-7,10.
[6]刘成龙,王鹏.基于坐标协因数阵的GPS网隧道横向贯通中误差严密计算方法研究[J].铁道学报,2009(1):74-77.
[7]张怀良.隧道贯通误差预计方法探讨[J].山西建筑,2004(20):230-231.
[8]张项铎.隧道GPS网布测中有关问题的探讨[J].中国铁道科学,2001,22(6):73-78.
[9]孙家兵,薛利华.GPS控制网隧道贯通影响值计算编程实现要点[J].大坝与安全,2004(S0):28-30.
[10]吴连雄,徐一鸣,刘成龙.罗峰隧道施工GPS控制网建网及其贯通误差预计[J].黑龙江工程学院学报,2002,16(4):36-38.
