一种基于最短优先的最短路径算法的实现

萨贤春，辛 赟，陈宪东，杨 超

(1.西安科技大学，陕西 西安710054;2.陕西省测绘地理信息局，陕西西安710054)

一、引 言

路径分析是GIS中网络分析的重要组成部分，其中最短路径算法作为路径分析的主要研究内容，已被应用到诸如机器人运动设计(robot motion planning)、电网、高速公路建设、煤矿风网解算及计算机网络路由等各个方面［1］。现有的最短路径算法按照实现技术可分为标号算法与代数算法两大类。其中标号算法使用比较广泛，其代表的算法有最短优先搜索算法Dijikstra、Floyd等，代数方法有矩阵乘法等［2］。目前所公认的最好的求解最短路径问题的方法是 1959年由 Dijkstra提出的标号法，即Dijikstra算法。本文从蚁群思想出发，通过不同的数据结构与标记方式，设计并实现了一种最短路径求解的新算法。假设从起点开始放出一群蚂蚁，始终是爬行过程中花费最少的一只在向前爬行，通过对每一次爬行过的节点和弧段进行标号的方法来确保该过程是最短优先搜索策略，即搜索到的路径为最短路径。

二、算法描述

广度优先搜索属于一种盲目搜索策略，是最简便的图的搜索算法之一，也是很多重要的图的算法原型。本文所采用的方法就是基于一种广度优先的最短优先搜索思想。

1.算法思想

在一个赋权无向图G(V，E，W)中，已知起始节点s与终止节点d，在起始节点处放置一群蚂蚁(ants)，使得其中始终是爬行过程中花费路径值(mVal)最少的一只蚂蚁在向前爬行(繁殖)，并对每只蚂蚁爬行过的节点与弧段进行标记(isAnt)，若蚂蚁在爬行的过程中遇到已经标记过的节点或弧段，则该蚂蚁停止爬行并死亡(路径死亡)。那么，所有蚂蚁中最先爬到终止节点的，其爬过的路径即为网络G(V，E，W)中起始节点s到终止节点d的最短路径。

2.数据结构

网络中存储的主要要素为网络节点、网络弧段和空间拓扑关系。节点与弧段是基础要素，是组成网络的物理要素，而空间拓扑关系描述的是它们之间的关系。图的拓扑关系存储采用节点与边数据结构，在节点上附加记录与之相连弧段的信息。与邻矩阵的存储方式相比，基于邻近节点的拓扑关系存储方法节省了内存，可用于规模较大的网络分析。本文网络中具体节点结构如下:

3.算法设计运行过程

采用本文所述路径搜索策略的最优路径算法流程如图1所示。图中路径繁殖指的是:对原来的路径向前扩展一个未标记过的弧段，路径值增加该弧段的值。以s与d分别代表起点与终点，算法结束的条件为找到最短路径或图中的节点已经被永久地标记。

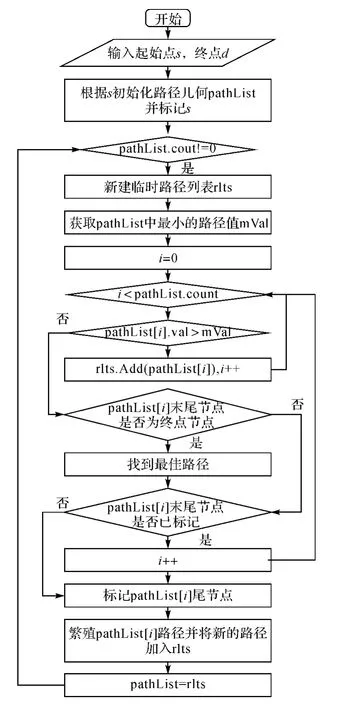
图1 算法流程

以图2为例，使用该算法求解从起点(29)到终点(6)的最短路径。具体执行步骤如下:

1)标记起始节点29，初始化起始路径为29—37、29—27、29—23、29—16，并标记弧段 29—37、29—27、29—23、29—16。

2)因为节点29已被标记过，因此路径29—37、29—27在扩展时死亡。

3)对路径列表中剩余的路径进行扩展。在该网络图中首先繁殖路径29—23。节点23未被标记，因此标记节点 23并扩展，即 29—23—17、29—23—22、29—23—30、29—16;现在最短路径为 29—16，对其进行繁殖，即 29—16—14、29—16—17、29—16—9、29—23—22、29—23—17、29—23—30。其中29—23—22为最短繁殖，但由于23—22已经被标记过，因此该路径死亡。同理由于16—14已被标记，29—16—14 死亡。

扩展当前路径列表中的29—16—9，扩展后为29—16—9—7、29—16—9—10、29—16—9—2、29—16—17、29—23—17、29—23—30。依次类推，按照流程图直到当前的最短路径的末尾节点为终止节点为止。最后的最短路径结果为 29—16—9—10—11—12—13—6，与dijikstra路径算法结果一致。

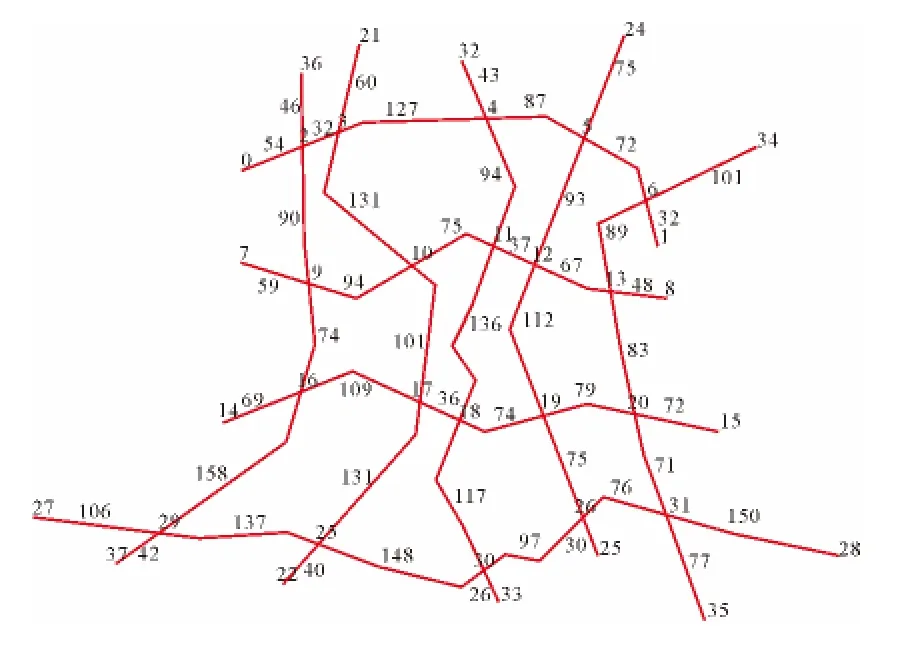
图2

三、算法分析

1.算法证明

定义1:对于有向图G(V，E，W)，Adj(vi)表示节点vi的出度弧段集合，即有向图中以vi为起点的弧段集合。由文献［3］可知，在一般GIS的网络图中，Adj(vi)的个数一般为2～5。

结论1:A为在执行搜索的过程中产生的临时路径集合。存在 ai∈A，mVali为路径集合 A{a1，a2，…，an}中最短路径的路径值。

结论2:对于路径集合A，A中所有的路径均为路径的末尾节点至起始节点的最短路径。

结论3:图G(V，E，W)中从起始节点开始，每次进行路径繁殖的始终是路径集合中值mVal最短且路径的尾节点vi∉P未被标记过，因此最先到达终止节点的路径即为最短路径。

结论2的证明:在搜索过程中对于每一条路径ai，其尾部节点到起始节点的距离di表示路径ai的长度。由于在搜索过程中对扩展过的节点与弧段进行标记，若在搜索过程中某一路径扩展时遇到的节点或弧段已被标记过，则说明至该节点或该弧段有比当前路径更短的路径，因此对该路径扩展一定不能得到最短路径，该路径死亡。根据结论2，一旦搜索至终止节点，则可以确定最短路径，结论3得证。

算法证明过程如下:P={s}，T=V－P，P为标记过的节点集合，T表示未标记过的节点集合。根据起始点s初始化起始路径集合A;标记起始节点s，P={s}，T=V－P。

1)开始进入循环:对于路径集合A{a1，a2，…，an}，若没有从起点s至终点d路径，则根据结论1有

2)对 A{a1，a2，…，an}中每一条路径值 mValk，取长度最短的路径ai为其路径值mVal;其他路径值大于min Val。判断该最短路径的末尾节点vik是否为终止节点d，若是，则找到最短路径，搜索停止，否则进行步骤3)。

3)若路径ai末端的节点vk∈P，则说明至该节点有比路径ai更短的路径，该路径为非最短路径，路径死亡。若vk∈T，则标记vk，使vk∈P。

4)根据结论3，对路径ai进行繁殖，设Adj(vk)中未被标记过的弧段有m个，则原来的ai被繁殖为m条新路径，繁殖后的新路径的路径值mVal增加加入路径弧段的值wkj，使用繁殖后的路径和未进行繁殖的路径更新路径集合A，进入下一次循环，直到找到最短路径或A的个数为0为止。

2.算法效率分析

设k为n次路径集合中路径个数的平均值，k的大小与网络规模的大小有关。从根据起点初始化的路径集合开始，每次对候选路径集合求最短路径采用的是冒泡排序的方式，它的时间复杂度为k2;每次对集合中的最短路径至少向前扩展一个节点，扩展至所有节点n的时间复杂度为nk;每次对最短路径扩展的时候，路径末尾出度节点的个数k1约为2～5，那么对所有节点进行扩展的时间复杂度为nk1。因此，总的复杂度为O(nk2+nk+nk1)。

四、结束语

本文算法从蚁群思想出发，以最短优先搜索为基础，在路径搜索过程中采用对节点与弧段标号的方法确保每次进行繁殖的路径为所有路径中最短的，从而保证搜索过程中从起点开始的路径中首先到达终点的为最短路径。笔者在主频为2.20 GHz、内存为2 GB、操作系统为Windows7的计算机上，使用C#对其运行效率进行了测试，结果见表1。

表1

与传统的方法相比，该算法结构简单，便于理解，执行效率也不逊色，有一定的实用性。同时，本算法也支持并行计算。

［1］严蔚敏，吴伟民.数据结构［M］.2版.北京:清华大学出版社，1997.

［2］陆锋.最短路径算法:分类体系与研究进展［J］.测绘学报，2001，30(3):269-275.

［3］夏松，韩用顺.GIS中最短路径算法的改进实现［J］.测绘通报，2004(9):40-42.

［4］王明中，谢剑英，陈应麟.一种新的Kth最短路径搜索算法［J］.计算机工程与应用，2004(30):49-89.

［5］司连法，王文静.快速Dijkstra最短路径优化算法的实现［J］.测绘通报，2005(8):15-18.

［6］陈洁，陆锋.交通网络最短路径标号算法的实现与效率分析［J］.中国图象图形学报，2005，10(9):1134-1138.

［7］王臣杰，毛海城，杨得志.图的节点-弧段联合结构表示法及其在GIS最优路径选取中的应用［J］.测绘学报，2000，29(1):47-51.

［8］YUE Y.An Efficient Implementation of Shortest Path Algorithm Based on Dijkstra Algorithm［J］.Journal of Wuhan Technical University of Surveying and Mapping，1999，24(3):209-212.

［9］高松，陆锋，段滢滢.一种基于双向搜索的K则最优路径算法［J］.武汉大学学报:信息科学版，2008，33(4):418-421.

［10］徐业昌，李树祥，朱建民.基于地理信息系统的最短路径搜索算法［J］.中国图象图形学报，1998，3(1):39-42.