B样条曲线全局插值优化算法及其实现

B样条曲线全局插值优化算法及其实现

吴婷1,2，邹海2

(1.安徽国防科技职业学院 网络信息中心， 安徽 六安 237011；

2.安徽大学 计算机科学与技术学院， 安徽 合肥 230601)

[摘要]通过插值给定的数据点来创建B样条曲线时，需要对曲线的初始形状进行多次修改。为使首次生成的曲线更接近设计者的意图，从数据点参数化和确定节点矢量两个方面优化了现有算法。提出了一种改进的弦长参数化方法来求取给定数据点的对应参数值，改善了数据点急转弯处的过渡情况；通过平均值法确定节点矢量，有效避免了系数矩阵中奇异方程组的产生。总体上实现了一种B样条曲线全局插值的优化算法，最后对两组典型数据点的实验直观地验证了该算法的可行性。

[关键词]B样条曲线；全局插值；优化算法

[文章编号]1673-2944(2015)03-0071-04

[中图分类号]O241.5

收稿日期：2014-11-13

基金项目：国家科技重大专项基金资助项目(2009ZX05039-004)

作者简介：吴婷(1983—)，女，安徽省金寨县人，安徽国防科技职业学院实验师，安徽大学硕士研究生，主要研究方向为计算机应用技术；邹海(1969—)，男，安徽省寿县人，安徽大学副教授，硕士生导师，博士，主要研究方向为智能计算、中间件技术。

B样条在CAD领域受到人们的广泛关注，非均匀有理B样条由于诸多优点而被确定为工业产品物理形状的唯一数学方法[1-2]。在参数化设计B样条时，由于通过控制顶点来直接生成曲线的方法很难得到满意的形状，设计者一般先通过给定一系列关键点来确定曲线的大致形状，再由造型系统反算出控制顶点进而插值这些关键点，生成初始的B样条曲线[3-4]。由于曲线插值的结果存在不唯一性，初始曲线可能与设计者意图之间存在较大的出入，通常需通过调整控制顶点或调节权重系数反复修改曲线形状，才能最终获得满意的设计结果[5-6]。设计者的思想正是通过给定数据点的分布情况来表达的。因此，为了提高设计效率，应该使初次生成的曲线尽可能合理地反映数据点分布。B样条曲线插值最重要的任务就是确定节点矢量和各给定数据点对应的参数值，合理的参数值和节点矢量有利于更快地获得理想的设计效果，提高设计效率。

确定给定数据点所对应参数值的方法不一，目前常用的有均匀参数化和弦长参数化，而节点矢量则常用等距分布法[5]。当数据点分布不均匀时，采用均匀参数化会出现打圈相交的现象，容易产生与原始设计意图较大的偏差，不利于分析和控制曲线形状。而对于弦长参数化，则当给定数据点急转弯变化时会出现过大的曲率变化，亦难以获得满意的效果。采用等距分布确定节点矢量的方法容易产生奇异方程组，给系数矩阵的求解增加了难度。在对给定数据点进行插值拟合的研究中，Gofuku等[7]提出了满足多个数据点处切向量的算法，但这些算法主要用于数据点分布较均匀的场合，否则插值的效果不够理想。为此，本文充分考虑相邻两个给定数据点之间的距离对曲线形状的影响，拟采用改进弦长参数化方法，结合平均值法确定节点矢量，力图使曲线走势更准确地反映出给定数据点分布情况。

1　 B样条曲线的定义

一条p次B样条曲线定义为[6]：

(1)

其中：a≤u≤b；Pi是曲线的控制顶点；Ni,p(u)是p次B样条基函数；定义域为非周期节点矢量U，其数值在区间[ui,ui+p+1)上非零，并按照公式(2)和(3)求取：

(2)

(3)

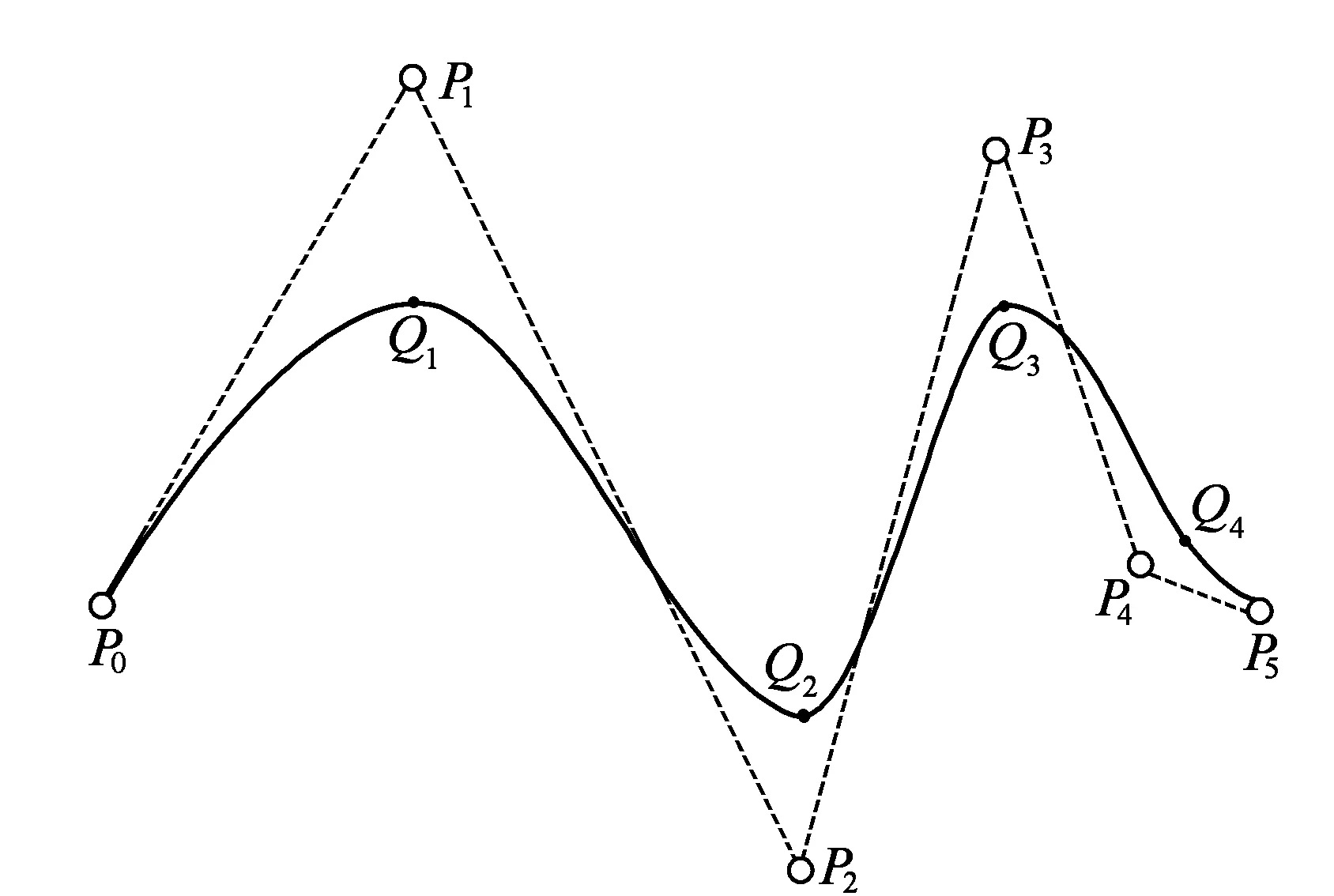
图1　B样条曲线控制多边形示意图

节点矢量U中a和b的重复度都为p+1，除非特别声明，通常取a=0，b=1。如图1所示，依次连接控制顶点即为控制多边形。

2　给定数据点的 B样条曲线插值算法

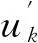
(4)

其中：k=0,1,…,n；n+1个控制点Pi是待求的未知量。

2.1求取参数值

为使最终获得的曲线能充分反映出给定型值点的分布情况，兼顾曲线的光滑性，此处采用改进的弦长参数化，即对弦长进行开3次方运算，旨在适当降低弦长的直接影响，改善曲线在数据点处的过渡平滑性。

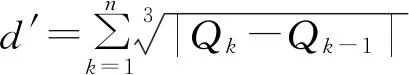
(5)

2.2　确定节点矢量

从理论上讲，节点矢量可以等距分布，即u0=…=up=0，um-p=…=um=1，uj+p=1/(n-p+1)，j=1,2,…,n-p。但是如果将其与公式(5)联合使用，方程组(4)可能变成奇异方程组。为避免这种情况出现，此处采用取平均值的方法，中间的节点矢量用公式(6)求出：

(6)

2.3反算控制顶点

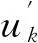
(7)

3　算法应用实例

为直观地比较所提算法与均匀参数化和弦长参数化方法的不同效果，以两组较典型的数据点为例，分别用上述3种方法进行2次和3次非有理B样条插值，其结果如图2所示。

第一组数据点为Q=[8，9；12，12；16，10；22，15；30，11；36，13；45，9]，所得对应的参数为Uk=[0，0.11，0.28，0.50，0.65，0.88，1.0]，节点矢量为U=[0，0，0，0.19，0.39，0.57，0.76，1.0，1.0，1.0]，全局插值所得的2次B样条曲线见图2(a)。

第二组数据点为Q=[-2，-4；10，0；6，20；21，40；36，20；32，0；44，-4]，所得对应的参数为Uk=[0，0.17，0.39，0.60，0.78，0.89，1.0]，节点矢量为U=[0，0，0，0，0.39，0.59，0.75，1.0，1.0，1.0，1.0]，全局插值所得的3次B样条曲线见图2(b)。

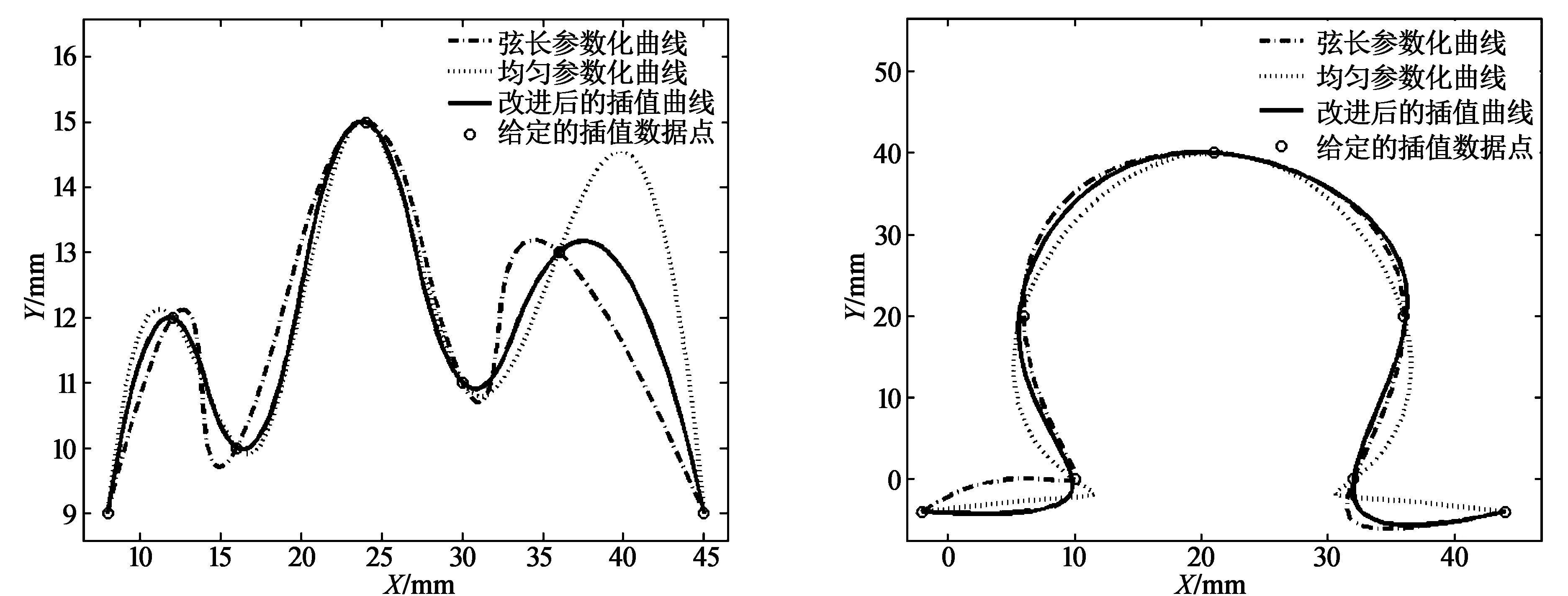
(a) 全局插值所得的2次B样条曲线　　　　　　　　　　(b) 全局插值所得的3次B样条曲线

由图2可见，采用改进后的参数化方法所得到的插值曲线，可以更好地处理各数据点处的过渡，没有出现曲率突变的情况，使曲线更光滑，更合理地反映了数据点的分布情况。

4　结　论

对于给定数据点的非有理B样条曲线插值，两个重要环节就是数据点参数化和节点矢量的确定，它们将影响曲线的形状。本文在分析现有算法的基础上，提出了一种改进的参数化和确定节点矢量的方法，结合反算出的控制顶点，总体上实现了一套曲线插值方法，该方法可以较准确地反映出设计者的意图，若在此基础上形状修改，则易于构造所需的NURBS曲线。最后对两组数据点进行的仿真实验，验证了该算法的可行性和有效性。

[参考文献]

[1]于谦,李缨,张彩明.基于切向约束构造复合二次B样条插值曲线[J].计算机学报,2014,37(6):1342-1351.

[2]WEN Wei-bin,JIAN Kai-lin,LUO Shao-ming.2D numerical manifold method based on quartic uniform B-spline interpolation and its application in thin plate bending[J].Appl.Math.Mech.Engl.Ed.,2013,34(8):1017-1030

[3]叶铁丽,李学艺,曾庆良.基于误差控制的自适应3次B样条曲线插值[J].计算机工程与应用,2013,49(1):199-216.

[4]刘晶,施侃乐,雍俊海,等.利用控制顶点插值的光滑B样条曲线构造方法[J].计算机辅助设计与图形学学报,2011,23(5):813-819.

[5]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.

[6]LES P,WAYNE T.非均匀有理B样条[M].2版.赵罡,穆国旺,王拉柱,译.北京:清华大学出版社,2010.

[7]GOFUKU S,TAMURA S,MAEKAWA T.Point-tangent point-normal B-spline curve interpolation by geometric algorithms[J].Computer Aided Design,2009,41(6):412-422.

[责任编辑：魏 强]

Optimization algorithm of B-spline curve global interpolation

and its implementation

WU Ting1,2,ZOU Hai2

(1.Network Information Center, Anhui Vocational College of Defense Technology, Lu’an 237011, China;

2.School of Computer Science and Technology, Anhui University, Hefei 230601, China)

Abstract:In the course of creating a B-spline curve by interpolating the given data points, it is needed to modify the initial shape of the curve repeatedly. In order to make the initial curve closer to the designers’ intentions, the existing algorithms were improved from two aspects of the data point parameterization and node vector determination. A modified method of chord length parameterization was put forward to calculate corresponding parameters for data points, and it could improve the transition of sharp turning. A method of average value was presented to obtain node vector, and it could effectively avoid the singular equations in coefficient matrix. On the whole, an algorithm of B-spline curve global interpolation was optimized, and in the end, the feasibility of the algorithm was visually proved by the experiment with two groups of typical data points.

Key words:B-spline curve;global interpolation;optimization algorithm