基于改进和声算法的有序样本聚类及其应用

基于改进和声算法的有序样本聚类及其应用

李晓康

(陕西理工学院 数学与计算机科学学院， 陕西 汉中 723000)

[摘要]标准和声算法只能解决连续型优化问题，而有序样本聚类属于离散型优化问题。将Fisher算法和和声算法相结合，提出一种改进和声算法，使之能够用于离散型优化问题，并利用其对有序样本进行分类。数值仿真实验结果表明，该算法分类结果符合实际。结论表明改进和声算法是一种全局最优算法，分类结果优于Fisher算法。

[关键词]和声算法；有序样本；自相关系数；离差平方和；聚类

[文章编号]1673-2944(2015)03-0065-06

[中图分类号]TP301.6

收稿日期：2014-12-31

基金项目：陕西省教育厅科学研究计划项目(2013JK0616)；陕西理工学院科研基金资助项目(SLGKY14-19)

作者简介：李晓康(1973—)，男，陕西省汉中市人，陕西理工学院讲师，硕士，主要研究方向为应用概率统计。

聚类分析是研究分类的数理统计方法。聚类的关键是定义一个合适的距离，不同的距离定义会产生不同的聚类结果，常用的有最短距离法、最长距离法、重心法、类平均法、离差平方和法等[1]。聚类方法已广泛应用于金融、经济领域，取得了较好的结果[2-4]。

有序样本是指按照时间或其它指标排列的一组样本，在分类过程中不允许打乱原有的样本顺序，只能将相邻的样本聚为一类。有序样本聚类问题求解采用的算法主要有：系统聚类法、传统的Fisher算法、遗传算法等。

和声搜索(Harmony Search，HS)算法[5]是一种新的启发式优化算法，通过模拟音乐家创作音乐和调节和声的过程反复调整和声记忆库中的解，从而完成优化过程。HS全局搜索能力强，并且结构简单，很容易在各种软件和硬件中实现，引起很多科学研究者和工程设计人员的关注，近年来，已经广泛应用于实践优化问题中[6-9]。

本文在Fisher算法的基础上，引进样本一阶自相关系数为分类指标，将有序样本聚类问题转化为一个离散型优化问题，对标准和声算法进行改进，利用和声搜索算法的全局最优求解能力，在不打乱原有样本顺序的条件下，对有序样本进行分类，并确定最终分类数及分类结果。所得结果不同于Fisher算法的近似解，为全局最优解。

1　Fisher算法与和声算法

1.1　Fisher算法

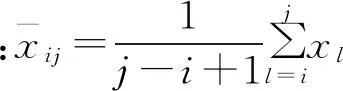
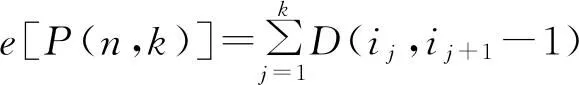
Fisher算法的思想为二分法，即首先将所有样本分为两类，再将其中一类(包含2个以上样本)分为两类，如此递推。故其给出的是局部最优解。

1.2　自相关系数

传统聚类的指标是样本间的距离，常用的有绝对值距离、欧氏距离、马氏距离等。有序样本的聚类是按相邻样本间的相依关系，在不打乱原有样本次序的前提下，将相依关系最强的相邻样本聚为一类，依次进行，直到所有样本聚为一类。但是，传统的距离并不能够真实反映样本间的相依关系强弱，如有4个有序样本，其样本观测值分别为1、2、101、102，若按照绝对值距离，则1、2号样本的距离为1、3、4号样本的距离也为1，显然，3、4号样本的相依关系要强于1、2号样本。可见，传统的距离并不能真实反映样本间的相依关系。受物理中相对误差概念的启发，可考虑定义描述相邻样本间相依关系的相对指标。

一阶自相关系数反映前后样本相依关系程度，即：

(1)

1.3　标准和声算法

标准和声算法的基本思想：(1)产生随机和声记忆库；(2)利用和声调节规则产生新和声；(3)更新操作，即新和声优于和声记忆库中最差和声时，用新和声进行替换，否则重新产生新和声，直至满足终止条件。

标准的和声搜索算法主要用于求解实数优化问题，而有序样本聚类问题是离散组合优化问题，还要求解元素具有有序性。

2　改进和声算法

对于有序样本的聚类问题，可以转换为一个全局优化问题，模型如下：

(2)

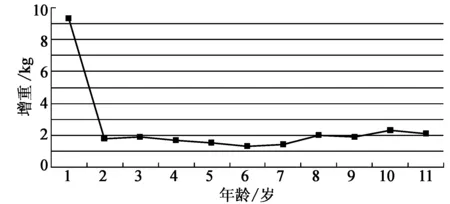
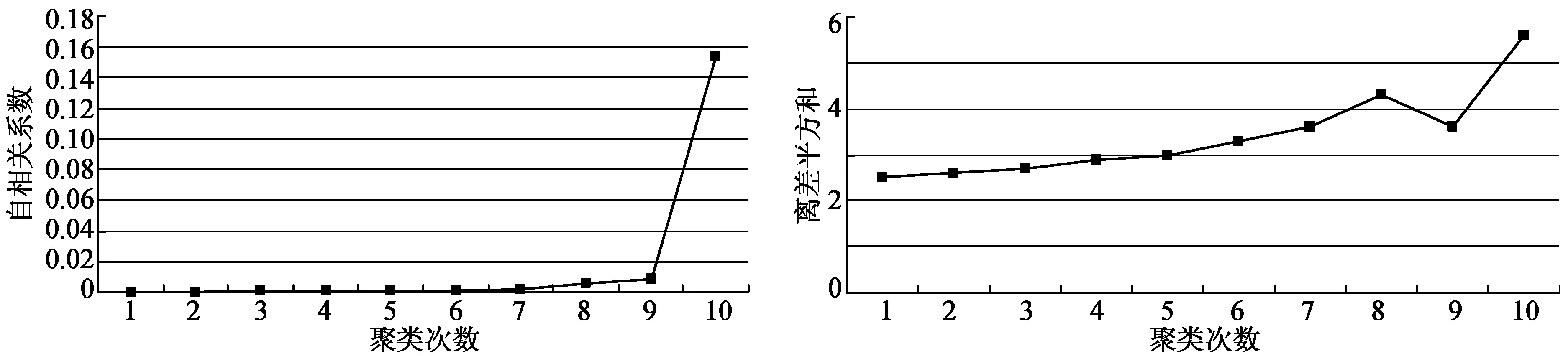
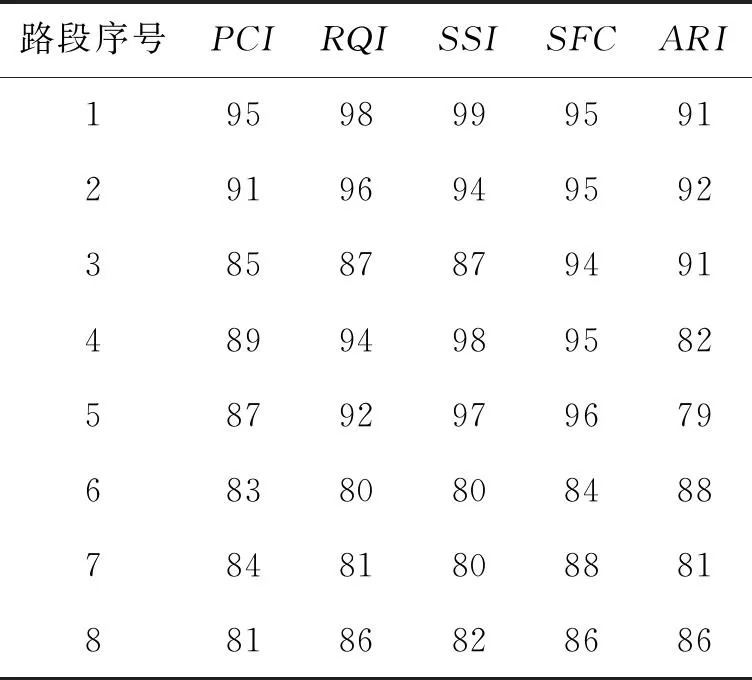
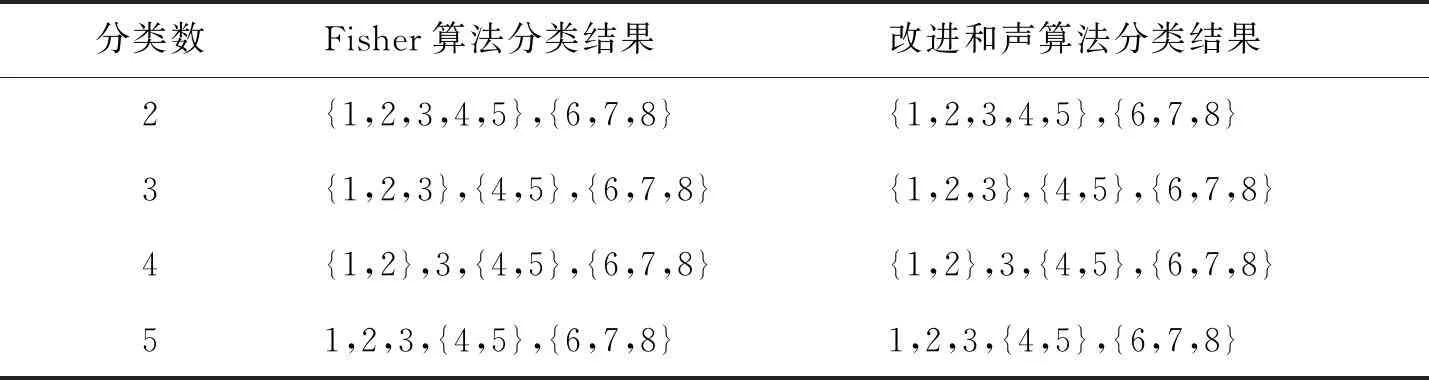
该模型要求找到一个最佳的k值及一个有序样本分割点(j0，j1，j2，…，jk)，其中，j0=1，jk=L(L是样本个数)，且j0

该问题是一个组合优化问题，但不同于传统组合优化问题的是该问题要求分割点必须有序。因此，本文提出一种解决有序样本聚类问题的改进和声搜索算法，算法流程如图1所示。

图1　改进和声搜索算法流程图

在流程图1中，Hnew表示新产生的和声，HM(a，i)表示从HM中随机选取的第a个和声的第i维。HM(idxworst，：)表示和声记忆库(HM)中最差和声向量，idxworst是最差和声在和声记忆库HM中的索引。

本文算法具体步骤如下：

(1)初始化算法参数，设置HMS=15，HMCR=0.98，PAR=0.3；

(2)和声记忆库初始化，参与随机算法进行初始化，为了保证分割点有序，将其从小到大进行排序；

(3)根据适应值函数(2)式计算个体的适应值；

(4)产生一个新个体；

(5)判断是否满足终止条件，如果是，输出最优结果，否则，转至(4)继续。

实现该算法的源程序代码如下：

Hnew(0)=1；

Hnew(k)=n；

For i=1 to k-1

If Rand

Hnew(i)=HM(a，i)，a∈{1，2，…，HMS}

If Rand

Hnew(i)=Round(HM(a，i)+(rand-1)*2)；//在当前点左右进行微调

EndIf

Else

Hnew(i)=Rand(Hnew(i-1)，n)；//在Hnew(i-1)和n之间随机产生一个点

EndIf

EndFor

Hnew=sort(Hnew)；//进行排序修正，使得分割点有序

If Hnew<=HM(idxworst，：)

HM(idxworst，：)=Hnew；

End

不同于Fisher算法的是，改进HS算法是基于目标函数进行全局优化，并不依赖于前面的分解结果。由此可见，改进和声搜索算法通过对所有样本点进行综合判断，进行全局搜索，故能够获得全局最优解。

3　算例分析

以下给出两个基于和声算法的有序样本聚类的算例。

3.1　一维有序样本聚类

为研究儿童的生长规律，统计男孩从出生至11岁每年平均增加的体重，数据见表1。分析表中数据，希望从中找出儿童体重变化规律，将相邻的某些年龄段分为一个阶段，得出儿童体重变化各阶段特征。为此，利用有序样本聚类方法对其分类。

表1　各不同年龄段儿童体重增重数据

首先，做出其数据散点图如图2所示。可以看出：儿童在不同年龄阶段的增重具有明显变化，故可根据在不同年龄段的增重特征将其分为几个阶段。所以可采用有序样本的分类方法处理。

图2　年龄与体重增重关系图

按照(1)式定义，对所给数据，计算其一阶自相关系数，结果如表2所示。采用(1)式定义相邻样本间的距离，利用Fisher算法和本文提出算法，对本例样本的聚类过程如表3所示。

表2　相邻样本一阶自相关系数

表3　两种算法的分类结果

注：括号内数字为每一类包含的样本序号，如：k=3时，分为3类：{1}、{2，3，4，5，6}、{7，8，9，10，11}。

改进和声算法各次分类的聚类距离(自相关系数)和离差平方和e[P(11，k)](k=1，2，…，10)如表4所示，图形如图3、图4。

表4　改进和声算法各次聚类距离(自相关系数)和离差平方和

图3　各次聚类的自相关系数　　　　　　　图4　各次聚类的离差平方和

比较两种分类方法的过程和结果可以看出：(1)改进和声算法的分类过程是“分”，即每次将有序样本在某点“断开”，而Fisher算法的分类过程是“合”，即每次将距离最近的相邻样本“聚拢”；(2)Fisher算法的后一次聚类是在前一次的基础上，而改进和声算法的后一次“分”与前一次结果无关，是在全局范围内重新搜索，故给出的是全局最优解。

最佳分类数的确定一方面依赖于专业知识，根据儿童生长发育规律及特点，可分为以下几个阶段：出生后的迅速生长阶段0~2岁，平稳生长阶段3~7岁，二次发育阶段8~11岁；另一方面，可结合分类过程的自相关系数及离差平方和的变化规律确定分类数。综合以上两方面，由图3和图4可以看出，经过7次分类(类的个数为4)，类间的自相关系数和离差平方和均有比较明显的增加，故确定的最优分类数为4，最终分类结果为：1，{2，3，4}，{5，6，7}，{8，9，10，11}。分类结果符合儿童生长发育特点和规律，分类结果合理。

3.2　多维有序样本聚类

表5　某路段路面性能检测数据

公路养护单元xi(i=1，2，…，n)是一多维向量，每一维代表该单元的一个属性。现考虑5种路面属性：路面结构性能(PCI)、路面功能性能(RQI)、结构承载能力(SSI)、路面安全性能(SFC)、抗车辙指数(ARI)。每一养护单元可用1×5向量xi=(xi1，…，xi5)(i=1，2，…，n)表示，其中xij(j=1，2，…，5)表示第i路段的第j项指标值。其原始数据如表5[10]所示。

此问题的8个路段为连续有序路段，相邻路段具有一定程度的相似性，在分类时，不允许打乱原有顺序，只能将相邻路段分为一类。对其按照如上介绍的和声算法进行有序样本聚类，聚类结果如表6所示。

对于本例，两种分类结果一致。在实际应用中，结合公路路面养护要求，通常将路段分为3个类型，结合本文算法结果，最终分类如下。第一类：{1，2，3}，此类为路面性能较好路段，各路面性能指标较好；第二类：{4，5}，此类为路面性能中等路段，各路面性能指标中等；第三类：{6，7，8}，此类为路面性能较差路段，各路面性能指标较差。

表6　两种算法的分类结果

4　结　论

将有序样本的Fisher算法与传统的系统聚类法相结合，引入样本一阶自相关系数描述相邻样本的相依关系，相对传统样本间的距离，能够更好地描述相邻样本间的相依关系，以此作为分类指标，利用和声算法的全局最优搜索能力求解分类过程，所得结果与传统Fisher算法相比，为全局最优解。运用各次分类的离差平方和确定最终分类数及分类结果，能够得到更加合理的分类结果。

[参考文献]

[1]张尧庭，方开泰.多元统计分析引论[M].北京：科学出版社，1999：444-452.

[2]严广松，路允芳.多维有序样本的聚类方法研究[J].统计与决策，2008(4)：29-30.

[3]毛定祥.基于因子分析与有序样本最优分割的商业银行盈利性流动性安全性综合评价[J].上海大学学报：自然科学版，2007，13(1)：105-110.

[4]苏庆利.有序样本聚类法在经济分析中的应用[J].统计研究，2006(7)：76-77.

[5]PAN Q K，SUGANTHAN P N，LIANG J J，et al.A local-best harmony search algorithm with dynamic subpopulations[J].Engineering Optimization，2010，42(2)：101-117.

[6]PAN Q K，SUGANTHAN P N，TASGETIREN M F，et al.A self-adaptive global best harmony search algorithm for continuous optimization problems[J].Applied Mathematics and Computation，2010，216(3)：830-848.

[7]PARIKSHIT Y，RAJESH K，PANDA S K，et al.An Intelligent Tuned Harmony Search algorithm for optimization[J].Information Sciences，2012，196(1)：47-72.

[8]DAS S，MUKHOPADHYAY A，ROY A，et al.Exploratory Power of the Harmony Search Algorithm：Analysis and Improvements for Global Numerical Optimization[J].Systems，Man，and Cybernetics，Part B：Cybernetics，2011，41(1)：89-106.

[9]TUO Shou-heng，YONG Long-quan.An improved harmony search algorithm with chaos[J].Journal of Computational Information Systems，2012，8(10)：4269-4276.

[10]王佳，胡列格.养护路段的有序聚类划分[J].系统工程，2008，26(11)：71-74.

[责任编辑：谢 平]

Cluster of ordered sample and its application based on harmony search algorithm

LI Xiao-kang

(School of Mathematics and Computer Science， Shaanxi University of Technology，

Hanzhong 723000， China)

Abstract:The standard harmony search algorithm can only solve continuous optimization problems，whereas the ordered sample cluster belongs to discrete optimization problems. Combining the Fisher algorithm and the harmony search algorithm，an improved harmony search algorithm is proposed to be used for discrete optimization problems，and for classifying ordered sample. The experimental results show that classification result is consistent with the actual. The conclusion shows that the improved harmony search algorithm is a global optimal algorithm and its result is better than the Fisher algorithm.

Key words:harmony search algorithm；ordered sample；self-correlation coefficient；square deviation；cluster