穿甲弹对均质装甲板毁伤效能的数学研究*

李建平，程 军，熊 伟，郭晓刚

(63863部队，吉林白城 137000)

0 引言

穿甲弹是依靠动能以碰击方式来毁伤目标的弹药，常用来毁伤装甲目标，广泛配用于各种火炮。常用的有用来毁伤飞机、导弹的高炮穿甲弹，毁伤舰船的穿甲弹及半穿甲弹，毁伤坦克、装甲车等目标的脱壳穿甲弹，如图1～图3所示。

穿甲弹穿甲威力是指在规定射程内弹丸从正面击穿装甲目标的能力，常用穿甲体(穿甲弹参与穿甲的部分)的下述指标描述［1］。

1)对靶板的穿透率:对一定的装甲目标，每种弹丸都有各自50%穿透率的速度(V50)，其标准方差记为σV50。穿甲弹的V50越小表示其穿甲效能越好，σV50越小表示其穿甲效能的稳定性越好。目前我国对穿甲弹威力的评价指标使用90%穿透率的速度V90，V90与V50的关系为:

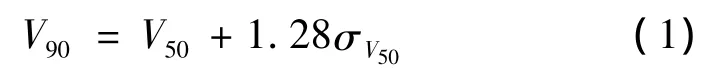
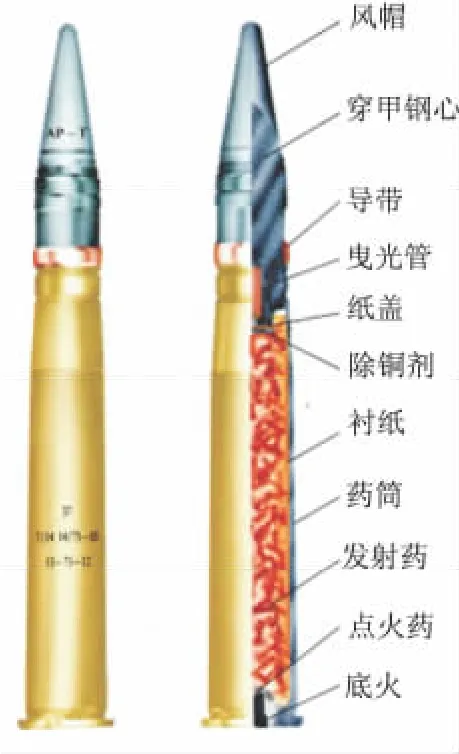
图1 高炮曳光穿甲弹

2)极限穿透速度(Vc):对一定的装甲目标，每种弹丸穿透目标的最小速度。当装甲目标性能相同时，弹丸的Vc越小其穿甲效能越好，一般Vc可认为与V90近似相等。

上述评价方式只考虑了弹目系统中二者位置固定不变的一种特殊工况，不能全面描述穿甲体的毁伤效能。下面提出一种新的穿甲弹毁伤效能描述方法。

图2 被帽穿甲弹

图3 脱壳穿甲弹

1 易损性

目标易损性是指在战斗状态下目标被发现并受到攻击的难易程度，包括战术易损性和结构易损性。战术易损性是指目标被探测装置探测到、被威胁物体命中的可能性，也称目标敏感性。结构易损性是指目标在被探测到的条件下，在弹药的毁伤元素作用下被毁伤的可能性［2］。

1.1 目标结构易损性

结构易损性从狭义角度讲可理解为毁伤元对目标的机械硬杀伤，从广义角度讲应与目标作战效能的下降有关，可用下面几个定义［3］来描述。

1)目标效能:目标系统在规定的条件下，完成其规定任务的能力，用E表示。

2)毁伤元素:能对目标系统效能产生负影响的各种物理因素，用毁伤元素向量 X=［x1，x2，…，xn］T表示。

3)目标结构易损性:目标系统效能在各类毁伤元素的作用下释放的速度，用V表示，可将目标结构易损性表示成如下形式:

4)目标毁伤程度:经历某一毁伤过程，目标系统效能的变化量。

1.2 目标结构易损性的数学描述

为了研究方便作如下假设:

1)目标效能由 a1，a2，…，ak项基本能力构成，效能E可表示为:

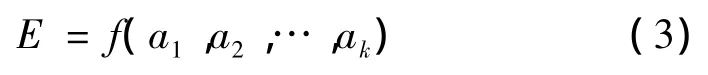
2)毁伤元素有n种，毁伤元素向量可表示成X=［x1，x2，…，xn］T，由式(2)、式(3)可建立目标结构易损性的解析式:

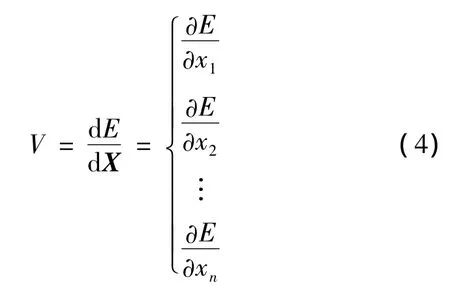
由复合函数的求导法则可得:

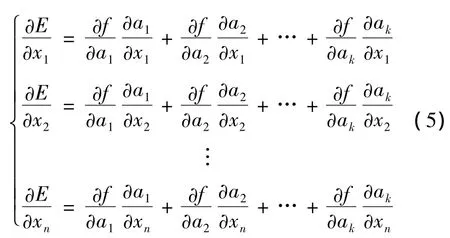
1.3 装甲板对穿甲体易损性的数学描述

1)装甲板防护效能的物理量及数量化

装甲板的防护效能是指其阻止穿甲体穿透的能力，这种能力可用穿甲体的侵彻深度与装甲板厚度的关系来描述，其表达式为:

由式(6)可知，装甲板防护效能值随穿甲体侵彻深度h(0～H)的变化在区间(1～0)内变化。当侵彻深度由hj→hk(0≤hj＜hk≤H)时，装甲板防护效能值的变化量称为防护效能释放量(毁伤程度)，其表达式为:

2)穿甲体穿甲效能的物理量及数量化

穿甲体主要依靠动能对目标进行毁伤，穿甲体确定后其动能只与着靶速度相关，可用着靶速度v与极限穿透速度Vc的比值来描述穿甲体的穿甲效能:

当着靶速度由vj→vk(0≤vj＜vk≤Vc)时，穿甲体穿甲效能值在区间(0～1)内变化。其表达式为:

将式(7)、式(9)代入式(5)可得装甲板对穿甲体易损性的数学表达式:

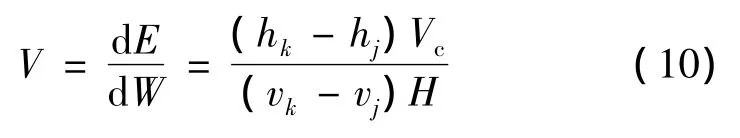
2 装甲板易损性、毁伤程度的计算

装甲板的易损性及毁伤程度是对于特定弹靶［4］系统而言的。以结构如图4所示的钨实心穿甲体(参数见表1)和尺寸为1 m×1 m×0.1 m的装甲板组成的弹目系统(如图5所示)为例，进行靶板易损性和毁伤程度的计算。

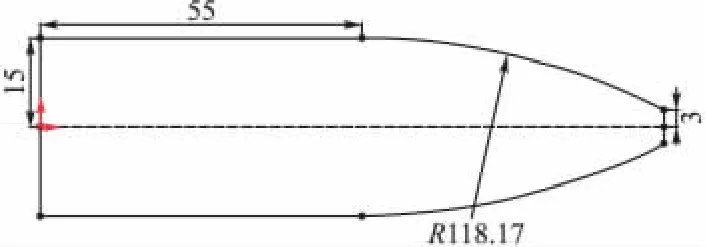
图4 30 mm穿甲体结构示意图

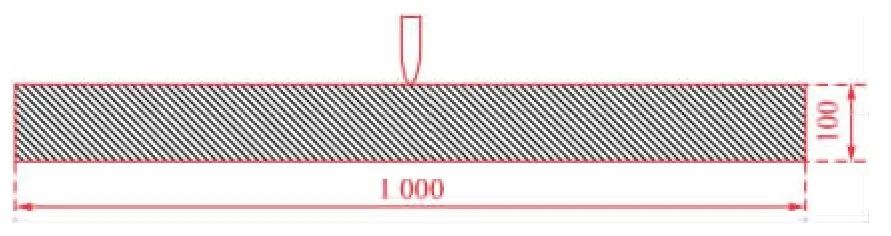
图5 弹靶系统示意图

表1 弹丸结构参数

2.1 侵彻深度计算

德玛尔公式适用于靶板材料均匀、弹丸只做直线运动、弹丸在碰撞靶板时不变形、靶板无位移、弹丸所有动能都用于击穿靶板的弹靶系统［5］，其表达式为:

式中:Vc为极限穿透速度(m/s);d为弹丸直径(dm);h0为靶板厚度(dm);q为弹丸质量(kg);K:穿甲系数(一般取2 400)。

用式(11)、式(7)、式(9)、式(10)计算图 5所示工况，在不同着靶速度条件下，穿甲体穿甲效能变化量、装甲板防护效能释放量、装甲板对穿甲体的易损性。计算过程中 hj=0、vj=0、Vc=955.82、H=1.0。计算结果见表2。

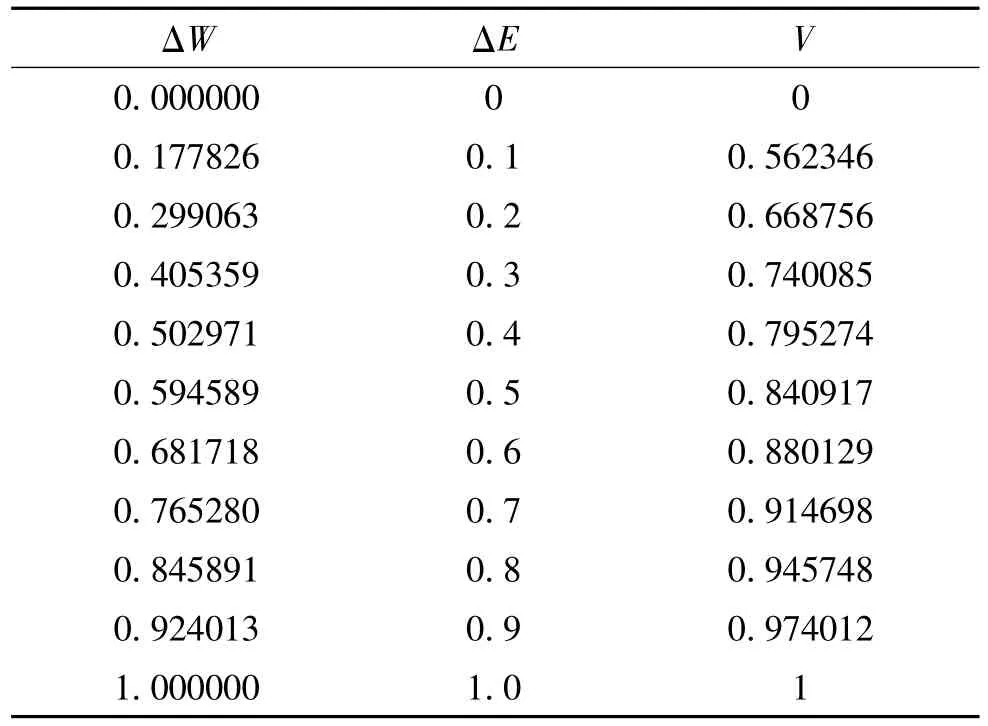
表2 易损性计算结果

2.2 数据拟合

以表2中数据ΔW、V为横纵坐标，选用非线性拟合工具中的Allometric函数进行拟合，拟合曲线如图6所示，结果见表3。同上以ΔW、ΔE为横纵坐标作拟合曲线所示，结果见表4。

表3 ΔW-V拟合结果

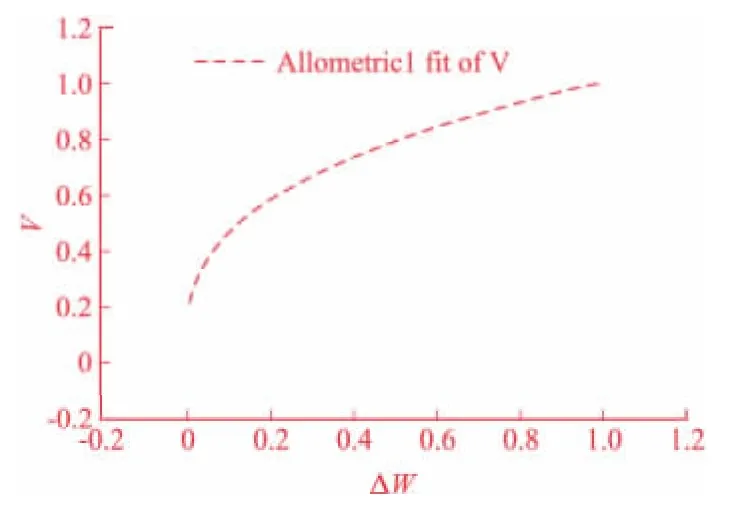
图6 ΔW-V拟合曲线

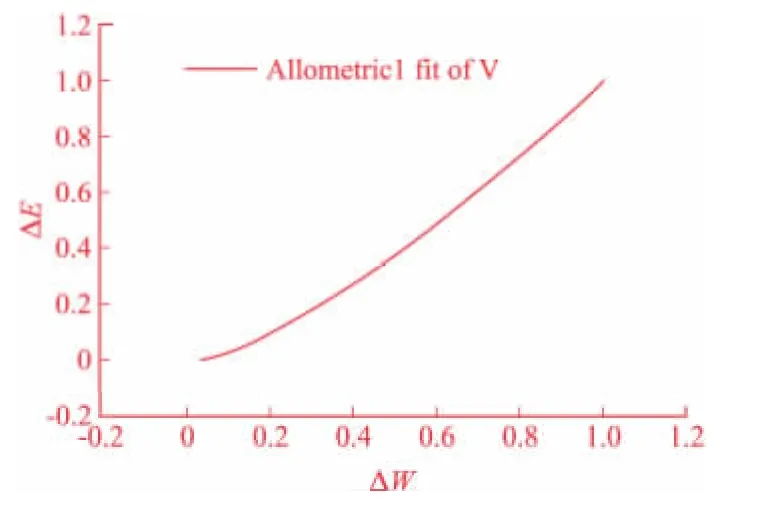
图7 ΔW-ΔE拟合曲线

表4 ΔW-ΔE拟合结果

由表3、表4可知装甲板的易损性和毁伤函数为:

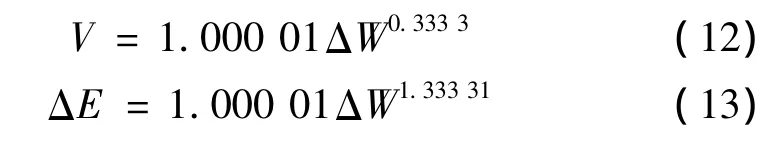
3 讨论

总结上述分析和计算可知，用一定物理和数学含义的表达式来定义目标的结构易损性和毁伤程度具有切实的可计算性和工程实践性。在特定的弹靶系统中，靶板易损性与穿甲体穿甲效能、靶板毁伤程度与穿甲体穿甲效能的关系都可以通过计算(试验)数据拟合而得到确定的函数表达式。这样就把本质为离散过程的穿甲弹威力试验研究转化为对在某一区间上表达式确定且连续的函数性质的研究，为穿甲弹毁伤效能的研究提供了数学的支持。

［1］R.Germershausen.现代武器弹药技术手册［M］.王雨时，李奎武，等译.北京:兵器工业出版社，1992:50－52.

［2］李向东，杜中华.目标易损性［M］.北京:北京理工大学出版社，2013:1.

［3］巩建兴，玛宝华，刘小玲.目标易损性的概念空间分析［J］.北京理工大学学报，1994，14(4):367－369.

［4］王凤英，刘天生.毁伤理论与技术［M］.北京:北京理工大学出版社，2009:195.

［5］北京工业学院八系.爆炸及其作用:下册［M］.北京:国防工业出版社，1979:205－206.