方形截面导弹气动特性数值研究*

李 剑，李 斌，敬代勇

(中国空空导弹研究院，河南洛阳 471009)

0 引言

大量的战术导弹采用了圆形截面弹体设计，而非圆形截面弹体的研究和应用也越来越多。非圆形截面弹体相对于圆形截面弹体在某些方面具有独特的优势，例如在气动性能的改善，子弹的装填和分离，与发射平台的匹配，隐身性能等［1］。非圆形截面弹体有可能成为未来战术导弹替代圆形截面弹体的较好选择。方形截面弹体应用于未来导弹更是具有独特的优势［2］:

首先，方形截面弹体可以产生相比相同截面面积的圆形截面弹体大得多的法向力;第二，方形截面弹体有利于弹药的装填和携带;第三，方形截面弹体与圆形截面弹体较为接近，无需改变原有的分系统舱段设计;第四，舵面可以高效地折叠，有利于内埋武器舱的装填携带;第五，方形截面弹体可以采用“××”形的舵、翼面布局形式。另外，采用非圆形截面弹体设计已经成为隐身导弹外形设计的重要趋势，与圆形截面弹体相比，方形截面的RCS会大大的降低，显著的降低了导弹的被捕获概率［3］。

为了研究方形截面导弹的气动特性，设计了舵面位于平面和直角两种布局形式方形截面导弹。通过CFD数值模拟方法分析了两种布局形式方形截面导弹的气动特性，并与常规圆形截面导弹进行了对比。

1 数值计算方法

采用定常三维雷诺平均Navier-Stokes方程作为控制方程组，在笛卡尔坐标系中，其形式［4］为:

式中:Q表示守恒量;F、G和H表示对流项;Fv、Gv和Hv表示粘性项。

控制方程组中对流项采用TVD格式离散，粘性项采用中心差分格式，采用当地时间步长和多重网格技术加速收敛。湍流模型为Menter-SST模型，壁面为绝热无滑移边界条件。

2 计算方法验证

2.1 计算条件

计算模型为尖拱头部方形截面弹体，长细比为13，见参考文献［5］。来流条件:Φ =22.5°，Ma∞=2.5，T0=324.82 K，P0=153.22 kPa，Re/l=1.31 ×107/m，α=14°。采用多块对接网格技术保证网格质量总网格数约为160万，计算网格见图1。

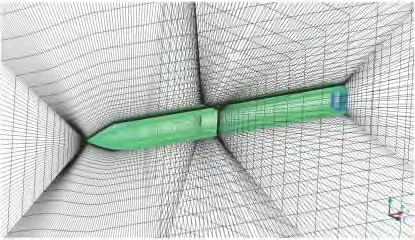
图1 验证模型的计算网格

2.2 计算结果

X=12.5D截面总压云图与蒸汽屏试验［4］对比见图2，从图中可以清晰地看到气流流过弹体后发生分离而产生的两个主涡，计算结果和蒸汽屏试验结果基本一致。X=11.5D截面计算与试验［4］的压力系数分布对比见图3，压力分布计算结果与试验结果符合性较好。

图2 X=12.5D截面总压云图与蒸汽屏试验对比

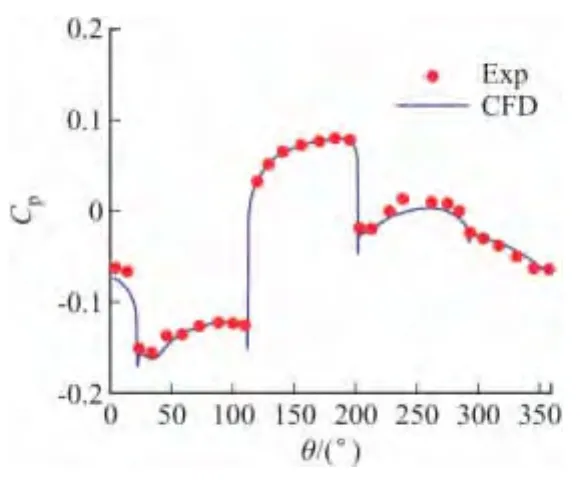
图3 X=11.5D计算与试验的压力分布对比

3 计算模型

方形截面导弹弹体的长细比为20，由尖拱形头部、过渡段、等直段组成，长细比分别为3、3、14。4片舵面呈“×”字形布置。舵面采用了切尖三角形，其中展长1D，梢弦0.5D，根弦1.5D。力矩参考点取全弹长50%位置。

舵面在弹体上的布置方式有两种，一种是舵面位于方形截面的平面上，另一种是舵面位于方形截面的直角上。为了便于比较，还设计了采用相同舵面的圆形截面弹体导弹，见图4。舵面位于“+”字状态定义为 Φ =0°。

图4 方形截面导弹外形

网格划分采用多块结构化网格的方法来将计算区域进行分区，总网格数约为210万。计算状态为:Φ =22.5°，Ma=0.8、2.0，α =0 ～30°。

4 计算结果与分析

4.1 纵向气动特性

Φ =22.5°，Ma=0.8、2.0，δ=0°状态的法向力和俯仰力矩特性分别见图5、图6。从图5中可以看到，方形截面导弹的法向力明显大于圆形截面导弹，尤其是亚音速更为明显。方形截面导弹的两种布局中，舵位于直角的方形截面弹体迎风面积更大一些，因此法向力更大一些。

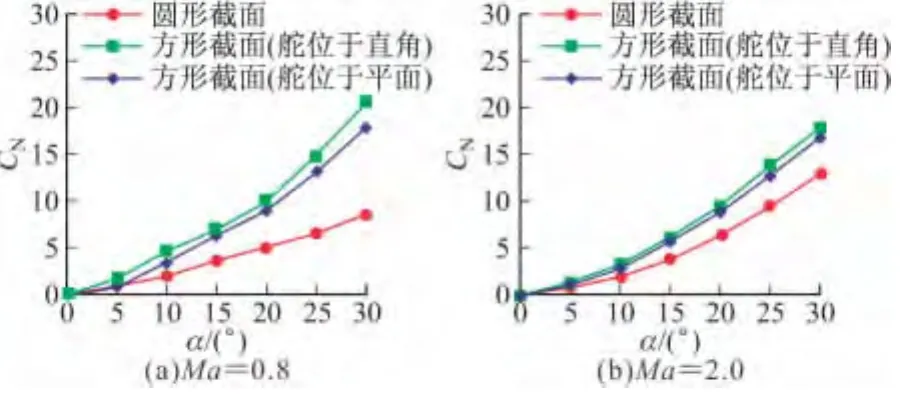
图5 法向力系数随攻角变化(Φ=22.5°)

从图6俯仰力矩曲线可以看到，舵位于直角的方形截面导弹俯仰力矩负值更大一些，舵位于平面的方形截面导弹次之，圆形截面导弹最小。因此，舵位于平面的方形截面导弹具有更大的法向力和负值俯仰力矩。

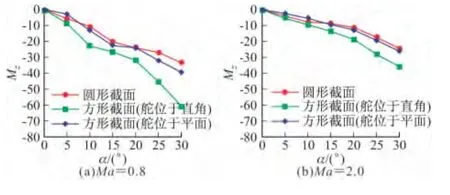
图6 俯仰力矩系数随攻角变化(Φ=22.5°)

4.2 横向气动特性

Φ =22.5°，Ma=0.8、2.0，δ=0°状态的侧向力系数、滚转力矩系数、偏航力矩系数分别见图7～图9。从图7中可以看到，侧向力系数随着攻角增加先增加后减小，在中等攻角下达到最大值，超音速的侧向力系数明显小于亚音速。

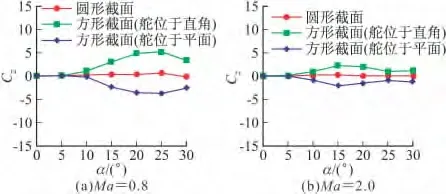
图7 侧向力系数随攻角变化(Φ=22.5°)

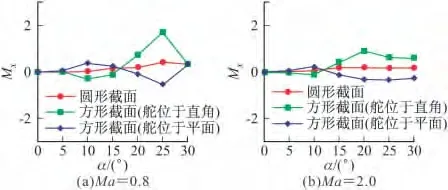
图8 滚转力矩系数随攻角变化(Φ=22.5°)

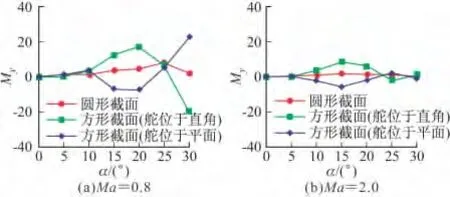
图9 偏航力矩系数随滚转角变化(Φ=22.5°)

从图8可以看到，舵面位于直角的方形截面导弹滚转力矩系数最大，圆形截面导弹最小;超音速的滚转力矩系数明显小于亚音速。

从图9可以看到，舵面位于直角的方形截面导弹偏航力矩系数最大，圆形截面导弹最小;方形截面导弹偏航力矩系数随着攻角增加，先增加后减小，在大攻角时力矩符号发生变化。

从图7～图9中可看到，舵面位于直角和舵面位于平面的侧向力系数、偏航力矩系数、滚转力矩系数的符号都是相反的。这是因为同为滚转22.5°，虽然舵面的滚转方位相同，但是弹体的滚转方位并不同，而弹体对全弹的气动特性影响很大。同时，注意到舵面位于直角布局的横侧向力和力矩系数都大于舵面位于平面布局，这是由于弹体和舵面产生的横侧向力和力矩系数在舵面位于直角布局时是叠加的，而在舵面位于平面布局是抵消的。

4.3 流场分析

图10、图11给出了3种导弹布局在 Φ =22.5°，Ma=0.8、2.0，α =20°的空间流线和截面总压云图。从图中可以看到，气流绕过弹体时从头部已经开始发生分离，产生涡流，随着气流向下游流动，涡的强度不断增加。方形截面弹体由于有4个直角，使得气流极易发生分离，形成分离涡，并且涡强和影响范围也较大，因此方形截面弹体具有较高的法向力。

图10 空间流线和截面总压云图(Ma=0.8，α=20°)

图11 空间流线和截面总压云图(Ma=2.0，α=20°)

由于滚转角22.5°时，方形截面导弹的弹体相对来流左右不对称，因此左、右涡的大小和位置也不相同，从而造成弹体两侧的压力分布不同，产生横侧向力和力矩。舵位于直角和舵位于平面的方形截面导弹在滚转角22.5°时弹体的滚转方位相对攻角平面是对称的，因此弹体产生的涡也呈对称状态。方形的气动特性与滚转角密切相关，在非对称条件下产生非常复杂的背风涡流场，会产生较大的横、侧向气动力。

5 结论

通过以上对方形截面导弹与圆形截面导弹纵、横向气动特性对比和流场分析表明:

1)方形截面导弹的法向力明显大于圆形截面导弹，其中舵面位于平面导弹的法向力大于舵面位于直角导弹。

2)方形截面导弹的横侧向力和力矩相比圆形截面导弹要大得多，其中舵面位于平面导弹的横侧向力和力矩要小于舵面位于直角导弹。

3)方形截面导弹的气动特性与滚转角密切相关，在非对称条件下产生非常复杂的背风涡流场，会产生较大的横、侧向气动力。

［1］Michael J Hemsch.战术导弹空气动力学［M］.北京:宇航出版社，1999.

［2］Trevor J Birch，John R Cleminson.Aerodynamic Characteristics of a Square Cross-Section Missile Configuration at Supersonic Speeds，AIAA 2004-5497［R］.2004.

［2］张昆，薛晓春.截面形状与战术导弹隐身设计［J］.战术导弹技术，2008(2):4－8.

［3］吴颂平，等译.计算流体力学基础及其应用［M］.北京:机械工业出版社，2007.

［4］Floyd J Wilcox，Jr，Trevor J Birch，Jerry M Allen.Force，surface pressure，and flowfield measurements on a slender missile configuration with square cross-section at supersonic speeds，AIAA 2004-5451［R］.2004.