全星历模型下拟Halo轨道设计
2015-12-09杨洪伟李京阳宝音贺西
杨洪伟,李京阳,宝音贺西
(清华大学航天航空学院,北京100084)
全星历模型下拟Halo轨道设计
杨洪伟,李京阳,宝音贺西
(清华大学航天航空学院,北京100084)
本文给出了全星历模型下适用于地月系统和日地系统的拟Halo轨道的设计方法。设计过程以限制三体模型下Halo轨道作为初值并以多点并行打靶法求解全星历模型下拟Halo轨道。采用多点并行打靶法中给出了一类新的可行约束条件,在数值仿真算例中,地月和日地系统L2点附近4圈目标拟Halo轨道均在分钟量级时间内收敛,表明了算法的有效性。
全星历模型;打靶法;Halo轨道;轨道设计
0 引 言
平动点探测任务在深空探测中具有重要意义。人类自发射第一个平动点探测任务航天器ISEE-3[1]以来,已经发射了多个平动点探测任务航天器,包括WIND、SOHO、ACE、MAP、Genesis等[2]。在限制性三体模型下,共线平动点附近存在一类周期轨道-Halo轨道。Halo轨道通常被选作平动点附近探测的飞行轨道。由于Halo轨道是不稳定的周期轨道,需要对其轨道进行保持控制。设计高精度动力学模型下的Halo轨道作为标称轨道,可以降低轨道长期保持所引起的燃料消耗[3]。实际上,由于存在其他行星第三体引力摄动、第二主天体公转轨道偏心率等影响,Halo 轨道在高精度动力学模型下将演化为拟Halo轨道[23]。为研究拟Halo轨道的设计方法,本文采用全星历模型为高精度动力学模型。
限制性三体模型下设计Halo轨道往往采用Richardson三阶近似解[4]作为初值,然后通过微分修正的方法得到Halo轨道。如果以三体模型下得到的Halo轨道作为初值,在全星历模型下作轨道积分,飞行轨道在Halo轨道附近保持一定时间后即发散。为了进一步设计全星历模型下的拟Halo轨道,通常有以下两种方法:1)二级微分修正方法[2-3,5],2)多点并行打靶法[6]。本文采用多点并行打靶法。文献[6]给出了打靶求解时采用的两类不同约束条件。不同于文献[6],本文给出了另外一类可行的约束条件。此外本文还给出了拟Halo轨道的设计过程,并分别在地月和日地L2点附近设计了拟Halo轨道以验证设计方法的有效性。
1 动力学模型及坐标系转换
本文采用两种动力学模型,分别为圆形限制性三体模型和全星历模型。记有效势能
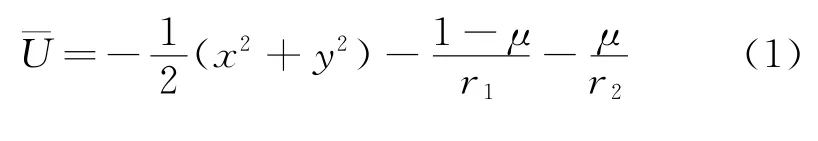
则圆形限制性三体模型下动力学方程为[7]

其中:x,y,z为旋转坐标系下位置坐标;μ为主天体质量比;r1和r2分别为探测器与两个主天体之间的距离
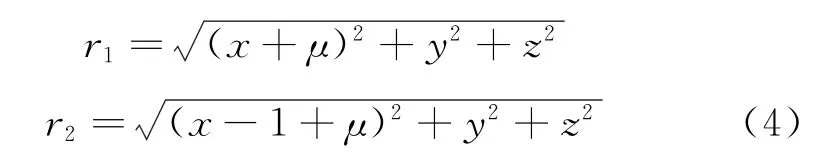
在全星历模型下,太阳系天体的位置和速度通过读取JPL的星历(如DE421)获得。下面以地月系统情形为例,以地球为中心天体,其他天体引力作用考虑为第三体引力摄动[8],建立J2000地球平赤道坐标系下探测器全星历模型如下
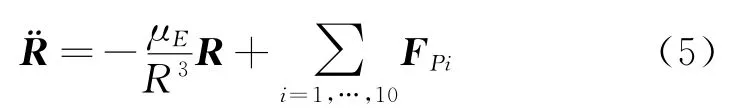
其中:μE为地球引力常数;FPi表示月球、太阳以及其他八大行星/行星系统的第三体引力摄动。
下面根据文献[9],给出以上两种动力学模型中坐标的转换关系。读取JED时刻月球在地球惯性系中的位置RM和速度VM。进行以下计算就可以由归一化的旋转坐标系中的量rsyn与vsyn转换为地球惯性系中的量R与V。
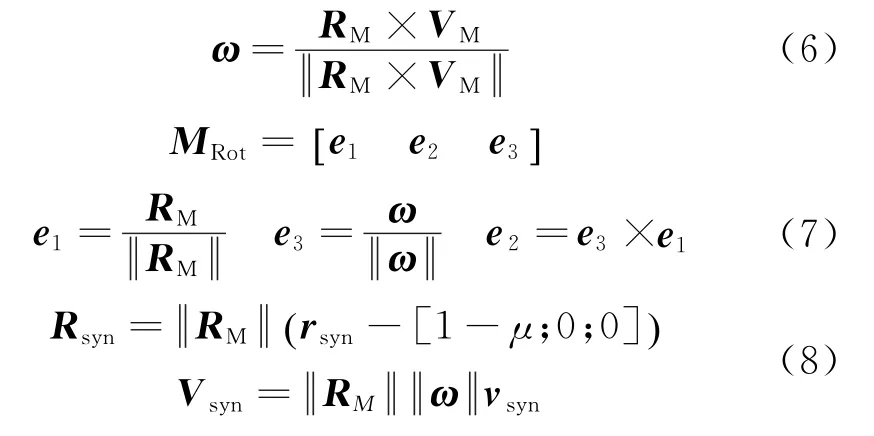
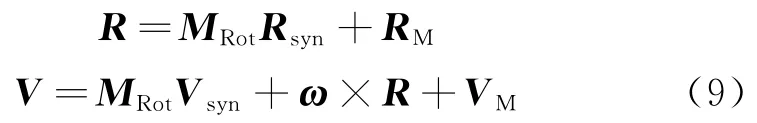
惯性系中的量转换为旋转系中的量为上述过程逆过程,此处省略。
2 拟Halo轨道设计方法
在限制性三体模型下设计Halo轨道一般采用Richardson三阶近似解[5,10]作为初值,然后通过微分修正方法[2,11]即可得到Halo轨道。图1为地月L2点附近的一族Halo轨道及其中一条Halo轨道在各个方向的投影。
真实情况下,由于第二主天体绕第一主天体的轨道并非为圆形,并且探测器在飞行过程中还受到其他天体的引力作用,因此以限制性三体模型设计的Halo轨道作初值,在全星历模型下运行轨道将迅速发散。选取Halo轨道上的10个点做初值,在全星历模型下积分到一个点时刻,如图2所示。虽然积分时间很短,但是也可以明显看到轨道不再闭合。
因此,需要进一步修正三体模型得到的Halo轨道从而得到全星历模型下的拟Halo轨道。求解方法采用多点打靶法[6],但本文的取点方式和约束条件设置与文献[6]有所不同。如图2所示按等长时间间隔选取Halo轨道上N个点,固定这些点的时刻,这样一共有6N个待修正变量。第一类约束条件为第k个点积分到第k+1个点处于k+1个点的状态量重合。根据这类约束条件可以得到以下6N-6个条件

图2 限制性三体模型设计值在不同动力学模型下积分结果.Fig.2 Results of integrating different dynamical modelswith values designed by restricted three-body model
为建立打靶方程,还需要补充6个约束条件。这6个约束条件并没有严格的规定,需要人为合理的设置。本文采用的第二类约束条件如下
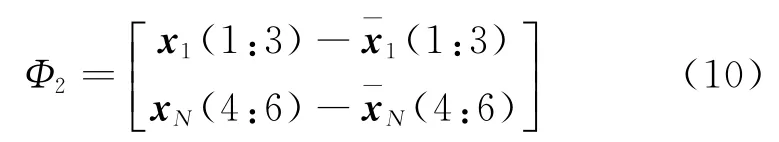
即初始点的位置与末端点的速度与标称情况相同。
结合这两类约束条件可以写出求解所需多点打靶方程
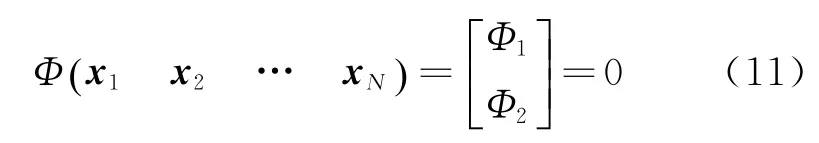
求解式(11)表示的非线性方程可以采用高效的非线性方程求解器MinPack-1[10]。
3 拟Halo轨道设计方法
仿真算例研究地月系统L2点附近拟Halo轨道设计。选取起始时间为2017年5月1日00:00:00,振幅选取为10 000 km,设计轨道圈数为4圈,结果分别如图3和图4所示。为了实现显示效果,图3是在瞬时L2点附近绘制的,其归一化长度单位也是随地月距离变化而改变的。
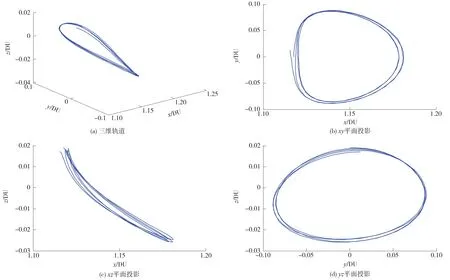
图3 全星历模型下地月L2点附近拟Halo轨道设计结果Fig.3 Quasi Halo orbits around L2 point of the Earth-Moon system by the fullephemeris model
仿真算例研究日地系统L2点附近拟Halo轨道设计。选取起始时间为2021年1月1日0时0分0秒,振幅选取为18×104km,设计轨道圈数为4圈,总时长大约为2年,结果图5所示。

图4 全星历模型下地月L2点附近拟Halo轨道在J2000地球平赤道坐标系中投影Fig.4 Projection of the quasi Halo orbit around L2 of the Earth-Moon system by the full ephemeris model in J2000 Earth equatorial frame
以上算例运行环境为使用i5-4210M CPU和4.0GB内存的个人笔记本电脑,求解程序采用FORTRAN语言编写。打靶求解全星历模型下地月L2点附近拟Halo轨道迭代次数为22次,运行时间为72.322 s;求解全星历模型下日地L2点附近拟Halo轨道迭代次数为29次,运行时间为36.036 s.
求解日地系统和地月系统圈次较少(4圈)的拟Halo轨道仅需要分钟量级的时间就可以收敛。本文所给的算法可以作为工程实际中设计拟Halo轨道一种可选的方法。
需要进一步指出的是,本文所用的方法应用于地月系统时,如果计算拟周期轨道圈次较多时(如50圈),由于太阳的强摄动作用下全星历模型与限制性三体模型差异过大而无法收敛[6]。

图5 全星历模型下日地L2点附近拟Halo轨道设计结果Fig.5 Quasi Halo orbits around L2 point of the Sun-Earth system by the full ephemeris model
4 结 论
本文给出的含新的多点并行打靶法约束的拟Halo轨道设计方法,适用于地月系统和日地系统。仿真算例中,分别设计了地月系统和日地系统L2点附近的拟Halo轨道。结果表明,利用本文提出的算法设计较少圈次的拟Halo轨道可以在分钟量级的时间收敛,可以作为工程应用的一种可选的算法。
[1]Richardson D L.Halo orbit formulation for the ISEE-3 mission[J].Journal of Guidance,Control,and Dynamics,1980,3(6):543-548.
[2]李明涛.共线平动点任务节能轨道设计与优化[D].北京:中国科学院研究生院(空间科学与应用研究中心),2010.[Li M T.Low energy trajectory design and optimization for collinear libration points missions[D].Beijing:Graduate School of Chinese Academy of Sciences(Center for Space Science and Applied Research),2010.]
[3]钱鍴婧,荆武兴,刘癑,等.地月平动点拟周期轨道设计方法[J].系统工程与电子技术,2014,36(8):1586-1594.[Qian Y J,Jing W X,Liu N,et al.Design of quasi-periodic orbit about the translunar libration point[J].Systems Engineering and Electronics,2014,36(8):1586-1594.]
[4]Richardson D L.Analytic construction of periodic orbits about the collinear points[J].Celestial Mechanics,1980,22(3):241-253.
[5]Howell K C,Pernicka H J.Numerical determination of Lissajous trajectories in the restricted three-body problem[J].Celestial Mechanics,1987,41(1-4):107-124.
[6]Gerard G,Jorba A,Simo C,et al.Dynamics and mission design near libration points,Vol I:fundamentals:the case of collinear libration points[M].Singapore:World Scientific Publishing Co Pte Ltd,2001.
[7]Koon W S,Lo M W,Marsden J E,et al.Dynamical systems,the three-body problem and space mission design[J].Available online accessed,2008,21:9.
[8]Battin R H.An introduction to the mathematics and methods of astrodynamics[M].Washington D.C.USA:American Institute of Aeronautics&Astronautics,1999.
[9]Kolemen E,Kasdin N J,Gurfil P.Multiple poincarésections method for finding the quasiperiodic orbits of the restricted three body problem[J].Celestial Mechanics and Dynamical Astronomy,2012,112(1):47-74.
[10]MoréJ J,Garbow B S,Hillstrom K E.User guide for MINPACK-1,CM-P00068642[R].Argonne:National Laboratory,1980.
[11]陈杨.受复杂约束的深空探测轨道精确设计与控制[D].北京:清华大学,2013.[Chen Y.Deep space exploration trajectory design and control in high-fidelity model[D].Beijing:Tsinghua University,2013.]
通信地址:北京市清华大学蒙民伟科技大楼N904(100084)电话:(010)62773402
E-mail:yanghw.happy@163.com
Quasi Halo Orbit Design in Full Ephemeris Model
YANG Hongwei,LI Jingyang,BAOYIN Hexi
(School of Aerospace Engineering,Tsinghua University,Beijing 100084,China)
A method of designing the quasi Halo orbits in the full ephemeris model,which can be applied in both the earth-moon system and sun-earth system,is presented.In the design process,a Halo orbit designed in the restricted three-body model is taken as initial guess,and then a multiple shooting method is used to design in the full ephemeris model.A new feasible constraint condition is given.By numerical simulations,the quasi Halo orbits with four circles are both obtained about one minute for the earth-moon system and sun-earth system respectively,showing the effectiveness of the present algorithm.
full ephemeris model;shooting method;Halo orbit;orbit design
V412.4+1
A
2095-7777(2015)04-0333-05
10.15982/j.issn.2095-7777.2015.04.006
杨洪伟(1989—),男,博士生,主要研究方向:深空探测轨道设计与优化。
[责任编辑:高莎]
2015-09-28
2015-10-17
