广义严格对角占优矩阵的一组含参数充分条件

肖丽霞，韩贵春

(内蒙古民族大学 数学学院，内蒙古 通辽028000)

广义严格对角占优矩阵(非奇异H－矩阵)在计算数学、数学物理、经济学、控制论等领域发挥着重要作用．近年来，对广义严格对角占优矩阵判别方法的研究已取得了一系列研究成果［1－9］．本文所提出的判别方法是在文献［1］和文献［5］的基础上进行了改进，得到了新的含参数的充分条件．

设矩阵A=(aij)∈Cn×n为n阶复(实)方阵，N={1，2，…，n}，α∈［0，1］，记:

定义1［2］设，若存在α∈［0，1］，使得，则称A为α－对角占优矩阵，记为

定义2［2］设，若存在α∈［0，1］，使得，则称A为严格α－对角占优矩阵，记为A∈D(α)．

定义3［2］设A=(aij)∈Cn×n，若存在正对角矩阵X，使得AX∈D(α)，则称A为广义严格α－对角占优矩阵，记为A∈D*(α)．

引理1［2］设A=(aij)∈Cn×n，若A∈D(α)，α∈［0，1］，则A∈D*．

引理2［3］设A=(aij)∈Cn×n，若A∈D0(α)，α∈［0，1］，A不可约且N1≠∅，则A∈D*．

引理3［2］设A=(aij)∈Cn×n，若A∈D0(α)，α∈［0，1］，且∀i∈N3，都有非零元素链aik1，ak2k3，…，akpj，使得j∈N1，则A∈D*．

引理4［4］设A=(aij)∈Cn×n，若存在正对角矩阵X，使得AX∈D*，则A∈D*．

1 主要结果

令α∈［0，1］，为叙述方便，引进下列记号:

其中若N2={j}或N2=∅，令;同理若N1={i}或N1=∅，令

定理1 设A=(aij)∈Cn×n，且N1，N2≠∅，若∀i∈N1，∀j∈N2，满足:

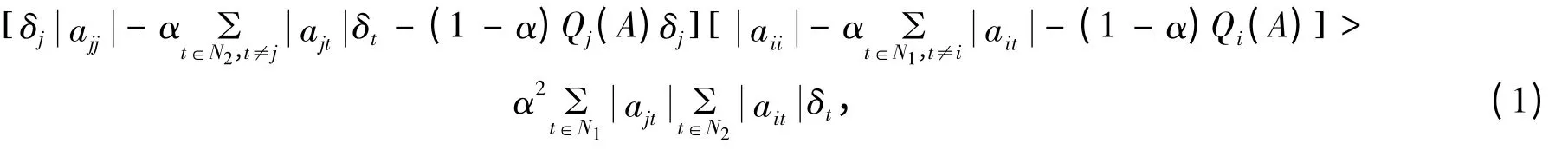
则A为广义严格对角占优矩阵．

证明 令:

构造正对角矩阵X1=diag(d1，d2，…，dn)，并记BAX1=(bij)，其中:

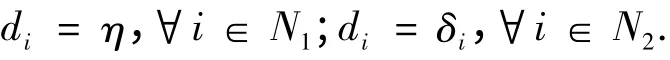
对∀i∈N1，可得:

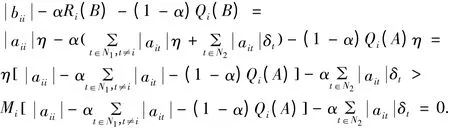
对∀j∈N2，若，根据式(1)可得:

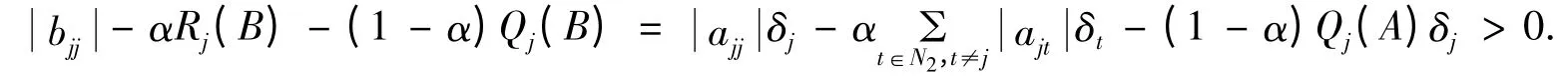
定理2 设不可约矩阵A=(aij)∈Cn×n，且N1，N2≠∅，若∀i∈N1，∀j∈N2，满足:

且上式至少有一个严格不等式成立，则A为广义严格对角占优矩阵．

证明 如同定理1 的证明过程，记Mi，mj，且当时，令mj= +∞． 由式(2)知:Mi≤mj，∀i∈N1，∀j∈N2，因此存在η，使

构造正对角矩阵X2=diag(d1，d2，…，dn)，并记BAX2=(bij)，其中:

类似于定理2 的推证过程可得:

且至少有一个严格不等式成立．又由A不可约，可得B不可约，所以B为不可约α－对角占优矩阵．由引理2可知B=AX2∈D*，其中X2为正对角矩阵，根据引理4，则A∈D*，因此矩阵A为广义严格对角占优矩阵．

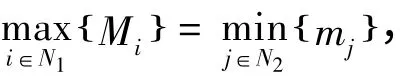
则记N'1={i1，i2，…，il}，N'2={j1，j2，…，jk}，其中N'1⊆N1，N'2⊆N2，Mi，mj如定理1 证明中定义

定理3 设A=(aij)∈Cn×n，且N1，N2≠∅，若∀i∈N1，∀j∈N2，满足:

证明 如同定理2 的证明，可得:

其中:

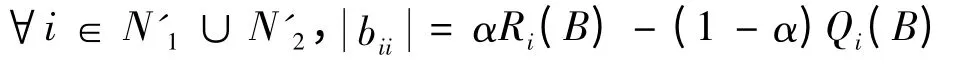
成立，

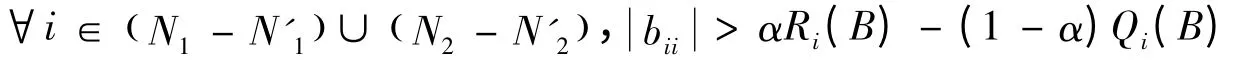
成立，则B为非零元素链对角占优矩阵．根据引理3，B=AX2∈D*，其中X2为正对角矩阵，根据引理4，则A∈D*，因此矩阵A为广义严格对角占优矩阵．

2 数值算例

所以矩阵A满足定理1 的条件，为广义严格对角占优矩阵． 根据文献［1］中定理1，l1=1，r1=2，l2=1，r2=19，因为:

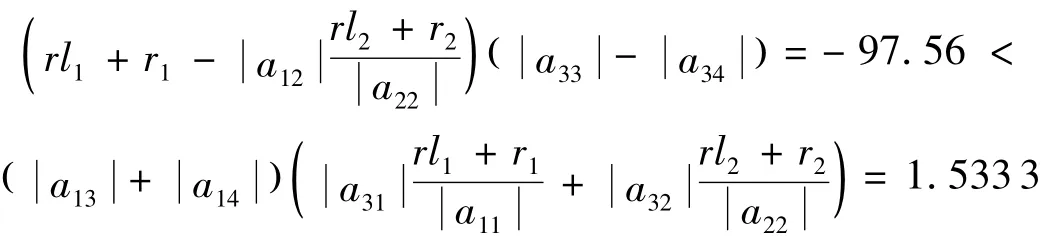
不满足文献［1］中定理1 的条件，所以矩阵A无法用文献［1］中定理1 判定．又因为:

不满足文献［5］中定理2 的条件，所以矩阵A无法用文献［5］中定理2 进行判定．

［1］ 高中喜，黄廷祝．非奇异H－矩阵的充分条件［J］．数学物理学报，2005，25A(3):409－413．

［2］ 孙玉祥．广义对角占优矩阵的充分条件［J］．高等学校计算数学学报，1997，19(3):216－223．

［3］ 谢清明．判定广义对角占优矩阵的几个充分条件［J］．工程数学学报，2006，23(4):757－760．

［4］ Berman A，Plemmons R J．Nonnegative Matrices in the Mathematical Sciences［M］．Philadelphia:SIAM Press，1994．

［5］ 黄廷祝．非奇H矩阵的简捷判据［J］．计算数学，1993，15(3):318－328．

［6］ 孙德淑．非奇异H－矩阵的判定准则［J］．温州大学学报，2009，30(3):18－21．

［7］ 肖丽霞，张俊丽．非奇异H－矩阵新的含参数细分迭代判别法［J］．纯粹数学与应用数学，2014，30(4):386－392．

［8］ 周伟伟，徐仲，陆全，等．非奇H－矩阵的迭代判定准则［J］．工程数学学报，2013，30(5):715－720．

［9］ 张俊丽，韩贵春．非奇异H矩阵的一类判定条件［J］．湖北民族学院学报:自然科学版，2014，32(2):144－147．

［10］ 肖丽霞．非奇异H矩阵新的迭代判定法［J］．湖北民族学院学报:自然科学版，2014，32(4):390－392．

［11］ 杨亚芬，梁茂林．非奇异H矩阵判定的充分条件［J］．苏州科技学院学报:自然科学版，2012，29(3):29－31，50．