深海脐带缆总体响应特性研究
2015-12-09陈希恰宋磊建杜夏英付世晓
陈希恰,宋磊建,杜夏英,万 军,付世晓
(1. 中海石油(中国)天津分公司渤海石油研究院,天津 300452;2. 上海交通大学海洋工程国家重点实验室,上海 200240)
深海脐带缆总体响应特性研究
陈希恰1,宋磊建2,杜夏英1,万 军1,付世晓2
(1. 中海石油(中国)天津分公司渤海石油研究院,天津 300452;2. 上海交通大学海洋工程国家重点实验室,上海 200240)
对某深海脐带缆的总体布局进行了选型设计研究。脐带缆的设计研究正逐渐成为国内海洋工程领域的研究热点,对于脐带缆设计而言总体响应分析是其关键课题。首先推导了悬链线和缓波形两种布局的线型方程。进而基于推导的方程,在有限元软件OrcaFlex中建立了脐带缆悬链线和缓波形两种布局的数值模型,对比分析了两种布局形态下的有效张力和弯曲曲率等响应特性。研究发现相对于悬链线布局,缓波形布局线型较复杂,但能有效降低悬挂点处有效张力。浮力块能有效缓解上部动态响应向触地点处的传播。此外,对缓波形布局中浮子段长度、浮力因子和浮子段起始位置等关键参数对总体响应的影响进行了敏感性分析。所得结论便于设计人员理解脐带缆总体响应特性,选择合适的参数用于脐带缆总体设计。
深海脐带缆;总体响应;悬链线;缓波形;有效张力;弯曲曲率
0 引 言
连接上部浮体和水下生产系统的深海脐带缆,为水下生产系统提供电能、控制信号以及化学药剂,是深海油气开发中的重要装备。随着我国海洋油气开发不断向深海迈进,脐带缆的国产化以及相关基础研究逐渐成为国内海洋工程领域的热点。
深海脐带缆所受到的主要载荷包括自重引起的拉伸载荷和波、浪、流及船体运动引起的动态弯曲载荷。合理的总体布局能够有效降低脐带缆受到的载荷。因此,总体布局设计是脐带缆研究工作中的重要课题。在该领域,众多学者已经开展了大量的研究[1-5]。悬链线布局与缓波形布局是脐带缆常用的两种布局形式。研究表明,在一般水深的作业环境中,由于具有结构简单、施工方便、成本较低和对浮体运动适应能力强等特点,悬链线布局是脐带缆布局形式的首选[6-7]。当水深增加时,随着长度和重量的增加,脐带缆顶部悬挂点处的张力会相应增大,从而提高了对顶部张紧器的要求;当工作环境恶劣时,顶部浮体和波浪运动的动态干扰将会显著地传播到脐带缆触地点处进而引发发脐带缆的疲劳损伤。而采用在脐带缆下半段设置浮力块的缓波形布局形式,可以有效地降低顶部悬挂点处的张力,同时也可缓解上部平台运动和波浪作用对触地点处脐带缆的影响。但相对于悬链线布局,缓波形布局更加复杂,安装和制造费用更高[8-11]。
为了深入了解深海脐带缆在不同布局形式下的结构响应,本文首先推导了悬链线和缓波形两种布局的线型方程。进而基于推导的方程,在有限元软件OrcaFlex[12]中分别建立了脐带缆在悬链线和缓波形两种布局形式下的数值模型。对比分析了两种布局形式下脐带缆有效张力和弯曲曲率的结构响应特性。此外,还对缓波形布局中浮子段长度、浮力因子和浮子段起始位置等关键参数对脐带缆总体响应的影响进行了敏感性分析。
1 总体布局线型理论推导
脐带缆空间线型是其总体响应分析的基础。基于锚链的悬链线方程,可推导获得脐带缆悬链线布局和缓波形布局理论公式。
1.1 悬链线布局
图1为悬链线线型示意图,其空间坐标位置表达式为
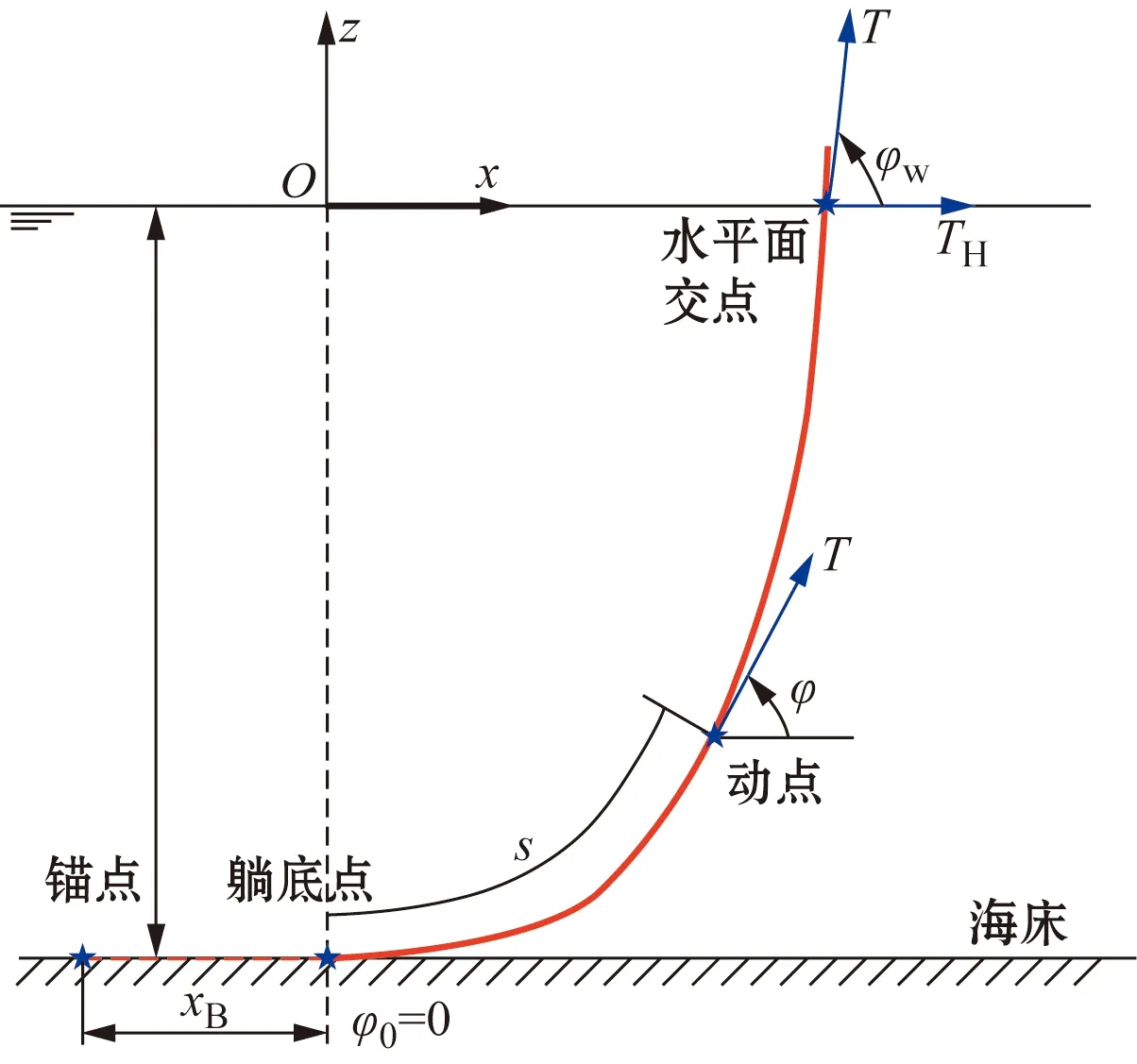
图1 悬链线布局线型示意图Fig.1 Shape of the free hanging catenary
式中:TH为悬挂点的水平张力;φw为顶部悬挂角;h为悬挂点处水深;W为管线单位长度湿重。
由式(1)和式(2)可知,获得顶部悬挂角、悬挂点处水深和管线单位长度湿重三个参数,即可确定脐带缆任意一点的位置坐标。
1.2 缓波形布局
缓波形布局总体线型分布如图2。整条脐带缆可以分为悬垂段AC、浮子段CE、下降段EF以及触地段FP。其中悬垂段可以分为悬挂段AB和跳接段BC;浮子段可以分为上升段CD和拖曳段DE;下降段为EF。图2中的S1、S2、S3、S4和S5表示的是各段脐带缆的长度;x1~x5和y1~y5分别为悬挂段AB、跳接段BC、上升段CD、拖曳段DE和下降段EF的水平跨距和垂直长度。
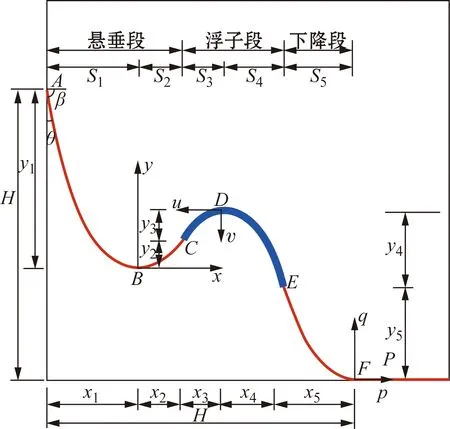
图2 缓波形布局线型示意图Fig.2 Shape of the lazy wave
缓波形布局中,悬挂段AB、跳接段BC、升举段CD和拖曳段DE以及下降段EF均可看作悬链布局。根据悬链线方程可以得到缓波形线形空间坐标理论公式[3]:
式中:αB、αD和αF分别为点B、点D和点F处的曲率。
根据悬垂段AC、浮子段CE、下降段EF的长度S12、S34和S5,各段单位长度湿重W12、W34和W5,可计算出各段的x、y坐标以及αB、αD和αF:
式中:n为浮力因子,其计算公式为
式中:Wf为CE段浮力块提供的浮力。
脐带缆缓波形布局设计中,一般给出的参数包括:顶部悬挂点处水深h,顶端悬挂角θ,管线单位长度的湿重W,悬垂段长度S12,浮子段长度S34以及浮力因子n。下降段的长度S5是未知的。因此,为了得到缓波形的线型布局,需要进行迭代计算[3]。具体计算过程如下:
(1) 假定S5=S0。
(2) 将S5代入式(4)即可得到αB、αD和αF。
(3) 利用式(5)计算得到x1~x5和y1~y5。
(4) 根据公式H=y1+y4+y5-y2-y3得到H。
(5) 当|H-h|/h<0.1%时,终止计算;否则,令S5=S0+ΔS,重复步骤(2)~(5)。
将各参数的计算结果代入式(3)即可获得缓波形线型空间位置坐标。
2 数值模型建立
脐带缆结构组成由内到外层次分明,如图3所示,外层构件以一定的角度螺旋缠绕于内层构件上,外层与内层的构件采用非粘结方式接触,从而导致脐带缆具有多层、多接触、可滑动的特性。虽然脐带缆的结构组成非常复杂,但其总体力学行为与结构构造简单的立管相类似,因此在总体响应分析时可将脐带缆等效为结构组成单一的钢制管道[13]。表1所示为某脐带缆等效结构参数。

图3 深海脐带缆结构Fig.3 Components of deep-sea umbilical
针对表1的脐带缆进行悬链线布局和缓波形布局设计,表2给出了脐带缆在两种布局下的基本布局参数。

表2 悬链线布局和缓波形布局基本参数Table 2 Main parameters of the free hanging catenary shape and the lazy-wave shape
基于表1和表2中的参数,根据式(3)和式(5)可分别计算出脐带缆悬链线布局和缓波形布局的空间位置坐标。进而,在有限元软件OrcaFlex中建立脐带缆两种布局下的总体模型,如图4和图5所示。脐带缆采用Line单元建立而缓波形中浮子段采用Line with Floats单元模拟。假设脐带缆躺底段平铺于海底,其与海底的作用采用线性假设理论,土壤的垂直刚度为100 kPa/m2,土壤与脐带缆的切向摩擦系数为0.5。脐带缆的顶端悬挂于浮体底部,底端固定在海底井口处,连接处均可自由转动。

图4 悬链线布局有限元模型Fig.4 Finite element model of the free hanging catenary
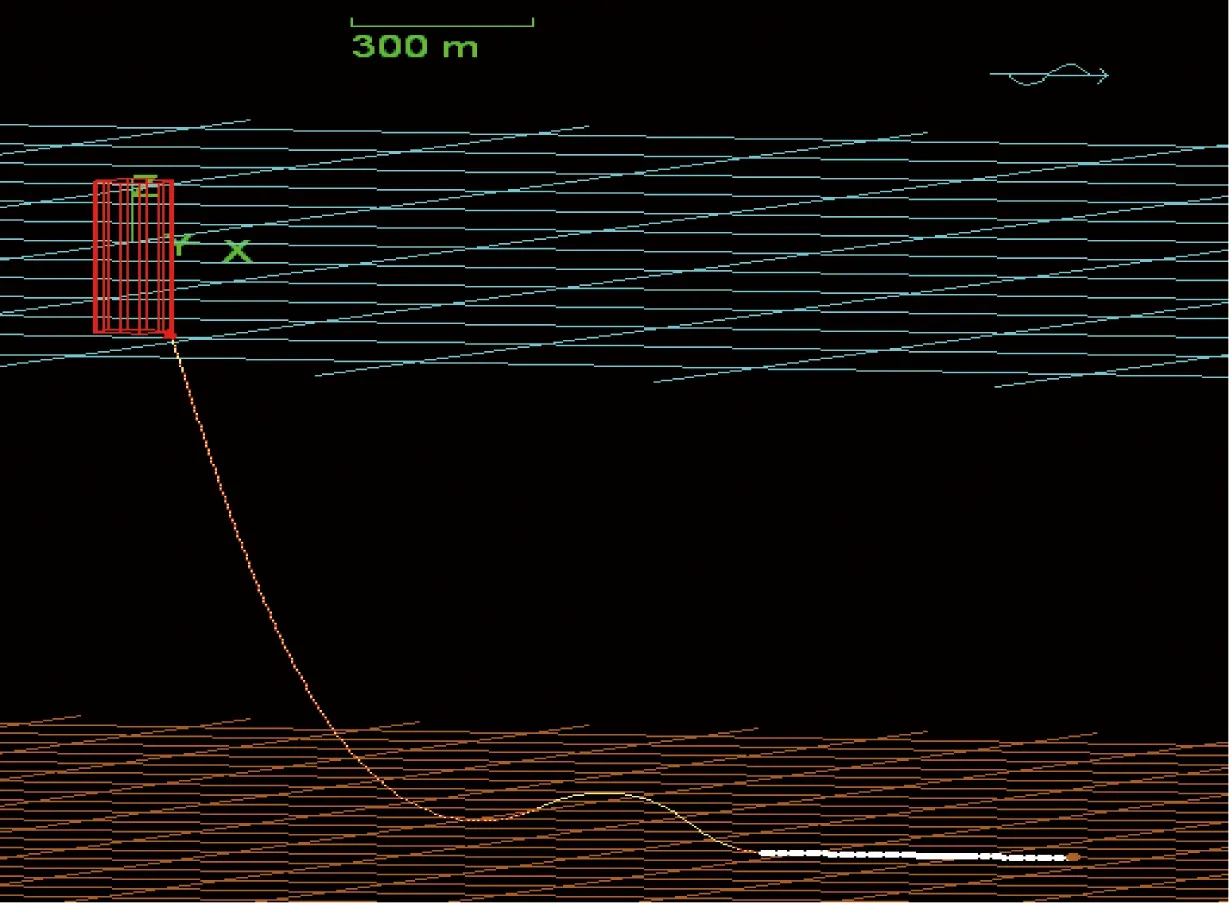
图5 缓波形布局有限元模型Fig.5 Finite element model of the lazy wave
3 悬链线和缓波形布局总体响应对比
3.1 静态响应对比
利用建立的数值模型,分别计算脐带缆在悬链线和缓波形两种布局下的静态结构响应特性,结果对比如图6和图7所示。
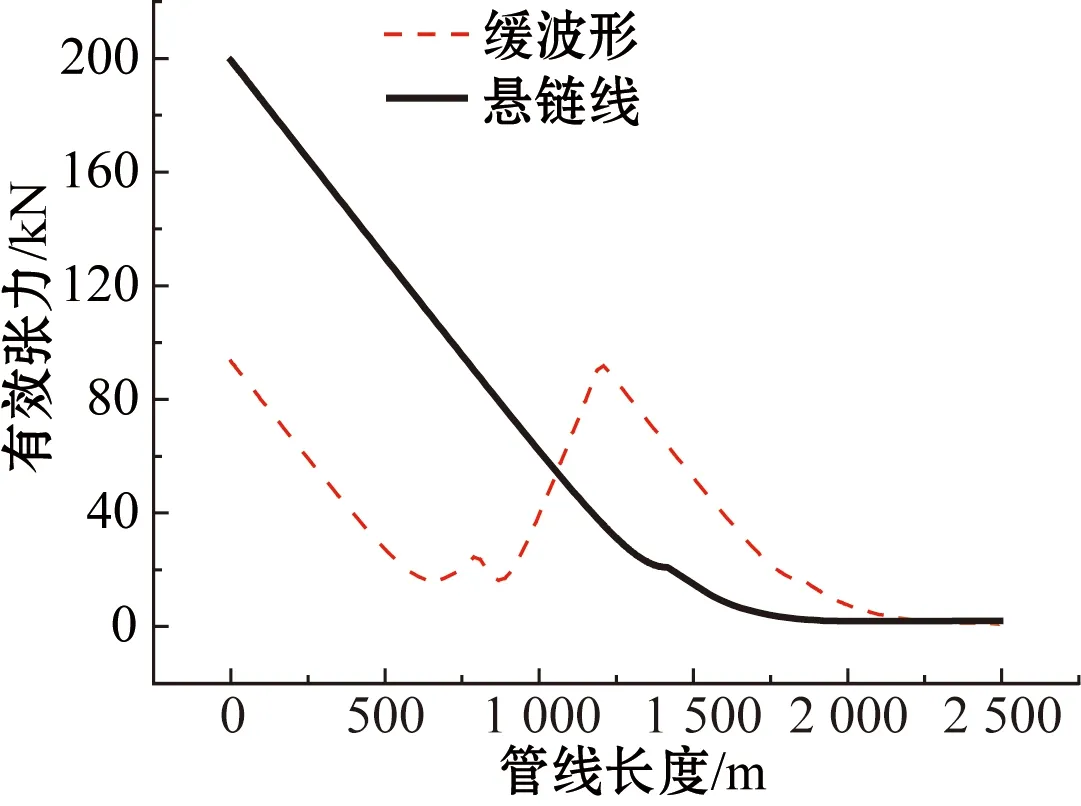
图6 静态有效张力分布对比Fig.6 Comparison of static effective tension
图6为脐带缆两种布局下有效张力对比图。由图可见,悬链线布局下有效张力沿着脐带缆长度方向不断减小;而对于缓波形布局,由于浮子段浮力作用,有效张力先减小、再增大最后又减小,导致有效张力在浮子段末尾点出现一个极大值。同时,两种布局下脐带缆有效张力的最大值均发生在顶部悬挂点,且悬链线布局有效张力最大值明显大于缓波形布局有效张力的最大值。因此,当水深增加到一定深度后,脐带缆采用悬链线布局满足不了张力设计要求时,可以选用缓波形布局。
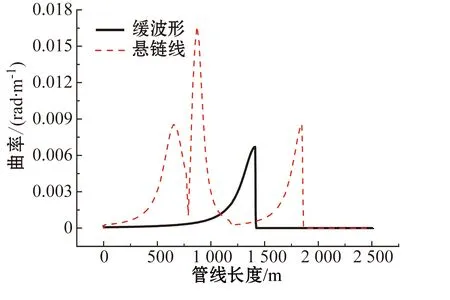
图7 静态弯曲曲率分布对比Fig.7 Comparison of static bending curvature
图7为脐带缆在悬链线布局和缓波形布局下的弯曲曲率响应。由图可知,悬链线布局下脐带缆弯曲曲率最大值发生在触地点处,而缓波形布局下弯曲曲率的最大值发生在浮子段上升段的末端,且缓波形布局形式下的最大弯曲曲率大于悬链线布局形式的。这是由于浮子段处产生拱形线型,造成了较大的局部弯曲。因此,在脐带缆缓波布局设计时,应该注意浮力块参数的选取,避免产生较大的局部弯曲。
3.2 动态响应对比
分别计算脐带缆两种布局在表3中环境条件下的动态响应,对比结果如图8~11所示。

表3 环境参数Table 3 Environment parameters
图8为悬链线脐带缆动态有效张力分布图。从图中可以看出,顶部浮体的运动以及波浪载荷对整体脐带缆的有效张力分布均有影响,其中对脐带缆顶端张力的影响最大,越往下越小。而如图9所示,外部动态扰动对缓波形脐带缆悬垂段部分的有效张力有较大的影响,对浮子段及其以下部分则几乎没有影响。

图8 悬链线脐带缆动态张力分布图Fig.8 Dynamic effective tension of the free hanging catenary
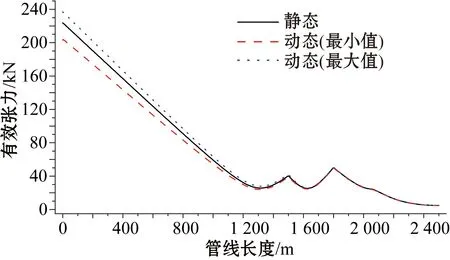
图9 缓波形脐带缆动态张力分布图Fig.9 Dynamic effective tension of the lazy wave
图10为悬链线脐带缆动态弯曲曲率分布图。外部扰动对脐带缆上弯曲曲率的影响主要集中在顶部悬挂点区域以及触地点区域,而对悬垂段和躺地段处的弯曲曲率影响很小。弯曲曲率的极值出现在顶部悬挂点和触底点上,而对于顶部悬挂点出现的弯曲曲率极值,可以通过在脐带缆的悬挂点处安装抗弯装置(Bend stiffer)来解决。
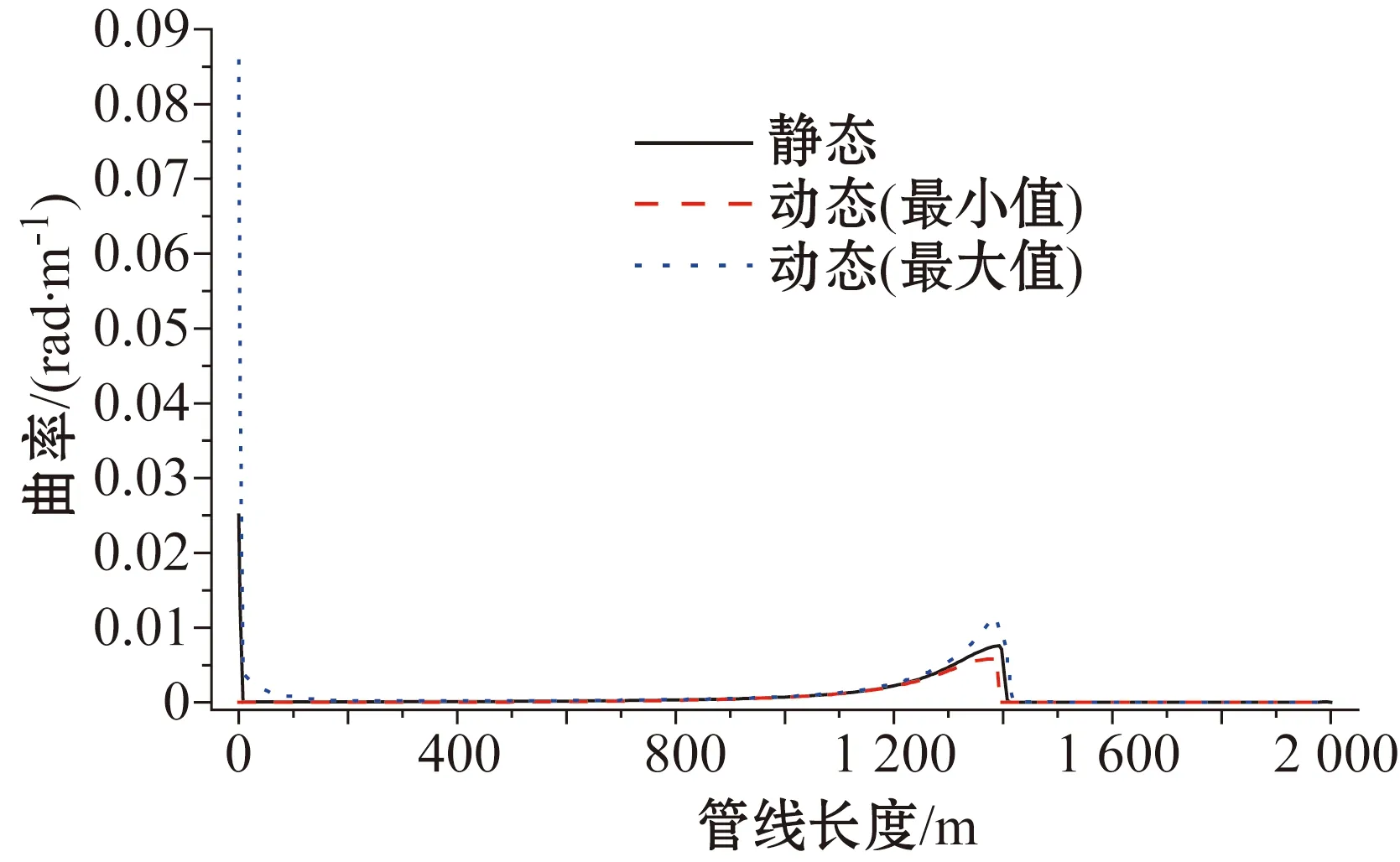
图10 悬链线脐带缆动态曲率分布图Fig.10 Dynamic bending curvature of the free hanging catenary
相对于悬链线布局,缓波形布局动态响应主要集中在顶部悬挂点区域,其余部分包括触地点处的弯曲曲率所受影响很小,如图11所示。对于顶部悬挂点出现的弯曲曲率极值,可以通过在悬挂点处安装抗弯装置来缓解。

图11 缓波形脐带缆动态曲率分布图Fig.11 Dynamic bending curvature of the lazy wave
4 缓波形布局参数敏感性分析
缓波形布局形式较为复杂,影响其线型分布的因素很多。下面对缓波形布局脐带缆总体响应进行敏感性分析,分析浮子段长度、浮力因子和浮子段起始位置对脐带缆总体响应的影响。
4.1 浮子段长度敏感性分析
分别计算浮子段长度为200 m、300 m、400 m和500 m时脐带缆的总体响应。对应的有效张力和弯曲曲率分布如图12和图13所示。

图12 不同浮子断长度下弯曲曲率分布对比Fig.12 Comparision of bending curvature for different lengths of buoyancy catenary

图13 不同浮子断长度下有效张力分布对比Fig.13 Comparison of effective tension for different lengths of buoyancy catenary
如图12所示,浮子段越长,脐带缆上最大的弯曲曲率以及触地点处的弯曲曲率也越大。对于有效张力而言,如图13所示,随着浮子段的增长,顶部悬挂点处的有效张力减小,而浮子段末尾处以及下降段上的有效张力增大。这是因为由于浮力的增大,减小了脐带缆对悬挂点处张力的需求,然而由于浮力增大,使得立管的下降段增长,从而使得浮子段末尾和下降段上的有效张力变大。
4.2 浮力因子敏感性分析
浮力因子的大小表征了单位长度浮力块提供的浮力大小。为了研究浮力因子对脐带缆整体线形性能的影响,保持其他参数不变,计算当浮力因子为2、3、4时脐带缆的静态响应,得到脐带缆的弯曲曲率和有效张力分布如图14和图15所示。
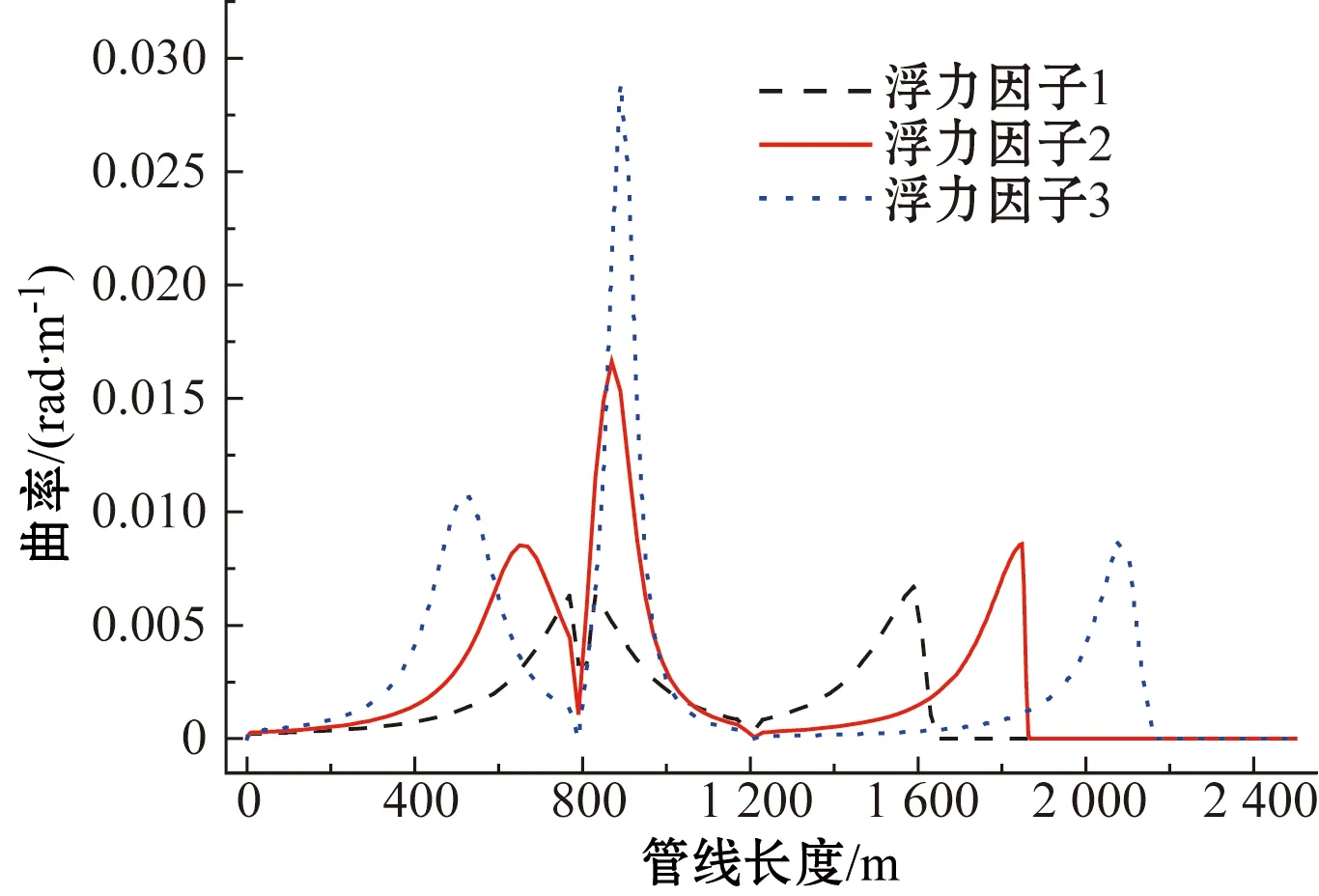
图14 不同浮力因子下弯曲曲率分布对比Fig.14 Comparison of bending curvature for different float factors
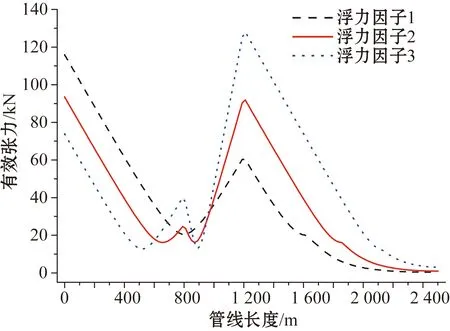
图15 不同浮力因子下有效张力分布对比Fig.15 Comparison of effective tension for different float factors
如图14所示,浮力因子越大,脐带缆最大弯曲曲率以及触地点处的弯曲曲率也越大。对于有效张力而言,如图15所示,浮力因子的大小对缓波形脐带缆有效张力的分布有很大的影响。当浮力因子增大时,顶部悬挂点处的有效张力减小,而浮子段末端的有效张力增大。这符合实际情况,因为浮力因子越大,浮子段提供的浮力也越大,从而减小对顶部悬挂点处张力的需求。同时,浮力因子越大,缓波形脐带缆下降段的长度也越大,使得下降段对浮子段末尾处的拉力增大,从而使得浮子段末尾处的有效张力变大。
4.3 浮子段起始位置敏感性分析
浮子段起点距顶部悬挂点的距离,即浮子段的起始位置,对缓波形脐带缆的初始形状和静态响应有很大的影响。为了研究浮子段起始位置的参数敏感性,在保持其他参数不变的情况下,计算浮子段起始位置分别为700 m、800 m、900 m、1 000 m和1 500 m时缓波形脐带缆的总体响应,得到有效张力以及弯曲曲率,如图16和图17所示。
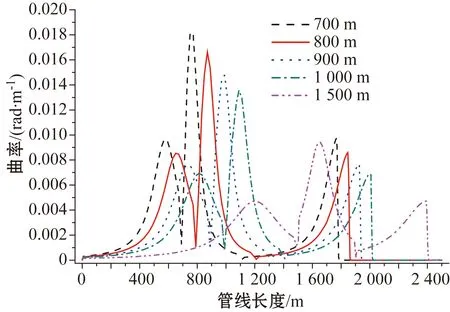
图16 不同浮子段起始位置下弯曲曲率分布对比Fig.16 Comparison of bending curvature for different starting locations of the buoyancy catenary
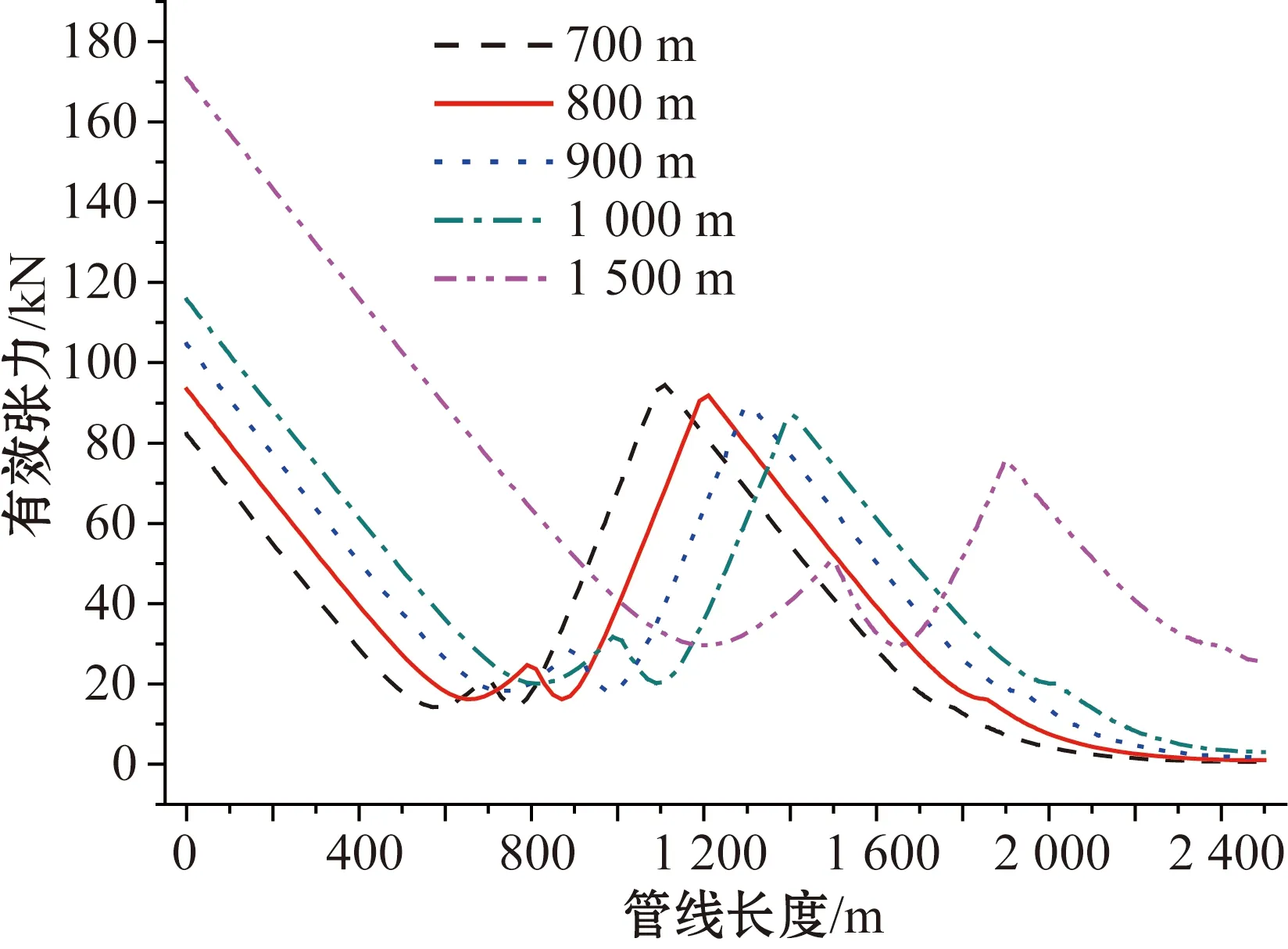
图17 不同浮子段起始位置下有效张力分布对比Fig.17 Comparison of effective tension for different starting locations of the buoyancy catenary
图16所示为不同浮子段起始位置下脐带缆的初始线型。由图可以看出,浮子段起始位置值越大,脐带缆顶部悬挂点距底部触地点之间的跨距越大,脐带缆的波形越缓。同时,随着浮子段起始位置值的增大,最大弯曲曲率逐渐减小。对于有效张力,由图17可知,随着浮子段起始位置值变大,悬挂段长度变大,从而导致悬挂点处的有效张力变大,同时由于浮子段起始位置值变大,下降段的长度变小,从而导致浮子段末端处的有效张力减小。
5 结 语
本文基于数值软件OrcaFlex计算并对比了脐带缆悬链线和缓波形两种布局形态下的总体响应结果,讨论了浮子段长度、浮力因子和浮力块起始位置对缓波形脐带缆总体响应的影响。得到如下结论:
(1) 相对于悬链线布局形态,缓波形布局下脐带缆线型更为复杂,然而由于浮子段的作用,可以有效降低悬挂点处的有效张力,故而缓波形适合应用于作业水深较深、悬挂点处张力较大情况,且浮力块可以有效降低上部动态响应向底部触地点处的传播。
(2) 浮子段长度和浮力因子对缓波形脐带缆总体线形的影响是一样的,增大浮子段的长度或增大浮力因子都会使脐带缆的波形变陡,最大弯曲曲率变大,但会减小脐带缆的最大有效张力,并使得悬垂段处的有效张力减小,浮子段末尾处及下降段上的有效张力增大;同时增大浮子段起始位置会使脐带缆的波形变缓,减小脐带缆的最大弯曲曲率,却增大其最大有效张力。
[1] 黄维平,白兴兰,李华军.国外深水钢悬链线立管研究发展现状[J].中国海洋大学学报,2009,39(2):290.
[2] 谢彬,段梦兰,秦太验,等.海洋深水立管的疲劳断裂与可靠性评估研究进展[J].石油学报,2004,25(3):95.
[3] 宋磊建,付世晓,陈希恰,等.深海脐带缆总体响应特性比较研究[J].振动与冲击,2014,33(1):119.
[4] da Silveira L M Y, Tanaka R L, Novaes J P Z. Rayleigh damping effects on global analysis of umbilicals[C]. OMAE, 2011: 49584.
[5] Qiu W, Cao Q, Librino F, et al. Global design and analysis of umbilical in offshore applications[C]. OMAE, 2009: 79841.
[6] Howells H. Advances in steel catenary riser design[C]. DEEPTEC′95, 1995.
[7] Hatton S. Update on the design of steel catenary riser systems[R]. 1999.
[8] Yue B, Walters D, Yu W. Lazy wave SCR on turret moored FPSO[C]. ISOPE, 2011: 16.
[9] 孙丽萍,周佳,王佳琦.深水柔性立管的缓波形布置及参数敏感性分析[J].中国海洋平台,2011,26(3):37.
[10] Yang H, Li H. Sensitivity analysis of fatigue life prediction for deepwater steel lazy wave catenary risers [J]. Science China Technological Sciences, 2011, 54(7): 1881.
[11] Li S, Nguyen C. Dynamic response of deepwater lazy-wave catenary riser[C]. DOT International, 2010.
[12] Orcina. OrcaFlex manual: version 9.0a[M]. Cumbria: Orcina, 2006.
[13] International Organization for Standardization. ISO 13628-5. Petroleum and natural gas industries—design and operation of subsea production systems. Part 5: subsea umbilicals[S]. 2002.
GlobalResponseAnalysisfortheDeep-SeaUmbilical
CHEN Xi-qia1, SONG Lei-jian2, DU Xia-ying1, WAN Jun1, FU Shi-xiao2
(1.BohaiOilfieldResearchInstitute,TianjinBranch,CNOOCChinaLimited,Tianjin300452,China;2.StateKeyLaboratoryofOceanEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)
We present the global analysis for the deep-sea umbilical. The design and analysis of the umbilical has become the research focus in the offshore engineering field. Global response analysis is the key issue in the research of umbilical. We present the theoretical models of the free hanging catenary shape and the lazy-wave shape at first. Based on the theoretical models, the umbilical models of the free hanging catenary shape and lazy-wave shape are then developed in OrcaFlex. The distribution characteristics of effective tension and bending curvature are calculated and compared. The results show that the shape of the lazy-wave is more complex than that of the free hanging catenary. However, the lazy-wave shape can reduce the effective tension at the top hanging points and dynamic response at the touchdown point, which makes it more applicable in the deep sea. Meanwhile, the sensitivity analysis of the generalized configuration parameters, including the length of the buoyancy catenary, the buoyancy factor and the starting location of the buoyancy catenary, is performed and the effect of the configuration parameters on the static characteristics of the umbilical is studied. The research results may provide a reference for the configuration design of the deep-sea umbilical.
deep-sea umbilical; global response; free hanging catenary; lazy-wave shape; effective tension; bending curvature
TE52
A
2095-7297(2015)02-0111-07
2015-01-22
陈希恰(1988—),男,硕士,主要从事海洋工程结构物强度与疲劳分析方面的研究。
