提高思维含量 深化数学思考
2015-12-08刘发昌张冬兰
刘发昌 张冬兰

摘要:“数学思考”是数学课程四大目标之一。教师要引领学生经历“数学思考”的探索活动,就得提高“问题”、“材料”、“操作”、“习题”的思维含量,使学生学会数学思考,养成数学思考的习惯。
关键词:思维含量;数学思考
中图分类号:G623.5 文献标志码:B 文章编号:1674-9324(2015)05-0235-02
现代教育理念把“数学思考”列入数学课程四大目标之一。《数学课程标准》总目标中指出:“学生能运用数学的思维方式进行思考”。在专项目标中对“数学思考”作了具体阐述:建立数感、符号意识和空间观念……学会独立思考,体会数学的基本思想和思维方式。用著名学者郑毓信教授的话来讲,数学教学就是通过数学学习,引导学生学会数学思维,引导学生学会数学思考。作为教师,应透过“热闹”的表面对课堂进行理性分析,努力提高课堂教学的思维含量,深化学生的数学思考。
一、提高“问题”思维含量,引发数学思考
问题是数学的“心脏”,是课堂教学的“课眼”,也是课堂教学的主线。有效的问题具有引领、导向的作用。而问题的有效性很大程度就是看它含有多少数学思考的内涵,能否引发不同层次学生的数学思考。例如,教学“三角形三边关系”时,我将导入问题情境稍作改编:
两个问题情境都直接指向数学知识的本质:不同走法的路线围成三角形,不同走法的路程分别是三角形的一条长边和另两条短边之和,这样的情境有利于引导学生将“路程问题”抽象成“三角形三边关系”问题,启发学生对“三角形三边长度关系”的思考。
进一步分析对比,我们发现改编后的问题情境思维含量更高。第一,外延大。两个核心问题:走哪条路最近?走哪条路最远?迫使学生进行两次比较:第一次是大三角形的长边与两条短边之和作比较;第二次是小三角形的长边与两条短边之和作比较。通过一大一小两个三角形的呈现,学生必然思考:是不是所有三角形三边之间都存在这样关系呢?渗透从具体到一般的数学思想方法。第二,问域宽。照顾到不同层次学生差异发展。思维水平较低的学生会思考“走哪条路最近”的问题,而思维水平较高的学生还能思考“走哪条路最远”问题,通过汇报交流产生思维碰撞,使不同层次学生都能得到不同的发展。第三,挑战性强。原情境中的问题,学生凭生活经验或视觉直觉(直路最近)就能即问即答。而改编后的问题,学生必须通过独立思考或同伴互助才能做出相应的回答。
可见,“问题”思维含量的高低,决定学生数学思考的广度和深度。提高“问题”思维含量,应抓住数学的本质,使问题直接指向教学中的主要矛盾,可以从知识的连接点、教学的重难点、学生疑惑点、数学思想的聚焦点等方面设问,丰富问题内涵,拓宽问题的外延,实现以“问”引思,激发不同层次的学生进行独立思考。
二、提高“材料”思维含量,促进数学思考
数学是研究数量关系和空间形式的科学,数学知识具有高度抽象性和概括性,而小学生以形象思维为主,其认知活动需要直观材料作支撑。合理开发、精心制作学具材料要以思维含量的高低为衡量标准。例如,“三角形的三边关系”这课,书中展示的学具材料是三组不同长度的“纸条”。仔细分析,用“纸条”围三角形,探索三边关系有一定的局限性。请看我自制的学具材料:
①黑线段:
②红线段:
制作方法:分别用红黑句号笔在有刻度的透明软垫板沿边画线段,根据需要的长度剪成长条形。
并引导学生对“材料”进行如下剪拼:
1.剪一剪:
①拿出两条黑线段,引导思考:围成三角形要3条线段,只有2条怎么办?(生:剪其中一条)
②为了研究方便,只剪整厘米数,记住自己剪的是长线段还是短线段?
2.围一围:注意端点相连,围在展板上,用磁扣扣好,看是否围成了三角形?
3.再剪围:拿出红线段剪,要求:如果刚才剪长(短)线段,这次剪短(长)线段。
4.展一展: ……
不管是纸条还是线段,其目的都是为了生成“围成”与“围不成”素材,为进一步观察、探究提供物质基础。但自制的学具材料具有独特、丰富的数学内涵。第一,动态化。原材料的数据是给定的、固定的,而自制的材料通过学生动手剪,动态生成不同的数据,因此也比原材料更加开放。第二,精细化。原材料是纸条,改编后是线段。在实际操作中,因纸条有一定的宽度,当它们的长为5、7、12这种情况时,很难用眼睛看出“围不成”的现象,而线段精确、细小,减小了误差,避免了视觉上的错觉。第三,隐含数形结合思想。自制的线段是画在有刻度的软垫板上,数形结合,学生很容易从数据上去分析“围成”与“围不成”的原因。
可见,运用于数学操作的材料不同于工艺材料,不追求外表华丽,而讲究“数学味”。提高“材料”的思维含量,应从知识内容特点,可操作性、数学思想、教学细节等多方面考虑,使得通过材料的操作推动学生进行分析、综合、比较、抽象、概括,深刻理解知识的本质意义。
三、提高“操作”思维含量,学会数学思考
数学课堂,要引领学生亲身经历将操作经验内化为数学经验,就得充分调动学生的手和脑,手脑并用,让外显的动作与内隐的思维紧密结合,使操作活动成为思维的动作和动作的思维。
例如,“平行四边形面积”的教学,开始学生所暴露出来的原生态思维是:底×邻边=平行四边形面积,学生很难想到将它沿高剪拼成长方形来计算的转化方法。为了突破这一难点,我引领学生进行如下操作、思考:
1.拉一拉。
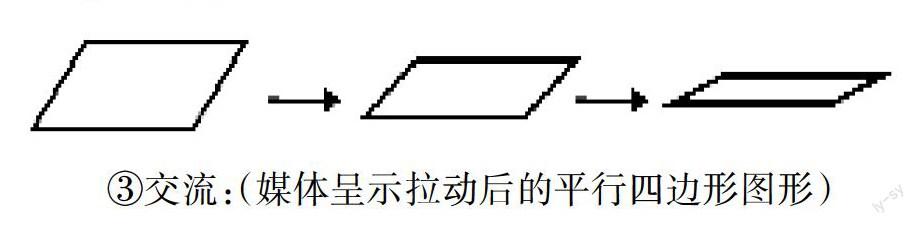
①实践:捏住平行四边形模型的两个对角,往外拉一拉。
②想象:如果把每次拉动后的平行四边形拍下来,比较这几个平行四边形,什么没有发生变化?什么发生了变化?
③交流:(媒体呈示拉动后的平行四边形图形)
……
生1:周长没有变。
生2:底和邻边长度不会变。
生3:面积变小了。
师追问:既然面积变了,那你们刚才的猜想:底×邻边=平行四边形面积,还成立吗?
2.作高。
①实践:在作业纸上分别作出它们的高,观察高有什么变化?
……
②思考:面积为什么变小?面积的大小可能与平行四边形的什么有关?
生1:平行四边形面积可能与高有关。
生2:平行四边形面积可能等于底乘高。
……
3.计算。
师:想办法计算平行四边形的面积,验证你的猜想。
……
案例中,我抓住了知识的生长点,顺着学生思维开展操作活动。在操作中,通过启发想象、组织交流、点拨追问,学生很快发现自己所想的与操作结果不一样,思维产生矛盾冲突。此时学生处于“心求通而未得,口欲言而未达”的愤悱状态。再引导学生分别作出它们的高,观察拉动平行四边形过程中高的变化规律,学生自然调整猜想:平行四边形的面积可能与底和高有关系。再让学生计算平行四边形的面积时,由于学生只学过长方形的面积计算,学生想到“沿高剪拼成长方形”来计算,可谓是水到渠成了,学生不仅“知其然而且知其所以然”。
提高“操作”思维含量,教师应准确把握教学难点,加强操作前、操作中、操作后的启发、点拨、交流活动,使操作活动始终与数学思考有机结合,通过动态操作引发学生的认知冲突,实现以操作启迪思维,以思维引领操作。
四、提高“习题”思维含量,内化数学思考
习题与例题一样,既承载巩固知识、形成技能的功能,也有为学生积累基本的活动经验、明晰数学基本思想、锻炼思维的价值。但长期以来,因习题以静态的测试形式呈现,许多教师、学生仅满足“做题”的层面,使得习题功能弱化,教材意图不能凸显。
提高“习题”的思维含量,就是要透过“做题”表面,挖掘习题背后隐藏的思维内涵为学生所用,通过习题内化学生的数学思考,发展学生思维。
教学中,我不再停留在就题论题的层面上,而是通过有序呈现和巧设不完整结构,给学生提供更广阔的探索、思考空间,不仅深化乘法意义的理解,还培养学生的分析能力和估算意识。
《新课程标准》指出:“独立思考、学会思考是创新的核心”。没有数学思考,就没有真正意义的数学学习。教师要引领学生经历“数学思考”的探索活动,就得提高“问题”、“材料”、“操作”、“习题”的思维含量,使学生学会数学思考,养成数学思考的习惯。
