期权定价方程的紧致差分算法
2015-12-08黄振平
黄振平
(长沙理工大学数学与计算科学学院,湖南长沙410004)
期权定价方程的紧致差分算法
黄振平
(长沙理工大学数学与计算科学学院,湖南长沙410004)
利用紧致有限差分方法进行空间离散,修正龙格库塔方法进行时间离散,建立一种求解期权定价方程的数值格式,较好地解决了对空间与时间混合导数项的离散问题,并在空间和时间上都保持了较高阶精度.所得数值结果证实了该数值格式具有较高的精度.
紧致有限差分方法;修正龙格库塔方法;期权定价方程;数值解
引言
期权定价领域的开创性工作是由Black和Scholes在1973年中,在通过求解一个抛物型欧式期权偏微分方程(俗称Black-Scholes方程)时发现的.该模型在学术界引起强烈反响,对投资者如何对期权定价和风险对冲都产生了重大影响,并且对之后的衍生工具发展起到了决定性的作用.
目前已经有各种有限差分方法[1]研究了Black-Scholes方程.有限差分法的一个主要缺点是随着逼近阶的增加,计算量也相应扩大.1992年,Lele总结Pade格式[2],得到了任意高阶精度对称紧致有限差分格式的推导方法,高阶紧致有限差分法考虑的是函数值和它的在每个离散点处未知的一阶二阶导数.对比有限差分格式,该方法,在相同网格点下,可以给出更高的精度和解的特性,此特性使他们更接近光谱方法,例如使用五个节点即可达到六阶精度[3].该方法的应用十分广泛,曾经被用来研究弹性波方程、泊松方程、N-S方程等.
本文利用紧致有限差分方法进行空间离散,修正Runge-Kutt方法进行时间离散,建立一种求解期权定价方程的数值格式,较好地解决了对空间与时间混合导数项的离散问题,并在空间和时间上都保持了高阶精度.所得数值结果证实了该数值格式具有较高的精度.
1 紧致差分方法介绍
紧致有限差分方法是使用函数值的某种线性组合来表示该函数导数值的线性组合的一类差分方法,该方法增加了差分格式的精度与稳定性.
1.1 空间离散,构造三点六阶精度紧致差分格式[3]:
对于区间[a,b]上的函数f(x),考虑节点为x0,x1,…,xN的均匀网格,步长h=xi+1-xi,i=0,1,…,N-1.节点处的函数值为vi,一阶和二阶导数值分别为v′i和v″i.现在开始构造均匀网格上的三格点六阶精度紧致差分格式.
文献[4]中,作者采用特殊紧致差分格式来推导二阶导数:用三个连续点处的函数值和它的一阶导数值来近似位于同样三点处的二阶导数值,该二阶导数值具有六阶精度.借用这个想法,我们得出以下混合问题的六阶差分格式,具体的推导过程可参照文献[5].
对于内点,二阶导数值与函数值之间满足关系:
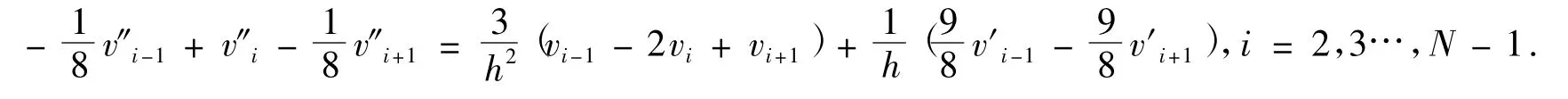
对于边界点处的二阶导数构造如下格式:
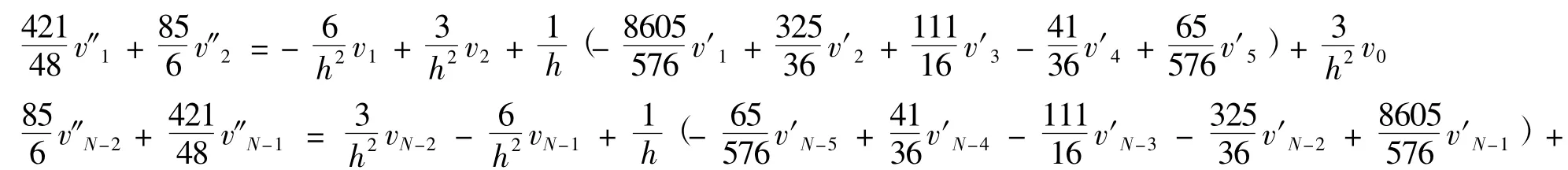
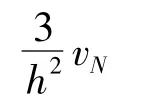
联合上面三式,写成矩阵形式:
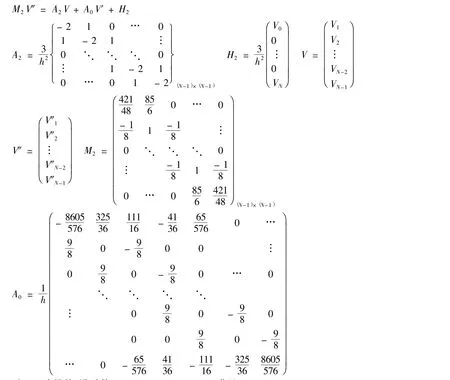
对于一阶导数,设系数ai-1,ai,ai+1,mi-1,mi+1满足:
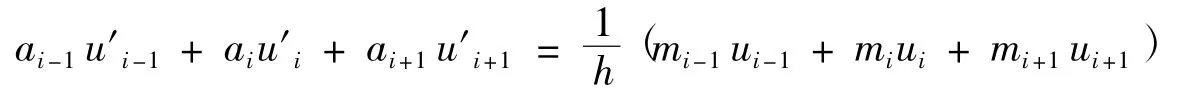
将上式两端分别在xi点进行Taylor展开,结合六阶精度,得到系数线性方程组,解之,得如下三点六阶紧致格式,具体推导可以参考[5].
对于内点xi,一阶导数值与函数值之间满足关系:
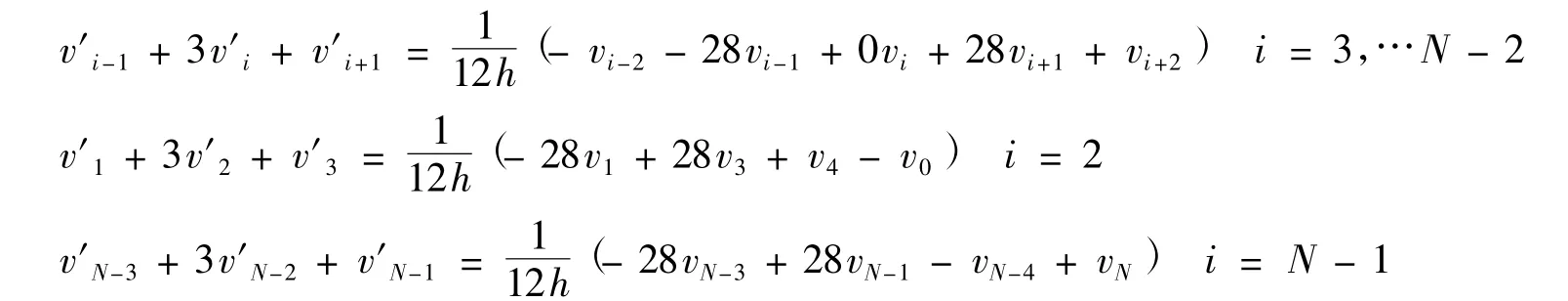
对于边界点处的一阶导数构造如下格式:
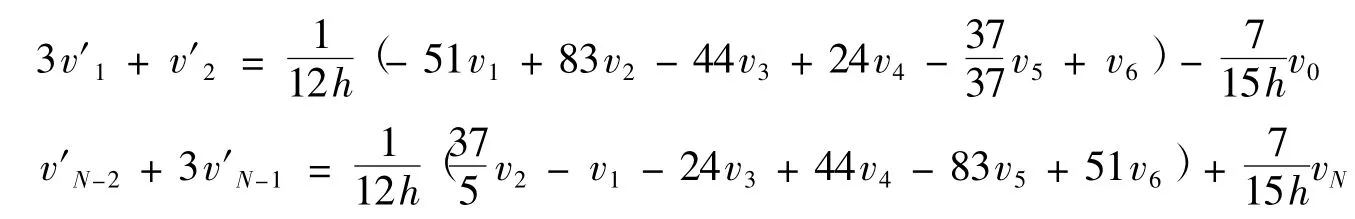
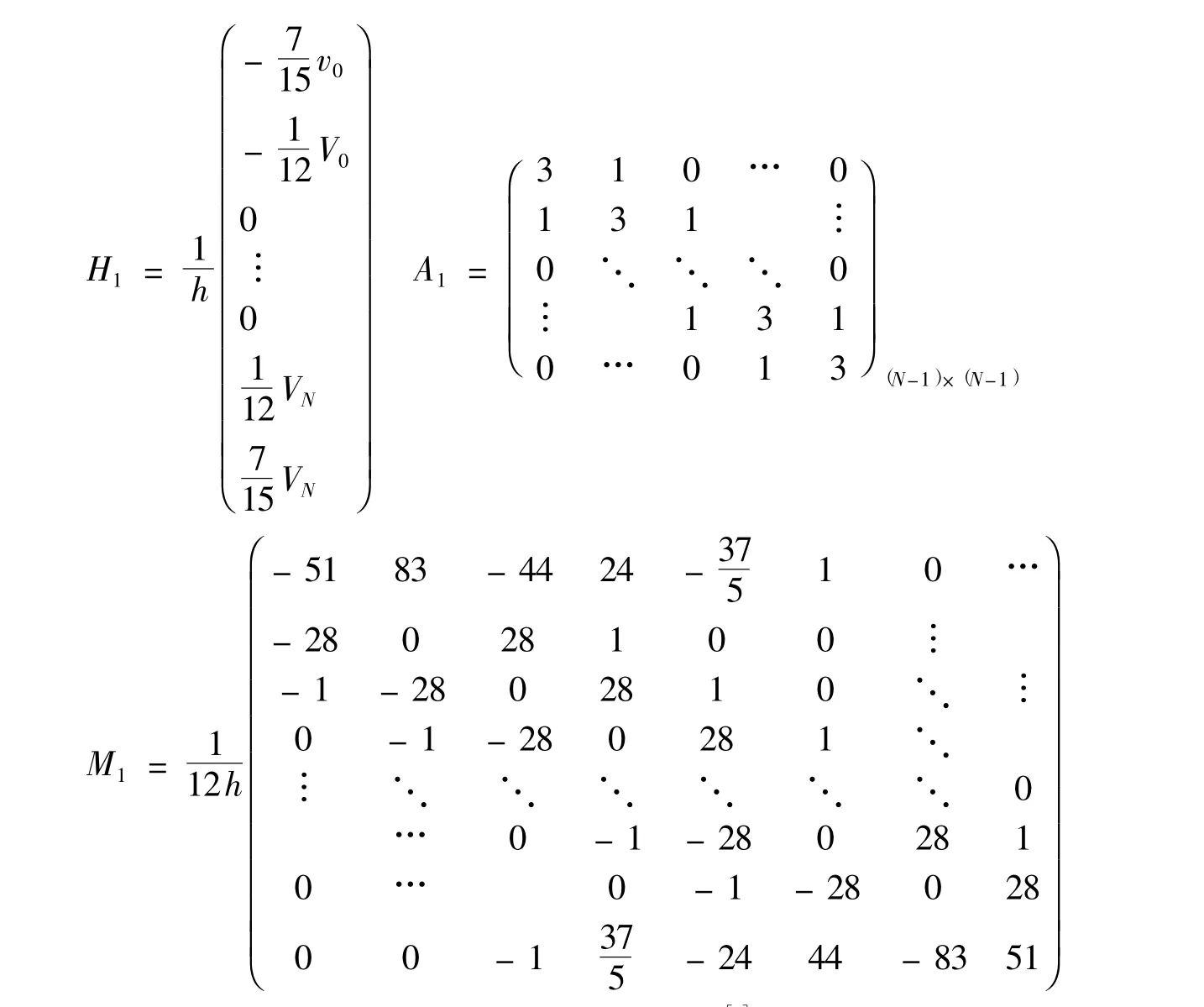
将上述五式写成矩阵形式:A1V′=M1V+H1
1.2 时间离散,使用修正Runge-Kutta方法[6]:
为了提高计算效率,减少内存的占用,本文使用了同样具有4阶精度的修正Runge-Kutta格式.
修正Runge-Kutta格式显式推进计算公式如下:
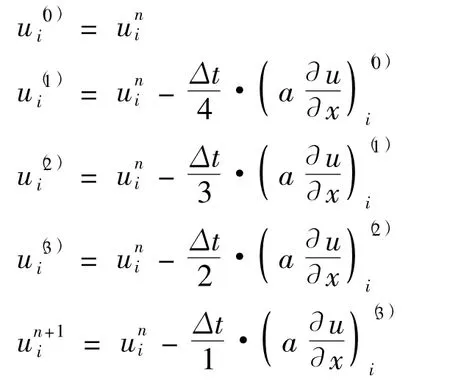
四步时间推进使得4阶修正Runge-Kutt.格式具有4阶精度,格式具有较高的稳定性,使得显式时间推进能够取到较大的时间步长,加快计算收敛的速度.
2 紧致差分算法解期权定价方程
用v(s,t)表示期权价格,则欧式看涨期权模型满足如下Black-Scholes方程
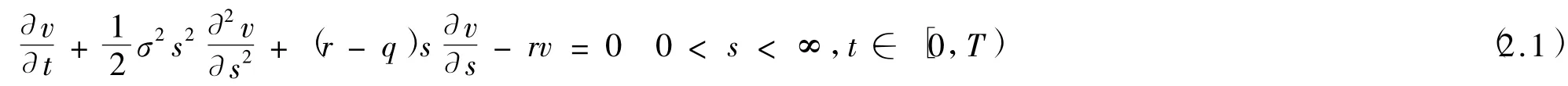
初值条件

边界条件
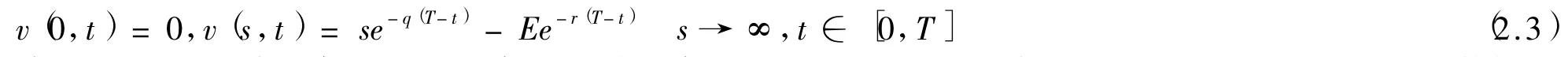
其中:是R无风险利率,q是红利率,σ是波动率,T是到期日,E是敲定价格,方程(2.1)是一个变系数倒向抛物型方程,(2.1)—(2.3)是一个倒向定解问题.
做变换

可以将欧式期权模型(2.1)—(2.3)转化为常系数对流扩散方程的定解问题
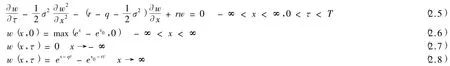
其中x0=ln E
为了习惯方便,下面以u(x,t)表示期权价格,t=τ.下面是用紧致的差分方法,通过matlab来求解方程(2.5).
等距网格剖分:
对于空间变量x,计算区域取为有限区域Ω=(xmin,xmax).空间和时间网格节点分别为Ωh={xi=xmin+(i-1)h,i=1,2,…,M+1,h=(xmax-xmin)/M}
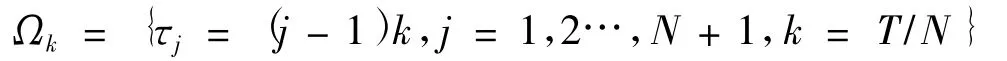
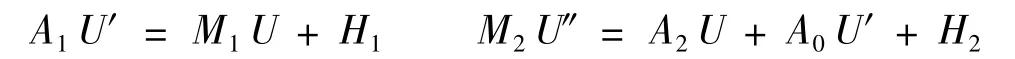
若知道u在x=xi,i=2,…,M处的值,通过matlab软件,由雅可比迭代可以求得对应各节点处的一阶和二阶导数值
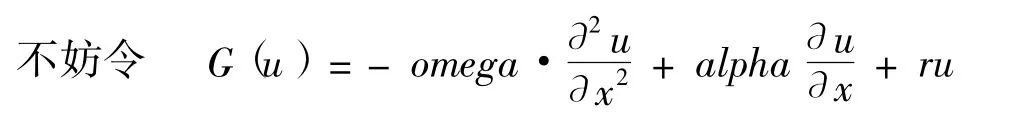
则x=xi,i=2,…,M,t=tn时,由修正Runge-Kutt方法得:
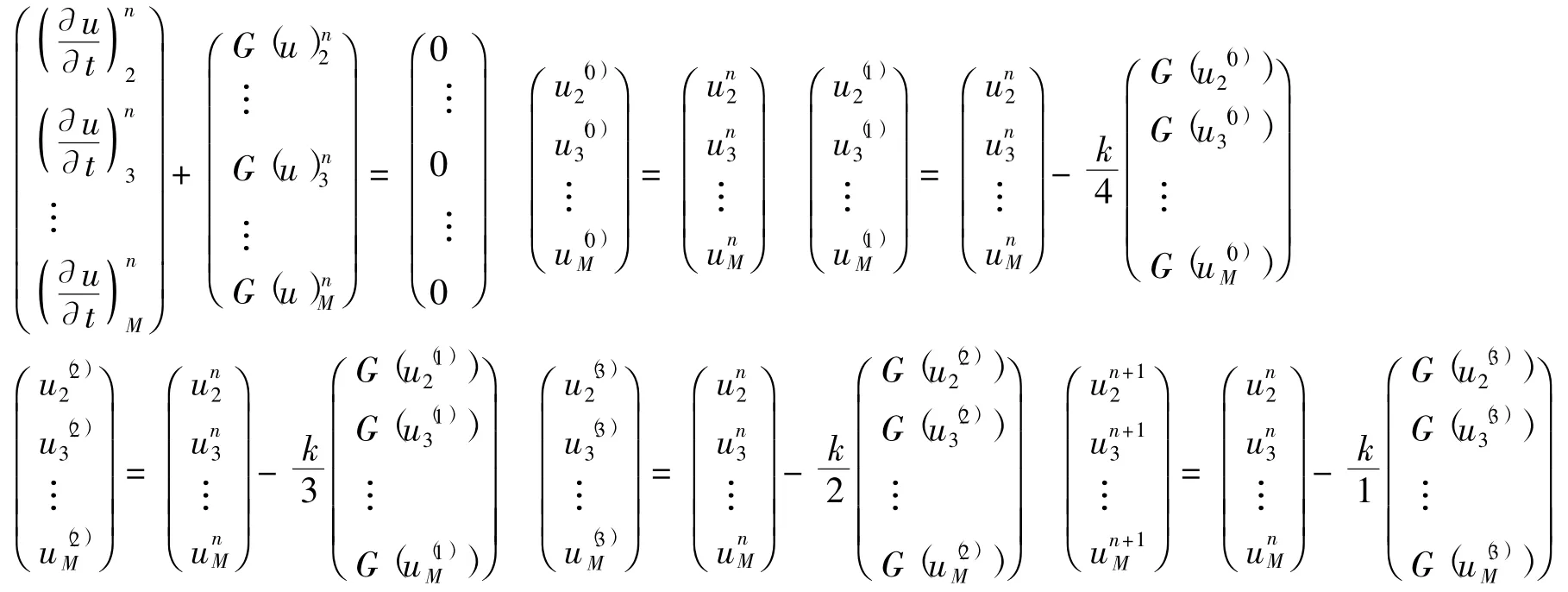
于是结合初边值和第n层的一阶,二阶导数,由第n层u的函数值可推出第n+1层的函数值,不断迭代,继而求出t=T层的函数值.
具体方法详见篇尾的matalab程序代码.
3 数值实验
这一节中,我们通过MATLAB,利用紧差分格式进行数值试验,表中e1表示T时刻精确解和数值解的误差,分别表示e1在T时刻的误差二范数和无穷范数.对空间变量x,M等分后步长为h,对时间变量t,N等分后步长为k.下图横坐标为In(x),纵坐标为log10|e1|,x1为左端点,x2为右端点.
算例1:参数取值是:r=0.05,q=0.2,σ=0.3,E=2,T=0.25,N=1600.

算例2:参数取值是:r=0.05,q=0.2,σ=0.3,E=2,T=0.25,N=1600,M=160

算例3:r=0.05,q=0.2,σ=0.3,E=2,N=1600,M=160,s1=0.2,s2=400

表1 紧致差分格式的误差范数
综上述,边界处误差比较大,可能源于该格式边节点处精度略有下降有关,但经过实验数据对比,整体上该方法是稳定可行的,接下来将会继续改进.
[1]刘铭辉.欧式看涨期权定价微分方程的有限差分求解方法[M].哈尔滨:哈尔滨工业大学,2012:11-18.
[2]LELE SK.compact finite difference schemes with spectral-like resolution[J].Journal of computationnal Physics,1992(103):16-42.
[3]Jichao Zhao.Highly accurate compactmixedmethods for two pointboundary value problems[J].elsevier,2006(188):1402-1417.
[4]P.C.Chu,C.Fan,A three-point combined compact difference scheme,J.Comput.Phys,1998(140);370-399.
[5]Shukla,R.K.,!Zhong,X.:Derivation of high-order compact finite difference schemes for nonuniform grid using polynomial interpolation.J.Comput.Phys,2005(204):404-429.
[6]沈露予.不可压缩Navier-Stokes方程高精度算法研究[D].南京:南京信息工程大学,2005:8-100.
Compact Difference Algorithm for the Option Pricing Equation
HUANG Zhen-ping
(Changsha University of Science and Technology,Changsha,Hunan 410004)
Acompact difference scheme is established for solving the option pricing equation by using the the compact finite differencemethod in space discretization and themodified Runge-Kuttamethod in time discretization.Themixed derivative is skillfully treated and the high order accuracy ismaintained both in space and time.It is confirmed that the numerical schemes obtained from the scheme have high accuracy.
compact finite difference method;modified Runge Kutta method;option pricing equation;numerical solution
O155
A
1671-9743(2015)11-0018-06
2015-10-21
黄振平,1985年生,男,湖南郴州人,硕士研究生,研究方向:偏微分方程数值解.
