图的Fractional边全控制
2015-12-08徐保根赵丽鑫
徐保根,赵丽鑫,邹 妍
(华东交通大学理学院,江西 南昌 330013)
图的Fractional边全控制
徐保根,赵丽鑫,邹 妍
(华东交通大学理学院,江西 南昌 330013)
设G=(V,E)是一个无孤立边的图,一个实值函数f:E(G)→[0,1]若对所有的边e∈E(G),均有成立,则称f为图G的一个Fractional边全控制函数。图G的Fractional边全控制数定义为为图G的一个Fractional边全控制函数}。确定了一般图的Fractional边全控制数若干界限,同时也研究了几类特殊图Fractional边全控制问题,给出了一些特殊图的Fractional边全控制数。
Fractional边全控制函数;Fractional边全控制数;Fractional边全包装函数;Fractional边全包装数
1 引言及定义
本文中所指的图均为无向简单图,符号和术语同于文献[1-2]。
图的控制理论是图论中很重要的一个分支。在图的控制理论的发展和完善过程中,Hedetniemi S M等人首次提出并研究了图的Fractional控制概念和性质,在当MITCHELL S和HEDETNIEMI S T引入了图的一般边控制的概念之后,自然产生了图的Fractional边控制概念,并对其进行了大量研究[3-4]。 而文献[5]首先提出并研究了图的符号边控制,由此衍生到边上的多种控制概念,如Fractional边控制等[6]等,从而使得控制理论的研究内容和研究成果越来越丰富,本文主要给出了图的Fractional边全控制概念和一些主要结果。
设G=(V,E)是一个连通图,用V(G)和E(G)分别表示G的顶点集和边集。对于任意一条边e∈E(G),定义e在G中的邻域NG[e],表示G中与边e相关联的边的集合。闭边邻域NG[e]=NG(e)∪{e}。NG(e)和NG[e]分别简记为NG(e)和NG[e]。v点G在中的度记为d(V)=|N(v)|,并且△=△(G)和δ=δ(G)分别表示图G中点的最大度和最小度,边e在图G中的边度是指与其相连的边的条数,记为d(e)=│N(e)│。若e=uv∈E(G),则有d(e)=d(u)+d(v) -2。△′=△′(G)和δ′=δ′(G)和分别表示图G中边的最大度和最小度。
为了方便,设G=(V,E)若S⊆E(G),f:E→R为一个实值函数,则记

定义1[7]设G=(V,E)是一个无孤立边的图,如果一个实值函数f:E→[0,1]对任意的e∈E(G)均有f(N(e))≥1成立,则称f为图G的一个Fractional边全控制函数(简称为F-边全控制函数)。图G的F-边全控制数定义为

并且称满足γ′ft(G)=min{f(E)的F边全控制函数f为一个最小F-边全控制函数。
定义2[7]设G=(V,E)是一个无孤立边的图,如果一个实值函数f:E→[0,1]对任意的e∈E(G)均有f(N(e))≥1成立,则称f为图G的一个F-边全包装函数。图G的一个F-边全包装数定义为
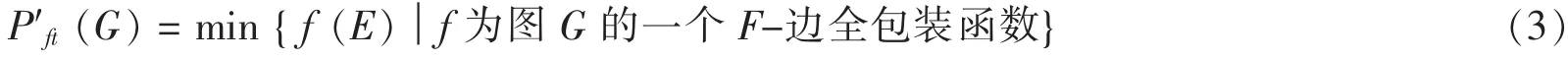
并且称满足P′ft(G)=f(E)的F-边全包装函数f为一个最大F-边全包装函数。
在上述两个定义中,如果将边邻域“N(e)”改为闭边邻域“N[e]”,则对应定义为F-边控制数和F-边包装数。类似地,可分别定义F-点控制函数γ′ft(G)和F-点包装数Pf(G)。Domke G S[8]等证明了γf(G)=Pft(G)对任意图成立,这表明γ′ft(G)=P′ft(G)对任何无孤立边的图成立。特殊地,如果一个实值函数f:E→[0,1]满足f(N(e))=1对任意e∈E(G)成立,则f为G的一个最小F-边全控制函数,同时f也是图G的一个F-边全包装函数,因此有下面的引理成立。
引理1 设G为一个图,若存在一个实值函数f:E(G)→[0,1],使得对任意的e∈E(G)均有f(N(e))=1成立,则有γ′ft(G)=f(E(G))。
2 主要结果及证明



[1]BONDYJ A,MURTY V S R.Graph Theory with Application[M].Elsevier,Amsterdam,1976.
[2]HAYNES T W,HEDETNIEMI S T,SLATER P J.Domination in Graph[M].Marcel Dekker,Inc New York,1998.
[3]HEDETNIEMI S M,HEDETNIEMI S T,WIMER T V.Linear time resource allocation algorithms for trees.Technical report URI-014,Department of Mathematics[R].Clems on University,1987.
[4]MITCHELL S,HEDETNIEMI S T.Edge domination in trees[J].Congr Numer,1977(19):489-509.
[5]BAOGEN XU.On signed edge domination numbers of graphs[J].Discrete Math,2001(239):179-189.
[6]ARUMUGAM S.Fractional edge domination in graphs[J].APPL ANAL Discrete Math,2009(3):359-370.
[7]徐保根,图的控制与染色理论[M].武汉,华中科技大学出版社,2013.
[8]DOMKE G S,HEDETNIEMI S T,LASKAR R C.Fractional packings,coverings and irredundance in graphs[J].Congr Numer,1988(66):227-238.
Fractional Edge Total Domination Numbers in Graphs
Xu Baogen,Zhao Lixin,Zou Yan
(School of Science,East China Jiaotong University,Nanchang 330013,China)
LetG=(V,E)be a graph without isolated edges,a real functionf:E(G)→[0,1]is said to be a fractional edge total domination function(FETDF)of G ifholds for everye∈E(G)edge,then the fractional edge total domination number酌ft′(G)ofGis defined asis a FETDF of G}.This paper determines bounds for the fractional edge total domination numbers of a graph.Meanwhile,it discusses some questions on the fractional edge total domination and gives the fractional edge total domination numbers of some special graphs.
fractional edge total dominating function;fractional edge total domination number;fractional edge total packing function;fractional edge total packing number
O157.5
A
1005-0523(2015)06-0106-04
(责任编辑 姜红贵)
2015-05-03
国家自然科学基金项目(11361024);江西省高校科技落地计划项目(KJLD12067)
徐保根(1963—),男,教授,主要研究方向为图论及其应用。
