基于区分度增量和CPCRLB的传感器管理算法*
2015-12-07徐瑞阳冯新喜孔云波鹿传国
徐瑞阳,冯新喜,孔云波,鹿传国
(1.空军工程大学信息与导航学院,陕西西安710077;2.95806部队,北京100086)
0 引言
目标跟踪是传感器系统的一项重要功能,当使用多只传感器对目标进行跟踪时,由于传感器的能量有限,不能时刻使用所有的传感器进行观测和跟踪,需要根据不同的情况调用传感器资源,同时,传感器与目标的分配管理也是一个至关重要的问题。
Nash M[1]提出使用线性规划确定传感器对目标的分配,使用卡尔曼滤波器中的误差协方差矩阵的迹作为目标函数中的代价系数;Bier SG 和 Rothman P L[2,3]使用布尔矩阵定义了一种以传感器能力和有效性为准的传感器与目标配对方法。童俊和单甘霖[4]提出了一种基于目标跟踪精度Cramér-Rao下限的多传感器跟踪资源协同分配方法。杨小军和马祥[5]提出了一种基于条件后验克拉美—罗下界(CPCRLB)的传感器网络节点管理方法。基于目标信号强度(RSS)推导了目标状态估计均方误差的CPCRLB。利用粒子滤波器逼近目标状态并估计CPCRLB,实现传感器节点在线选择。
本文在上述研究工作的基础上,首先推导了粒子滤波下无源传感器后验CPCRLB的计算公式,然后以目标跟踪后验CPCRLB的相反数作为选择的适应值进行遗传迭代,同时计算目标的区分度增量,通过合理分配传感器资源降低整个跟踪过程中的能耗。
1 传感器分配的一般方法
假定有m只传感器和n个目标,进行传感器管理就是通过分配矩阵将传感器分配给不同的目标,分配矩阵中的元素为0或1,行数为传感器数量,列数为目标数量

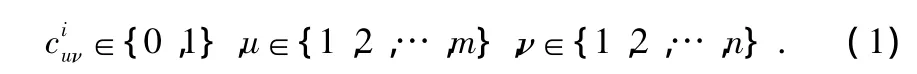
其中,0为该传感器u这一时刻的量测不分配给目标ν,1为传感器u这一时刻的量测分配给目标ν。
以 C={C1,C2,…,C2m×n-1}来表示传感器的分配方案,其中,Ci为不同的传感器分配矩阵,假设每个传感器最多可以跟踪ki(i=1,2,…,n)个目标,设定某种度量方法P(x)作为代价的衡量,所以,传感器管理的模型为

约束条件为
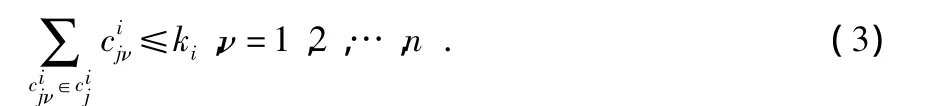
2 粒子滤波下无源传感器的CPCRLB
对一个二维目标进行跟踪,目标的状态方程和量测方程分别为

其中,wk为零均值高斯白噪声,vk为量测噪声并独立于状态噪声wk。
根据文献[5]可得,在k+1时刻对目标状态估计的条件下界满足

其中,L-1(xk+1|z1∶k)为 CPCRLB。
文献[6]提出了一种直接计算CPCRLB的计算方法
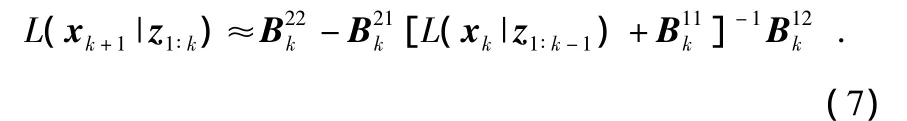
目标跟踪的量测方程为非线性方程

其中,θk=是在无源传感器下,传感器对目标的量测,(ak,bk),(a0,b0)分别为目标位置预测与传感器的横纵坐标。
在加性高斯量测噪声假设下,量测数据的对数似然度为

初始迭代条件为

在式(4)和式(8)确定的状态方程和量测方程下,计算CPCRLB所需的式(8)~式(10)中的数学期望为
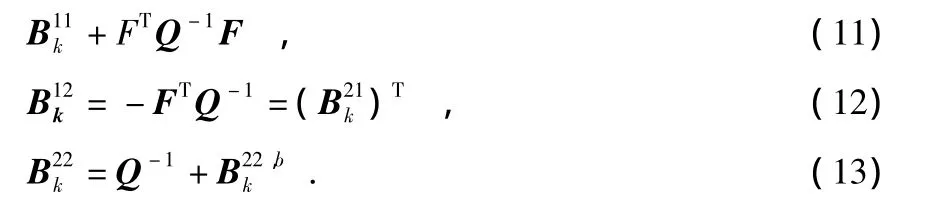
对非线性量测模型,B22,bk通常没有解析表达式。为计算B22,bk,假设目标状态服从一阶Markov过程,采用重要性重采样粒子滤波器进行滤波,重要性函数选为通常使用的状态转移函数,此时权值可由似然函数获得,在重采样后,目标的概率密度函数可近似为

由式(11)~式(14)可得,基于无源量测数据的条件FIM可以迭代逼近计算如下

矩阵B22,bk的元素如下

3 目标区分度增量
当目标之间的距离过近时,需要依据目标之间的区分度制定传感器资源分配策略。根据文献[8],假设k时刻获得的量测为zk,在第k次观测后,目标的区分度由下式计算获得

其中,p(xk|zk)为k时刻获得第k次观测后的后验概率密度函数,第k次观测之后所得的期望区分度增量为

在观测方程为非线性时,需要用采样粒子对结果进行近似,近似后的结果为
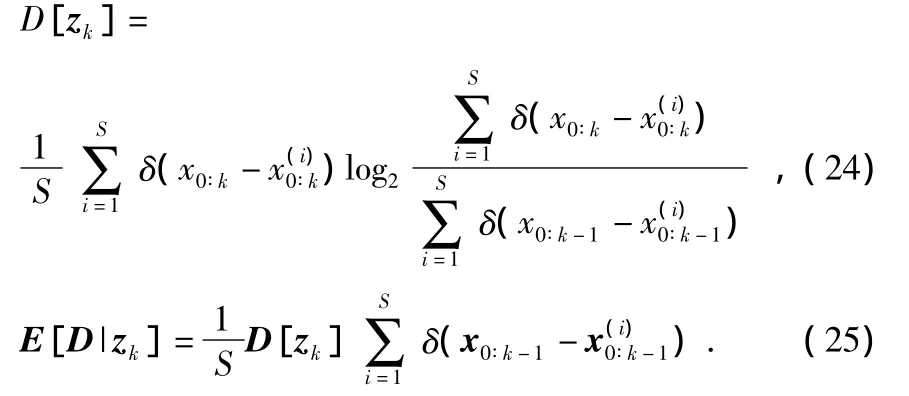
当E[D|zk]小于某个门限值时,就需要调用更多的传感器资源对目标进行更精确的跟踪。
4 算法流程
计算采用矩阵遗传算法作为优化算法,计算每次跟踪的条件后验CPCRLB的相反数作为适应值,并计算每一时刻的目标区分度增量。算法的具体过程如下:
1)随机产生初始的分配矩阵种群,设定交叉和变异概率,设定区分度增量门限值;
2)用初始种群中的个体对目标进行跟踪,计算CPCRLB的相反数作为适应值进行选择,规定分配矩阵中如果有任意一列为全0(该目标没有被跟踪),则适应值为无穷;
3)进行交叉和变异;
4)计算目标的区分度增量;
5)当区分度增量小于设定的门限时,增加传感器的数目;
6)反复进行步骤(1)~(5),根据不同的情况确定不同的传感器分配矩阵对传感器进行分配。
5 仿真与实验结果
设定仿真环境为使用5只传感器对目标进行跟踪,传感器为无源传感器,初始目标为3个,运行传感器数为2只,之后又出现2个目标,目标间距变小。滤波算法采用粒子滤波算法,关联算法采用最近邻算法,选择算子采用轮盘赌算子,种群数量为7个,交叉和变异概率分别设置为pc=0.2,pm=0.3,进行50次蒙特—卡洛仿真。目标航迹和跟踪效果如图1、图2所示。

图1 目标航迹图Fig 1 Target trajectories

图2 跟踪效果图Fig 2 Tracking effect diagram
图1 中从(1,20),(4,30),(6,40)m 起始的三个目标为初始目标;图2中观测站1,2为最初使用的传感器,观测站3,4,5为新目标出现后新调用的传感器,从图2中可以看出:当新出现目标使得目标间距减小时,该算法通过增加传感器数量保证了目标之间的区分和对目标的跟踪。
目标跟踪过程中的区分度增量变化如图3所示。
图3中由于传感器数目带来的跟踪精度影响,目标区分度增量在跟踪初始阶段波动比较大,在20 s时刻新目标出现,目标间距减小导致区分度增量减少,调用更多传感器进行跟踪后,区分度增量逐步增大,并趋于稳定。
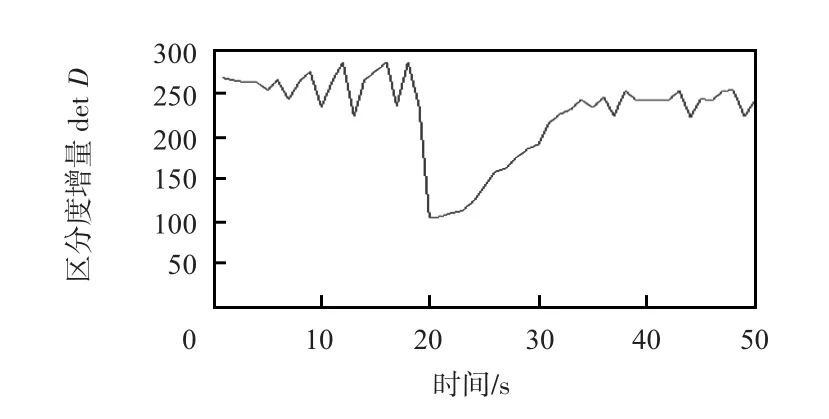
图3 跟踪过程中区分度增量变化情况Fig 3 Change of discrimination gain during tracking process
整个跟踪过程中传感器能量消耗如图4所示。
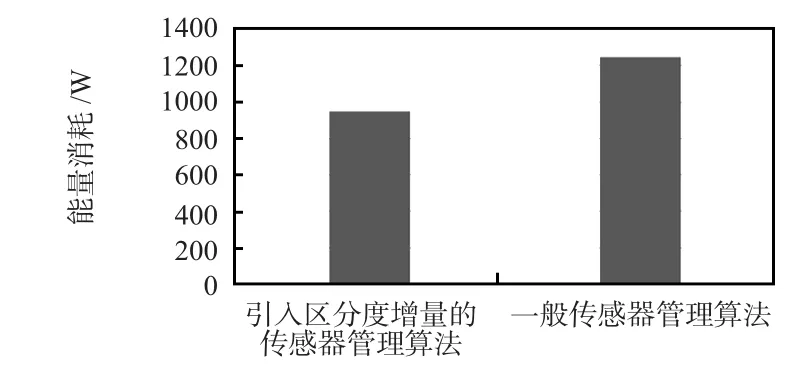
图4 不同算法跟踪过程能量消耗对比Fig 4 Contrast of energy consumption of tracking process of different algorithms
图4显示了引入区分度增量的传感器管理算法和一般传感器管理算法在跟踪过程中能量消耗对比情况,假设传感器在工作时每秒耗能5 W,初始跟踪时只使用了2只传感器对目标进行跟踪,新目标出现后才调用了其他传感器,整个过程中能量消耗950 W,相比于使用全部传感器进行跟踪消耗的1250 W减少了300 W。
跟踪过程中7个个体的适应值变化情况如图5所示。
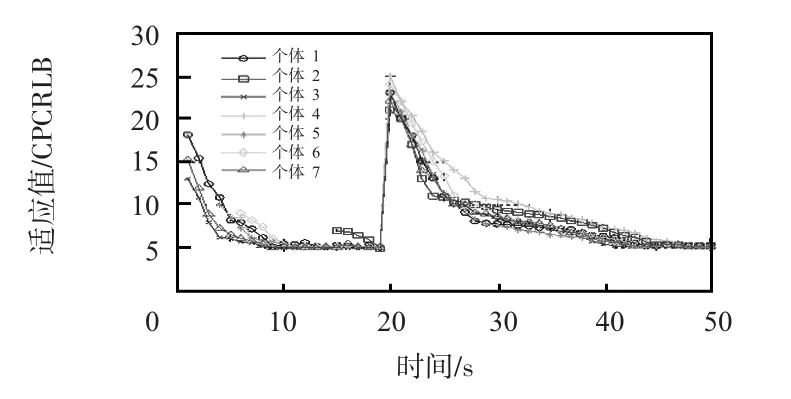
图5 跟踪过程中个体适应值变化情况Fig 5 Change of individual fitness value during tracking process
6 结论
本文基于区分度增量和条件后验CPCRLB提出了一种传感器资源分配算法,这种算法以CPCRLB的相反数作为遗传算法的适应值,同时引入目标区分度增量作为判断目标区分度的标准,相比于用固定数量传感器跟踪目标降低了整个传感器系统的能耗。接下来需要深入研究对异类传感器进行管理和将目标的优先级与算法结合起来。
[1]Nash M.Optimal allocation of tracking resource[C]∥Proceedings of the IEEE Conference on Decision and Control,1977:1177-1180.
[2]Rothman P L,Bier S G.Eva1uation of sensor management systems[C]∥Proceedings of the NAECON,1989:1747-1752.
[3]Bier SG,Rothman P L,Manske R A.Intelligent sensor management for beyond visual range air-to-air combat[C]∥Proceedings of the NAE2CON,1988:264-269.
[4]童 俊,单甘霖.基于Cramér-Rao下限的多传感器跟踪资源协同分配[J].宇航学报,2012,33(9):1314-1321.
[5]杨小军,马 祥,宋青松,等.基于条件后验克拉美—罗下界的目标跟踪传感器管理[J].控制理论与应用,2013,30(5):543-548.
[6]Zuo L,Niu R,Varshney P K.Conditional posterior Cramer-Rao lower bounds for nonlinear sequential Bayesian estimation[J].IEEE Transactions on Signal Processing,2011,59(1):1-14.
[7]Zheng Y,Ozdemir O,Niu R,et al.New conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J].IEEE Transactions on Signal Processing,2012,60(10):5549-5556.
[8]Cai Chenghui,Ferrari Silvia.Comparison of information-theoretic objective functions for decision support in sensor systems[C]∥Proc of the American Control Conference,2007:3559-3564.
[9]李 秉,王凤山.区域防空多传感器管理体系结构与功能模块研究[J].传感器与微系统,2009,28(3):117-120.
[10]张应华,周 林,刘先省.基于测量方差时变的传感器管理算法[J].传感器与微系统,2007,26(3):68-72.
