面向大流量应用的硅微阀致动器优化设计
2015-12-07李勇俊张胜昌
李勇俊,张胜昌,段 飞,邓 宁
(1.清华大学微电子与纳电子学系,北京100084;2.盾安人工环境股份有限公司,浙江杭州310051)
0 引言
微型阀是微流体控制中的关键器件,在生物医疗、工业控制等领域有着重要的应用。常用微型阀种类繁多[1],但处理对象多为细胞,DNA等微流体[2],流量小,压强低,对致动器和微型阀结构的限制相对较小。微型阀的工业应用与医疗、生物领域相比还较少,主要在于传统的微型阀结构难以适应工业生产上高压大流量的应用环境[3,4]。继固体阀、热力阀、电子阀之后,基于MEMS技术的硅微阀流控芯片已成为工业供热通风与空气调节(heating,ventilation and air conditioning,HVAC)领域研究的热点[5]。
本文设计了一种基于V型电热致动器[6,7]的新型硅微阀流控芯片,基于电热耦合理论对该芯片中的V型电热致动器进行优化设计。通过有限元工具Comsol Multiphysics对优化前后的V型电热致动器进行多物理场耦合仿真。结果表明:变截面的优化设计可以在保证致动效果(相同的致动位移)的条件下,改善致动器结构的温度分布,提高致动器的热平衡稳定性和结构稳定性。
1 硅微阀流控芯片的结构
本文设计的硅微阀流控芯片结构如图1(a)所示,该流控芯片由三层硅晶圆键合(wafer bonding)而成,电极口和阀口经各向异性腐蚀(anisotropic etching)形成于第一层和第三层硅片上,第二层为低阻硅材料,芯片结构如图1(b)所示,阵列的V型电热致动器和位移放大结构通过深反应离子刻蚀(deep reactive ion etching)技术一体形成于第二层硅片上。当在V型致动器的两端电极上施加电压后,由于焦耳热效应,阵列的V型梁受热膨胀,在中间直梁上产生初始致动力和致动位移,继而推动位移放大结构,并在位移放大结构末端的微型阀闸门处产生大的输出位移,从而控制阀口处流体的通断,实现对流体的控制作用。

图1 硅微阀流控芯片结构示意图Fig 1 Structure of microfluidic chip of silicon micro-valve
2 基于截面优化的V型电热致动器设计
在V型电热致动器的设计中,应使沿梁的延伸方向上高温区域温度分布更加均匀[8],从而在保障硅微阀流控芯片致动性能的前提下降低V型梁电热致动器的最高温升,提升V型致动器的热平衡稳定性。
国内外对V型电热致动器的优化研究中,变截面设计一直是热点,比较典型的有Shih-Chi ChenAlex等人通过将梁沿长度方向上的设计为两端和中间部位均较窄的轮廓以获得优良的致动器的动态性能[9];Anthony G Fowler等人通过假定V型梁的宽度随梁长度变化关系以提高致动器的灵敏度、线性度和噪声特性[10];而Alex Man Ho Kwan等人通过设计不一致的长度、宽度、倾斜角度的阵列型V型梁来改善致动器的致动性能[11]。但是,上述研究均局限在V型梁厚度非常小(2μm)的情况下,对V型梁在硅微阀流控芯片中的应用缺乏可参照性,并且在衡量优化设计后的致动效果时,上述研究中没有考虑到V型梁致动器阻值对致动性能的影响,影响结果的可信度。
3 设计方法与模型构建
鉴于V型电热致动器两端电极区域温度与环境温度相同,而中间结合处温度最高,为了获得在最高温度附近更趋均匀的温度分布,最好将温度分布模型构建为台阶型而非抛物线型,如图2所示,取环境温度为T0(单位为K),V型梁沿梁方向的总长度为L(单位为m),沿梁方向的位移为x(单位为m),设电极区域温度和周围环境温度相同,则有T(0)=T(L)=T∞=T0,而阵列V型梁中间结合处的温度最高,则有 T(L/2)=Tmax,且有 ΔTm=T(L/2)-T0。

图2 V型电热致动器结构简图Fig 2 Structure of V-shape electro-thermal actuator
故本文利用双曲正切函数构建的V型梁温度沿梁长度方向的分布优化模型可表示为
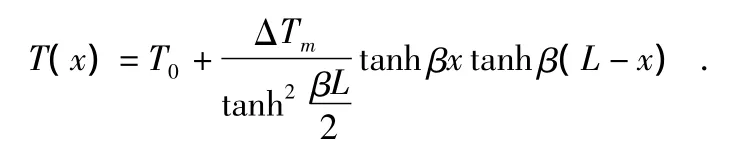
其中,β是与温度分布均匀程度有关的待定系数,m-1。
模型设计时仅考虑V型梁工作的理想情况,则V型梁电热致动器的热生成率(steady-state heat-generation rate)为,由于焦耳热效应,则V型梁电热致动器上的电流密度为,故有
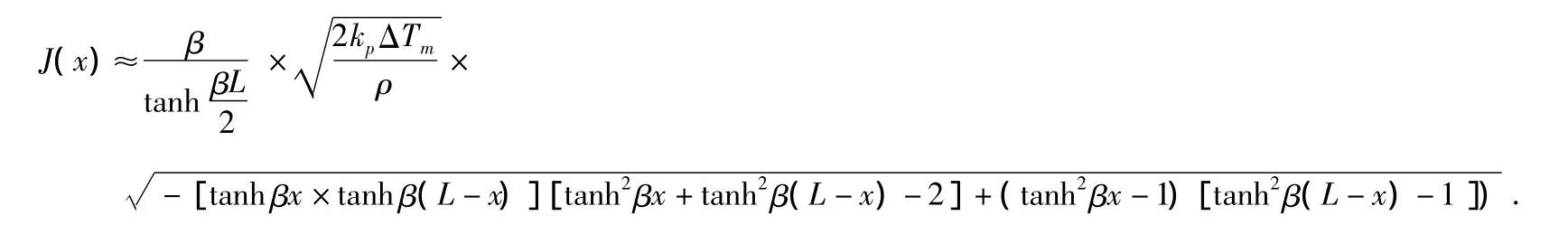
根据电流I=J(x)w(x)t得,截面宽度w(x)沿V型梁 电热致动器长度方向的分布为(其中,t为致动器的厚度,m)

实际上,对于同一V型梁上的各截面,I为定值,ΔTm为设计所需的温升极限,L是V型梁的整体长度,由实际芯片尺寸决定,则截面宽度只与β值与该截面在梁延伸方向上离电极区域的距离x有关。
在硅微阀流控芯片中,取最高温升上限为 ΔTm=700 K,取L为5000μm,厚度t为400μm。由于实际过程中电流I为定值,取为0.8 A,得到不同β值对应的温度、电流密度的变化曲线如图3所示(图例取1/β的数值)。
随着β值的增大,温度分布由“抛物线”型向“台阶型”转化,超过一定范围后,V型梁中间截面内的电流密度过小,导致截面宽度急剧变化,不适合实际的设计。本文取折衷状态下的β值(β=1/(1000μm))以获得变截面V型致动器的宽度分布,进而得到优化后的V型致动器模型,再由欧姆定律得到与其等阻值的恒定截面V型致动器的宽度,构建优化前的参考模型。
4 结果与讨论
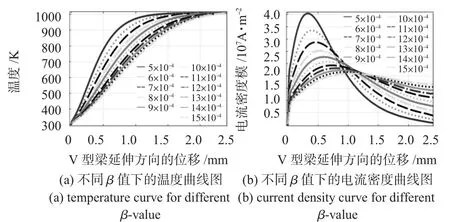
图3 不同β值下的温度和电流密度曲线图Fig 3 Temperature and current density curve for differentβ-value
硅微阀流控芯片工作在流体环境中,在致动器的电极上施加电压后,由于焦耳热效应,致动器由于受热膨胀而产生致动位移,是热—电—结构—流体全耦合过程,采用适当的设计,可以将硅微阀流控芯片设计为压力平衡的形式,在仿真过程中可忽略流体对致动器的阻力作用,在运用Comsol Multiphysics进行仿真时,采用热—电—结构耦合模型,并考虑致动器与周围流体的传导、对流和热辐射效应,可以有效模拟出致动器在流体场中的工作过程[12]。
如图4所示,当在电极上施加电压为8.8 V时,恒定截面梁的最高温升达到温升上限ΔTm=700 K,如图4(a),此时阵列V型梁的致动最大位移位于中间结合处的直梁上,为18.48μm,而图4(b)表示当等阻值的变截面V型梁(Non-uniform actuator)的致动位移达到与恒定截面V型梁(uniform actuator)的最大位移一致时的情况,此时变截面V型梁的最大位移也位于中间直梁上。
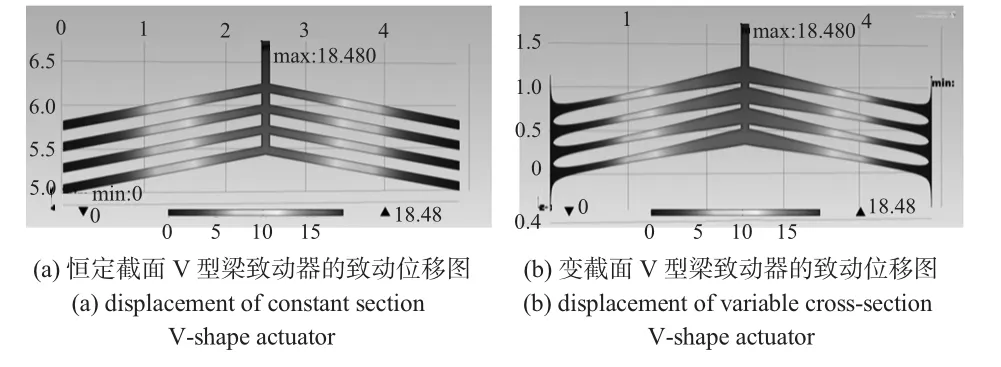
图4 恒定截面与变截面V型致动器的致动位移图Fig 4 Actuating displacement of constant section and variable cross-section V-shape actuator
当致动位移相同时,恒定截面V型梁和变截面V型梁的温度分布如图5所示,表明变截面V型梁中心轴线上的温度分布呈“台阶型”,而恒定截面V型梁呈“抛物线”型,优化后的V型梁的高温段更平缓且高温区域更宽,相比恒定截面V型梁更难达到温升的上限值,而优化后的V型梁的低温段与恒定截面梁的低温段相比低温区域更窄且曲线斜率更大,对V型梁的热膨胀影响相对更小。在达到恒定截面梁的最大位移时,恒定截面梁的温度达到温升上限值ΔTm=700K,而变截面梁的此时梁上的最高温升为650 K,即在获得相同致动位移的前提下,变截面梁比恒定截面梁的最高温升下降7.14%。

图5 恒定截面与变截面V型致动器位移相同时的温度分布图Fig 5 Temperature distribution of constant section and variable section V-shape actuators for same displacement
图6显示的是达到相同致动位移时恒定截面梁和变截面梁的应力分布情况,由图6(a)可知,恒定截面梁的最大应力出现在梁与电极的连接处,而变截面梁的最大应力比恒定截面梁更小;由图6(b)可知,变截面梁的应力分布比恒定截面梁的应力分布更为均匀,不会出现恒定截面梁在与电极连接处的应力集中现象,故优化后的应力分布更为均匀,结构稳定性更好。

图6 恒定截面与变截面V型致动器位移相同时的应力图Fig 6 Stress distribution of constant section and variable section V-shape actuators for same displacement
5 结论
本文设计了一种基于变截面V型电热致动器的硅微阀。结果表明:采用温度分布优化模型构建的变截面V型梁高温区域温度分布更均匀,且在未达到极限温升时即可达到恒定截面V型梁的极限致动位移,在致动位移相同的情况下可以降低硅微阀流控芯片内部的最高温度,改善硅微阀流控芯片内部的热平衡稳定性。优化后的V型致动器应力变化也更平缓,消除了在梁与电极接触区域的应力集中现象,提升了V型梁电热致动器的结构稳定性。采用温度分布优化模型构建的V型致动器在保障致动性能的情况下明显提高了致动器的稳定性和可靠性。
[1]Oh K W,Ahn CH.A review of microvalves[J].Journal of Micromechanics and Microengineering,2006,16(5):13-39.
[2]Hesketh P J,Bintoro J S,Luharuka R.Microvalve for fuel cells and miniature gas chromatographic system[J].Sensors Update,2003,13(1):233-302.
[3]Williams K R,Maluf N I,Fuller E N,et al.A silicon microvalve for the proportional control of fluids[C]∥The 10th International Conference on Solid-State Sensors and Actuators,Transducers’99,Sendai,Japan,1999:1804-1807.
[4]Haasl S,Braun S,Ridgeway A S,et al.Out-of-plane knife-gate microvalves for controlling large gas flows[J].Journal of Microelectromechanical Systems,2006,15(5):1281-1288.
[5]Allan R.MEMSsilicon expansion valve heads toward new HVAC applications[J].Electronic Design,2010,58(16):78.
[6]Que L,Park J S,Gianchandani Y B.Bent-beam electrothermal actuators—Part I:Single beam and cascaded devices[J].Journal of Microelectromechanical Systems,2001,10(2):247-254.
[7]Park J S,Chu L L,Oliver A D,et al.Bent-beam electrothermal actuators—Part II:Linear and rotary microengines[J].Journal of Microelectromechanical Systems,2001,10(2):255-262.
[8]Sassen W P,Henneken V A,Tichem M,et al.Contoured thermal V-beam actuator with improved temperature uniformity[J].Sensors and Actuators A:Physical,2008,144(2):341-347.
[9]Chen SC,Culpepper M L.Design of contoured thermomechanical actuators and pulsing actuation to enhance dynamic performance[J].Journal of Microelectromechanical Systems, 2012,21(2):340-349.
[10]Bazaei A,Fowler A G,Moheimani SOR.Improved electrothermal position sensing in MEMS with non-uniformly shaped heaters[C]∥The 11th IEEE Conference on Sensors,Sensors2012,Taipei,Taiwan:IEEE,2012:1-4.
[11]Kwan A M H,Song S,Lu X,et al.Improved designs for an electrothermal in-plane microactuator[J].Journal of Microelectromechanical Systems,2012,21(3):586-595.
[12]Hickey R,Kujath M,Hubbard T.Heat transfer analysis and optimization of two-beam microelectromechanical thermal actuators[J].Journal of Vacuum Science & Technology A,2002,20(3):971-974.
