悬挑十字交叉基础梁节点荷载分配方法探讨

林丽萍，罗 婉，贺建清

（湖南科技大学 土木工程学院，湖南 湘潭 411201）

悬挑十字交叉基础梁节点荷载分配方法探讨

林丽萍，罗 婉，贺建清

（湖南科技大学 土木工程学院，湖南 湘潭 411201）

将半无限长梁自由端无限延伸，形成无限长梁；基于Winkler地基上无限长梁的解答，求得集中力偶作用下原半无限长梁自由端处的剪力和弯矩。利用半无限长梁自由端需满足弯矩及剪力为零的条件，求得需在自由端施加的外荷载。分别计算外荷载和集中力偶在作用点处产生的挠度，叠加求得集中力偶作用下半无限长梁在作用点处的挠度，并提出集中力偶作用下的悬挑影响系数计算公式。根据静力平衡和变形协调条件，建立竖向荷载和力矩共同作用下具有悬挑的十字交叉基础的节点分配荷载的一般公式。

Winkler地基；十字交叉基础梁；半无限长梁；节点；荷载分配

1 研究背景

对于荷载较大的高层建筑，如果地基软弱，且土的压缩性或柱荷载沿两个柱列方向不均匀，需要基础纵横两向都有一定的抗弯刚度，以减少地基变形，防止过大的不均匀沉降时，常采用双向设置的十字交叉基础[1-4]。此种基础刚度较大，能有效地减小柱基之间的沉降差，从而满足地基承载力和地基变形的要求，以保证建筑物的可靠性[5]。

十字交叉基础是由柱网下的纵、横相连的条形基础组成的一种空间体系，其与地基相互作用的理论分析相当复杂。目前，因考虑上部结构-基础-地基共同作用的分析方法尚不成熟，工程上常采用一些近似计算方法来解决节点处柱荷载的分配问题。文献[6]给出了Winkler地基上十字交叉基础梁包含有限长梁及节点不在梁端的半无限长梁的节点分配荷载的一般公式。文献[7]基于无限长Winkler地基梁的解答，推导出具有悬挑的十字交叉基础梁柱荷载分配系数的公式。文献[8]给出了合理的重叠基底反力调整方法及计算公式，并通过算例对节点力调整前后基底反力及内力的变化进行了对比。文献[9]提出了一种计算位于双参数地基模型上，具有悬挑的十字交叉基础梁柱荷载分配系数的方法。文献[10]建立了满足地基承载能力要求的基础底板宽度的计算公式。文献[11]提出了空间框架-十字交叉基础梁与弹性地基相互作用简化分析的超元法。文献[12]提出了弹性地基上十字交叉梁考虑上部结构影响分析的超元法。以上研究在对节点处荷载进行分配时，考虑了地基与基础的共同作用，且满足静力平衡和变形协调2个条件，但均忽略了上部结构传来的力矩对节点位移的影响；文献[13]中虽有提及，但没有给出考虑力矩影响的节点荷载简化分配方法。

在工程实际中，为调整结构荷载中心与基底平面形心相重合和改善角柱与边柱下地基受力条件，常在转角和边柱处，基础做构造性延伸。本文基于Winkler地基上无限长梁的解答，推导出集中力偶作用下半无限长梁在作用点处挠度，提出了集中力偶作用下的悬挑影响系数计算公式；根据静力平衡和变形协调条件，建立竖向荷载和力矩共同作用下具有悬挑的十字交叉基础的节点分配荷载一般公式。

2 Winkler地基上梁节点荷载分配计算

2.1 Winkler地基上梁挠曲微分方程

Winkler地基上梁的荷载分配分析见图1。图中：x为到远点的距离；p为基底反力，p(x) 为点x处的基底反力；q为分布荷载，q(x)为点x处的分布荷载；M为弯矩；V为剪力。

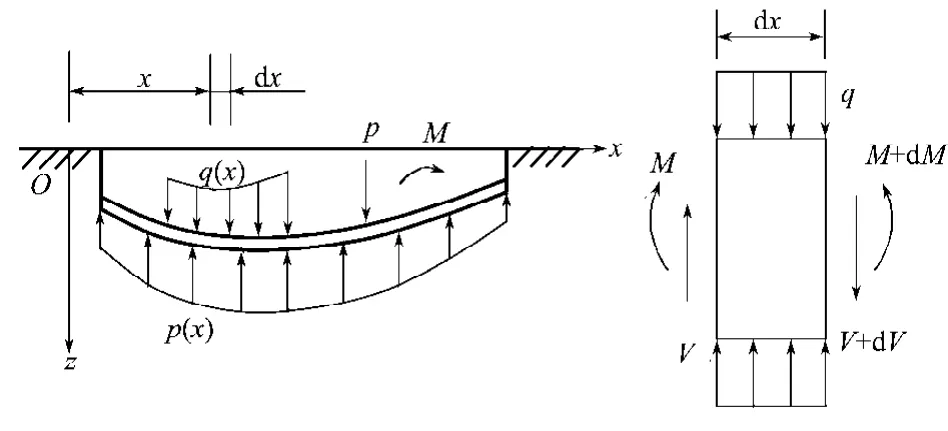
图1 Winkler地基上节点荷载分配分析简图Fig.1 Sketch of load distribution of joint on Winkler foundation

Winkler地基上梁挠曲微分方程为[14-15]

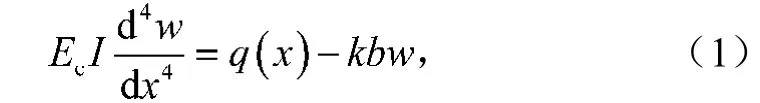
式中：Ec, I分别为基础梁的弹性模量和惯性矩；

k为地基抗力系数；

b为基础梁的宽度；

w为梁的挠度。

2.2 Winkler地基上无限长梁的节点荷载分配

在Winkler地基上的无限长梁上分别施加一集中力P、集中力偶M0，从而得无限长梁的挠度w、转角 、弯矩M及剪力V，见图2[16]。图中，为弹性地基梁的特征系数，Ax, Bx, Cx, Dx均为参数，且

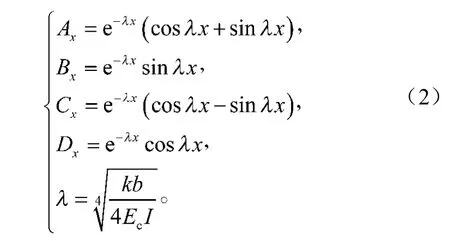
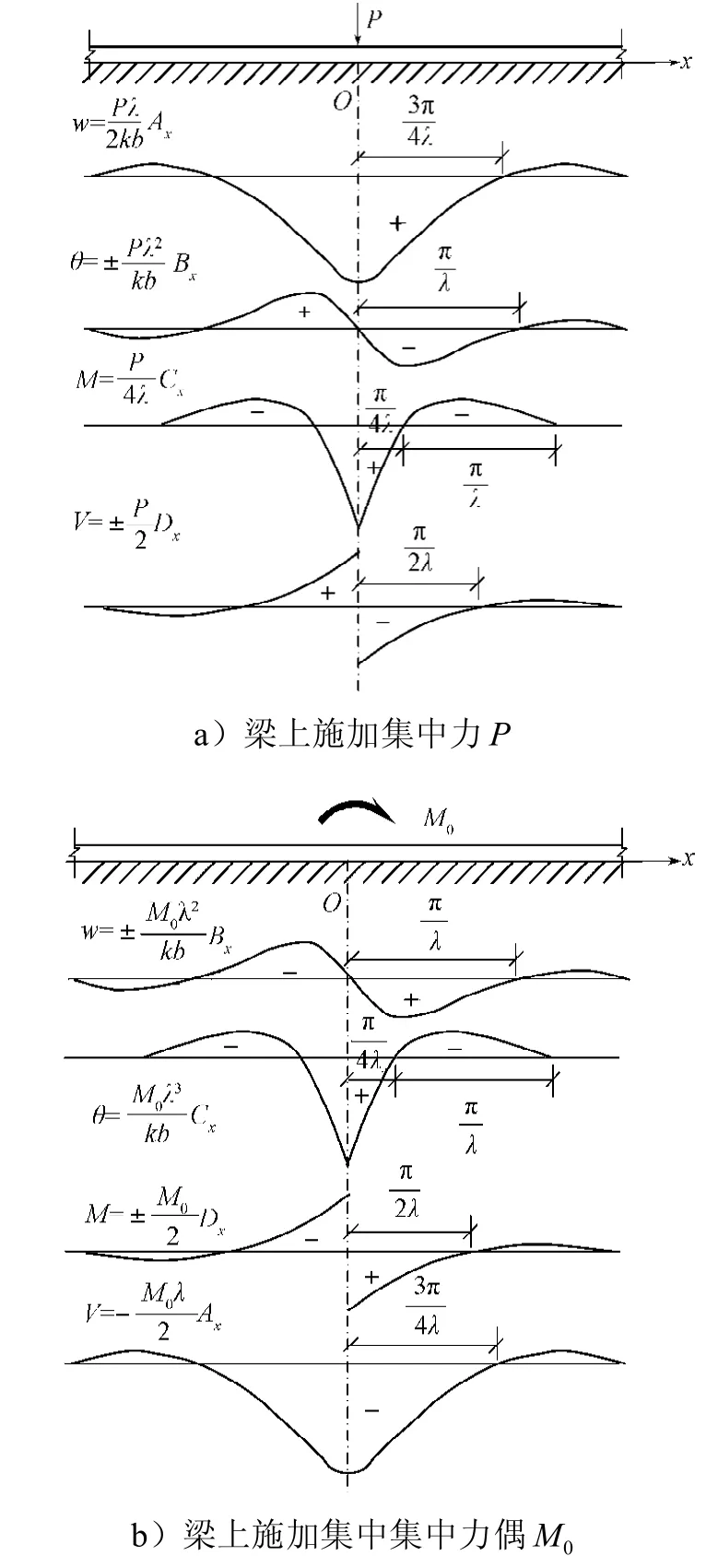
图2 Winkler地基上无限长梁的挠曲和内力Fig.2 Deflection and inner force of infinite beam on Winkler foundation

2.3 Winkler地基上半无限长梁集中力作用点处挠度

如图3所示，在半无限长梁上作用集中力P0，作用点O距梁端A的距离为，则作用点O处梁的挠度[7]

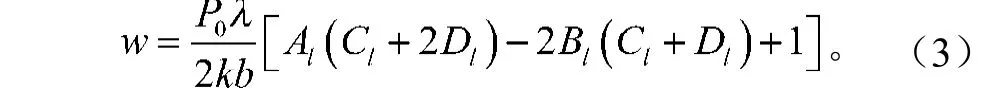
令

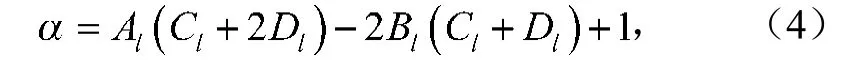
从而得

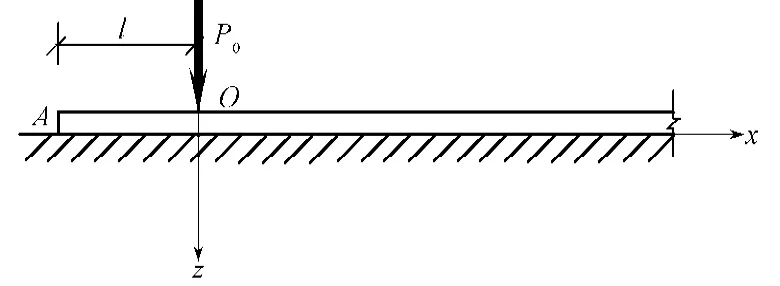
图3 集中力作用下的半无限长梁Fig.3 Semi-infinite beam under concentrated force

图4 为集中力作用下悬挑影响系数曲线。

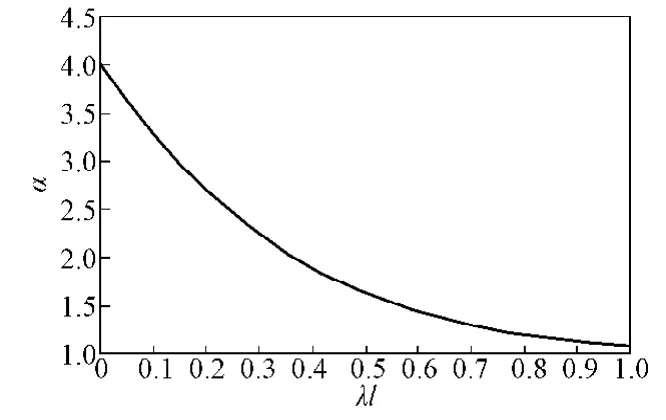
图4 集中力作用下的悬挑影响系数曲线Fig.4 Cantilever-influence coefficient curve under concentrated force

2.4 Winkler地基上半无限长梁集中力偶作用点处的挠度

如图5所示，在半无限长梁上施加集中力偶M0，作用点O距梁端A的距离为利用叠加原理求解作用点O处梁的挠度，求解方法如下：

将梁从A端向外无限延伸形成无限长梁，按无限长梁方法求解力偶M0在A截面产生的弯矩Ma、剪力Va。由于原半无限长梁A端为自由端，弯矩及剪力均为0，故在无限长梁A处加上弯矩MA、剪力VA以抵消M0在无限长梁上A处产生的弯矩Ma、剪力Va，满足自由端弯矩及剪力为0的条件。求得弯矩MA、剪力VA后，分别求力偶M0、弯矩MA、剪力VA在无限长梁O处的挠度，然后叠加求出O处的挠度。

求解步骤如下：

1）根据图2b中公式，力偶M0在无限长梁A截面产生的弯矩Ma、剪力Va为

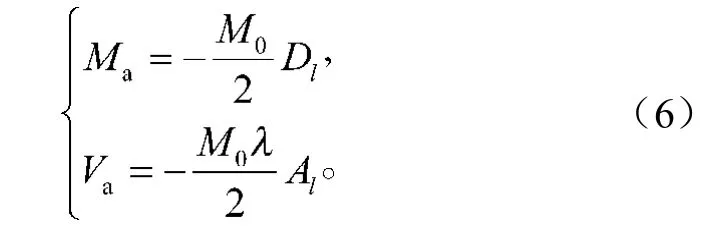
2）根据在无限长梁A处施加的弯矩MA、剪力VA，在该处产生的弯矩、剪力分别为-Ma,-Va的条件，由图2中公式，建立如下方程：

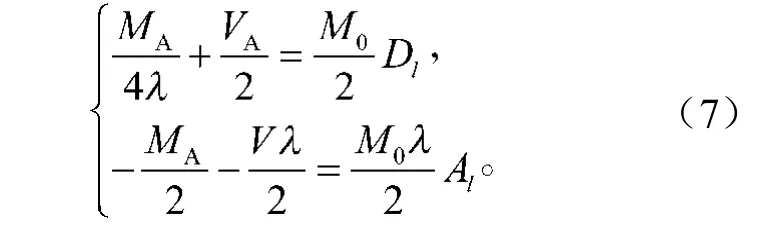
求解方程（7）得

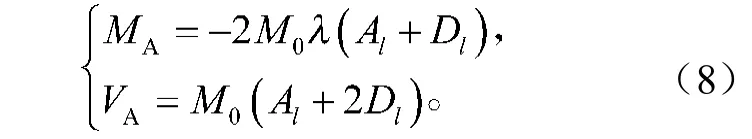
3）由图2中公式分别求得力偶M0、弯矩MA、剪力VA在无限长梁O处的挠度，叠加得

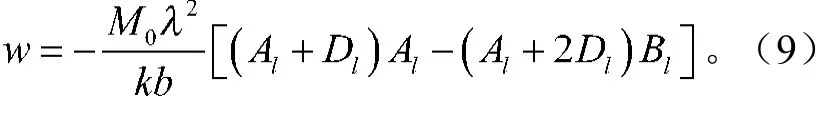
令

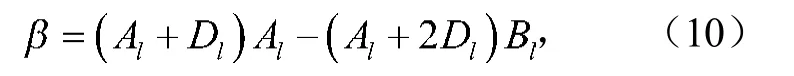
从而得

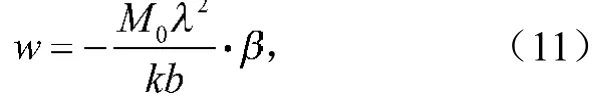
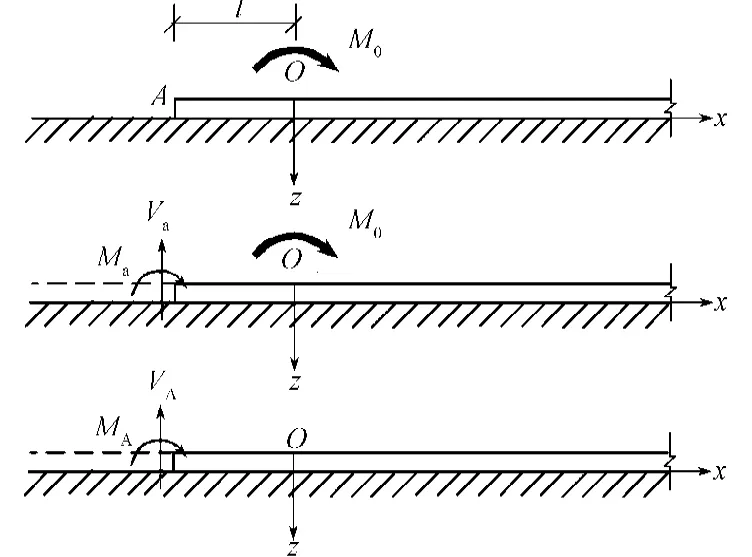
图5 集中力偶作用下的半无限长梁内力和挠度计算Fig.5 Calculation of deflection and inner force of semi-infinite beam under concentrated couples

图6 为集中力偶作用下悬挑影响系数曲线。

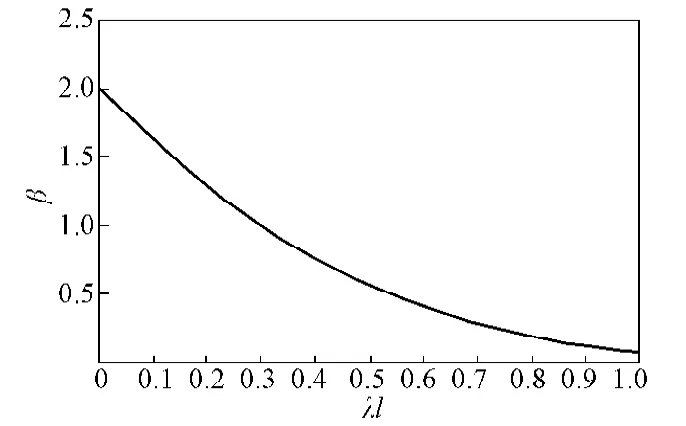
图6 集中力偶作用下的悬挑影响系数曲线Fig.6 Cantilever-influence coefficient curve under concentrated couples

3 十字交叉基础节点荷载分配

在如图7所示的十字交叉基础简图上，任一交叉点处都作用有从上部结构传来的竖向荷载Fi和x,y方向的力矩Mix, Miy。不考虑扭转变形的影响，即一个方向的条形基础有转角时，不引起另一方向条形基础的内力，Mix, Miy分别由x, y方向基础承担[17]。

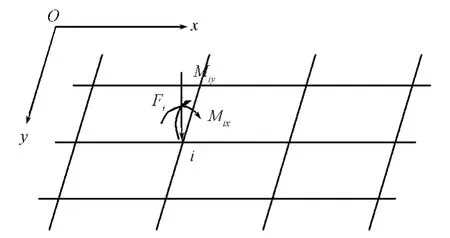
图7 十字交叉基础简图Fig.7 Sketch of crossed foundation beams

考虑基础与地基的共同作用，对任一节点，荷载分配必须满足以下2个条件：

1）静力平衡条件。节点处分配在x, y方向条形基础的竖向荷载之和等于柱荷载，即

式中：Fi为任一节点上作用的柱荷载；

Fix, Fiy分别为分配在x, y方向条形基础梁上的竖向荷载。

2）变形协调条件。即x, y方向条形基础梁在节点处的挠度相等。

式中，wix,wiy分别为x, y方向条形基础梁在节点处的挠度。

文献[13]在分配十字交叉基础节点荷载时，把交叉基础分成6种不同的类型，本文采用文献[7]的分类方法，统一把节点分成3类：内柱节点，见图8a；边柱节点，见图8b；角柱节点，见图8c。

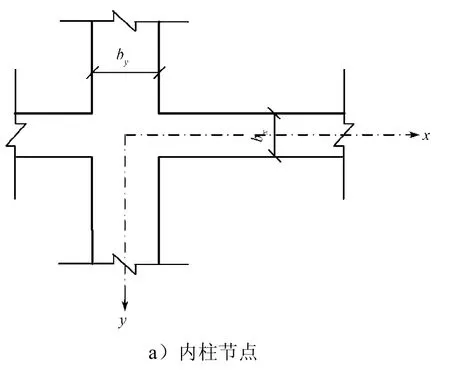
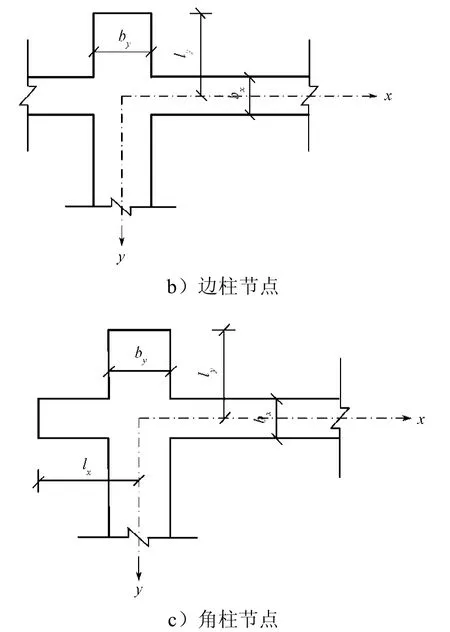
图8 交叉基础节点类型Fig.8 Various joints of crossed foundation beams

3.1 内柱节点荷载分配

对内柱节点（图8a所示），Fix, Fiy分别为柱荷载Fi分配在x, y方向条形基础梁上的竖向荷载。根据Winkler地基上无限长梁的解，x方向条形基础梁在Fix作用下，i节点产生的挠度为

式中：bx为x方向基础宽度；

Sx为x方向基础的弹性特征长度，

同理，y方向条形基础梁在Fiy作用下，i节点产生的挠度为

式中：by为y方向基础宽度；

Sy为y方向基础的弹性特征长度，

由式（12）～（15）解得

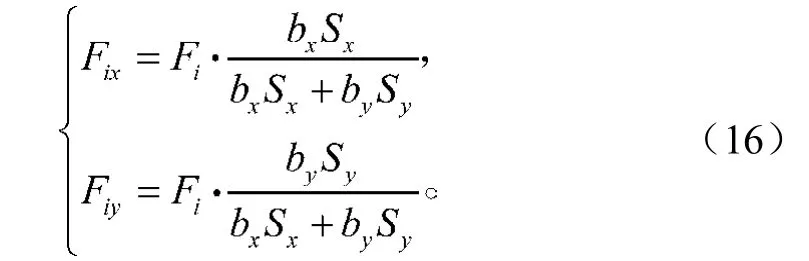
3.2 边柱节点荷载分配

对边柱节点（图8b所示），节点柱荷载Fi可分解为作用在无限长梁上的Fix和作用在半无限长梁上的Fiy。由式（5）和式（11）可知，y方向条形基础梁在Fiy, Miy作用下，i节点产生的挠度为

3.3 角柱节点荷载分配

对角柱节点（图8c所示），节点柱荷载Fi可分解为分别作用在半无限长梁上的竖向荷载。同3.2节类似，x方向条形基础梁在Fix, Mix作用下，i节点产生的挠度为

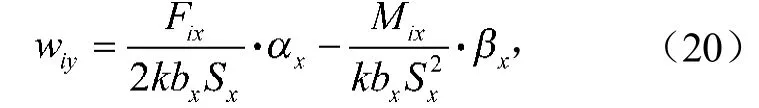
由式（12）～（13）和式（17）～（18）解得

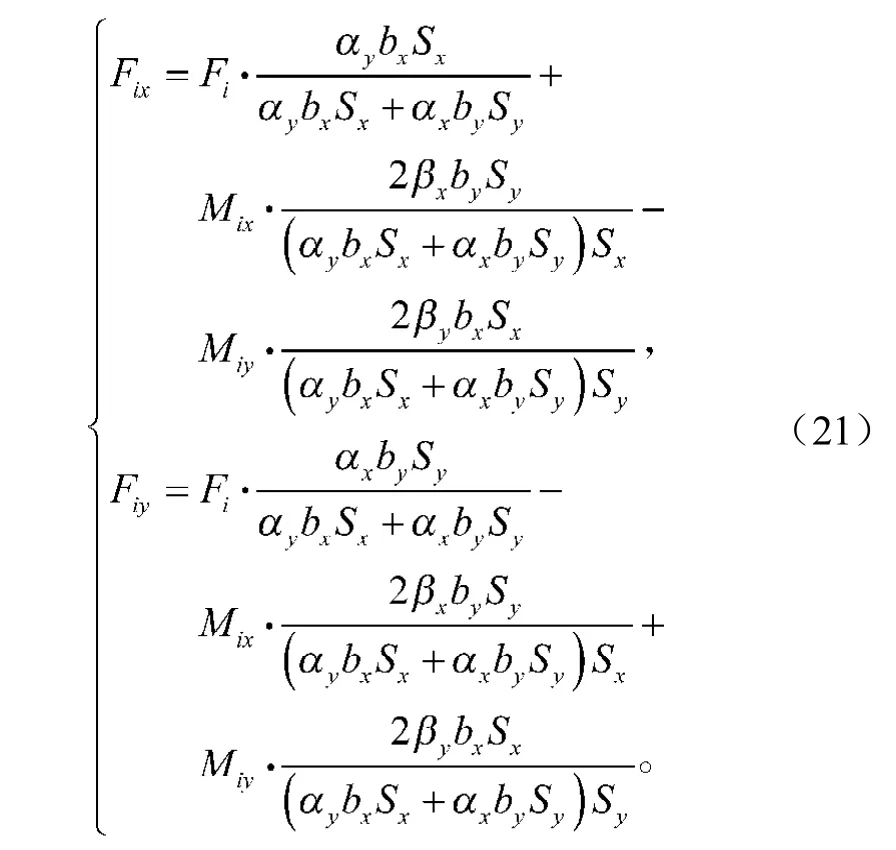
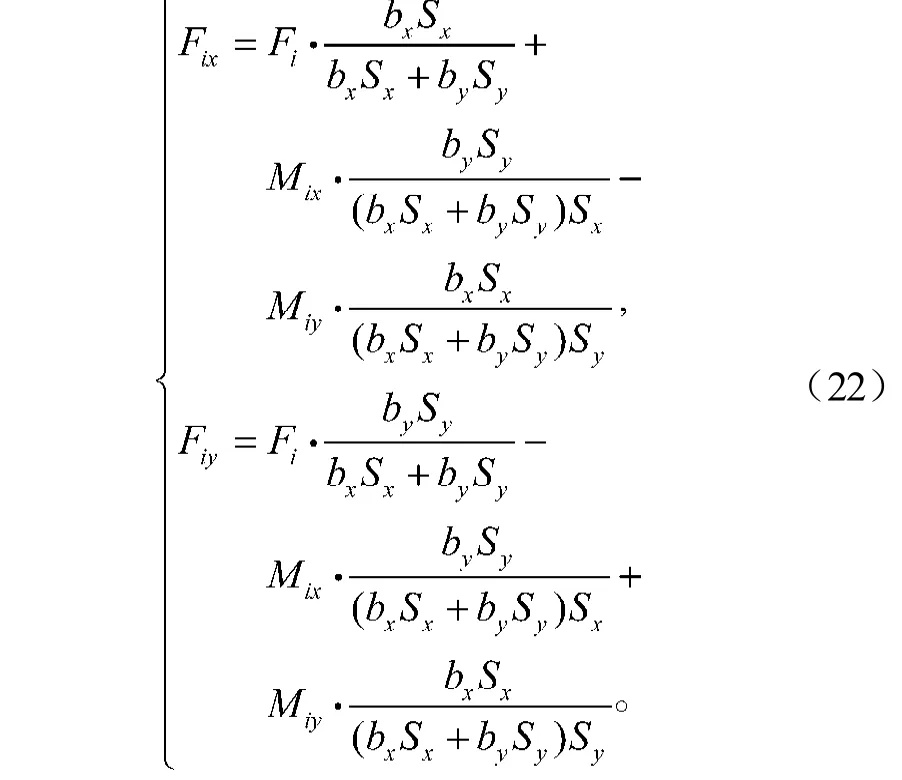
在将节点上的柱荷载进行分配的过程中，基底面积重复计算一次，使基底单位面积上的反力较实际的反力减少，计算结果偏于不安全，必须进行调整修正。经调整后，i节点x, y方向基础梁上的荷载为[16]

式中：ΔAi为i节点多算了的基底面积；

p为调整前的基底压力平均计算值。

4 算例

本文选取文献[12]中算例，图9为某框架结构基础平面。

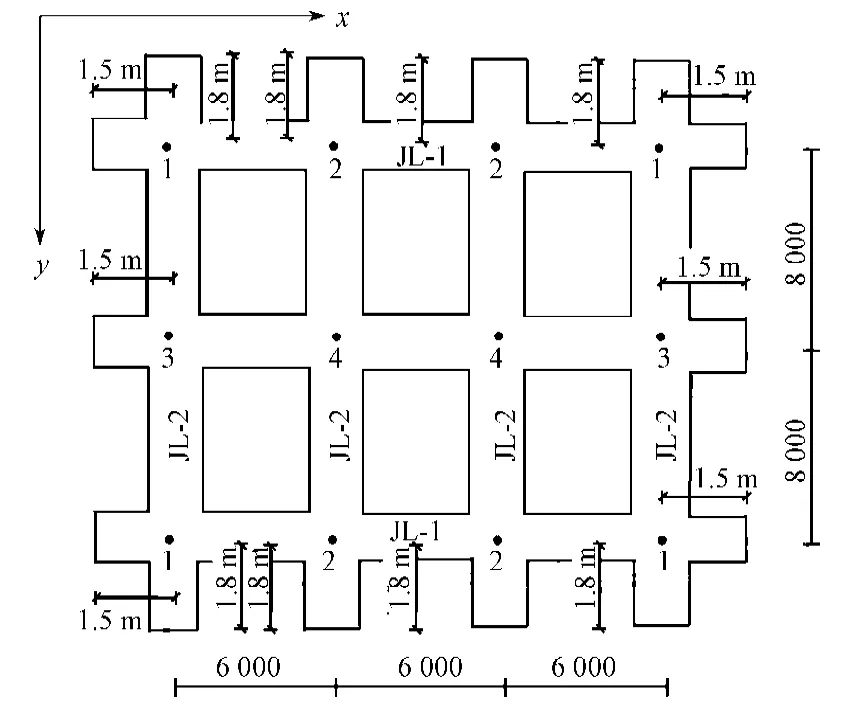
图9 计算实例Fig.9 The calculation example

已知柱荷载F1=2 400 kN，F2=3 200 kN，F3=4 000 kN，F4=4 500 kN；弯矩M1x=30.0 kN·m，M1y=33.8 kN·m，M2x=23.8 kN·m，M2y=28.0 kN·m，M3x=35 kN·m，M3y=33.0 kN·m，M4x=26.3 kN·m，M4y=28.0 kN·m。持力层地基抗力系数k=5×104kN/m3，基础混凝土弹性模量Ec=2.55×107kN/m2，x方向基础梁的宽度、惯性矩、悬挑长度分别为3.0 m, 0.127 m4, 1.5 m，y方向基础梁的的宽度、惯性矩、悬挑长度分别为2.0 m, 0.110 m4, 1.8 m。

4.1 节点荷载分配

对JL-1基础梁，有bx=3.0 m，Ix=0.127 m4，

对JL-2基础梁，有by=2.0 m，Iy=0.110 m4，

采用式（16）、式（18）和式（21）分别计算分配在x, y方向条形基础梁上的竖向荷载Fix, Fiy，计算结果见表1。

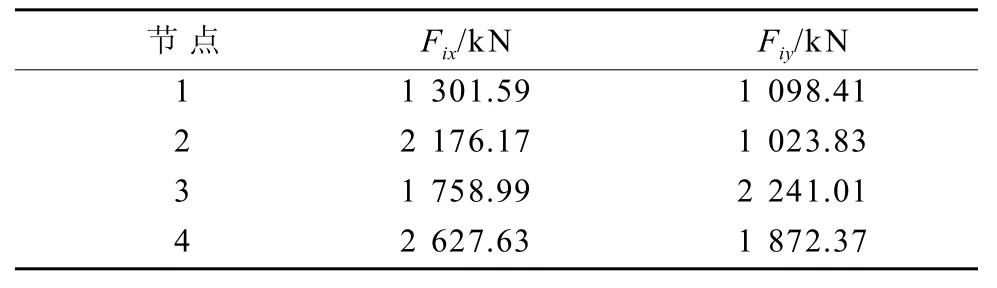
表1 节点竖向荷载分配Table 1 Distribution of vertical load on joints

4.2 分配荷载调整

作用在诸节点上集中力的总和为

基础的实际底面积为

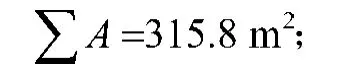
交叉基础各节点重叠的基地面积之和为

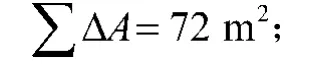
调整前的基底压力平均计算值为

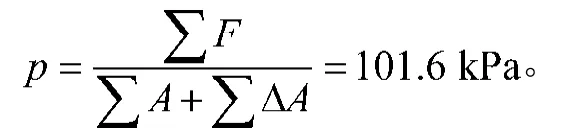
由式（16）可得各节点经调整后的分配荷载。计算结果见表2。

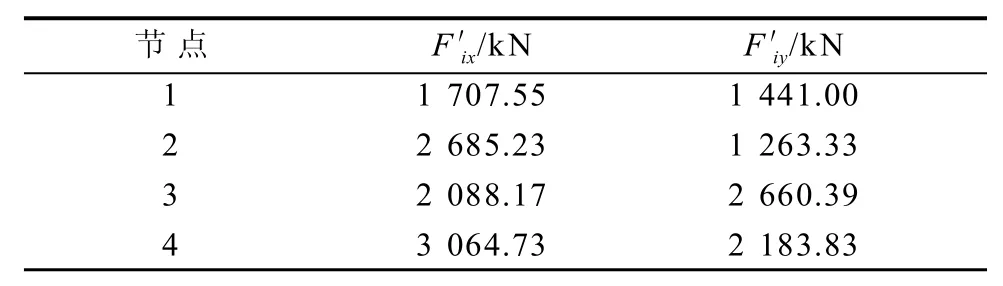
表2 节点分配荷载调整Table 2 Adjustment of distributed loads on joints

5 结语

1）基于对Winkler地基上无限长梁的解答，推导出集中力偶作用下半无限长梁在作用点处的挠度，提出了集中力偶作用下的悬挑影响系数的计算公式。

2）根据静力平衡和变形协调条件，建立了竖向荷载和力矩共同作用下十字交叉基础的边柱和角柱节点分配荷载的一般公式。

[1] 王 燕，李华军，厉见芬. 半刚性梁柱节点连接的初始刚度和结构内力分析[J]. 工程力学，2003，20(6)：65-69. Wang Yan，Li Huajun，Li Jianfen. Initial Stiffness of Semi-Rigid Beam-to-Column Connections and Structural Internal Force Analysis[J]. Engineering Mechanics，2003，20(6)：65-69.

[2] 叶列平，马千里，缪志伟. 钢筋混凝土框架结构强柱弱梁设计方法的研究[J]. 工程力学，2010，27(12)：102-113. Ye Lieping，Ma Qianli，Miao Zhiwei. Study on Weak Beam-Strong Column Design Method of RC Frame Structures[J]. Engineering Mechanics，2010，27(12)：102-113.

[3] 宰金珉，宰金璋. 高层建筑基础分析与设计[M]. 北京：中国建筑工业出版社，1994：154-163. Zai Jinmin，Zai Jinzhang. High-Rise Building Foundation Analysis and Design[M]. Beijing：China Architecture and Building Press，1994：154-163.

[4] Dooley K L，Bracci J M. Seismic Evaluation of Columnto-Beam Strength Ratios in Reinforced Concrete Frames[J]. ACI Structural Journal，2001，98(6)：843-851.

[5] French C W，Moehle J P. Effect of Floor Slab on Behavior of Slab-Beam-Column Connections[J]. ACI Special Publication，1991(123)：225-258.

[6] 李方圆. 十字交叉基础梁的节点荷载分配问题[J]. 西安建筑科技大学学报，1998，30(3)：294-297. Li Fangyuan. Problems on Load Distribution for the Joint of Crossed Foundation Beams[J]. Journal of Xi’an University of Architecture & Technology，1998，30(3)：294-297.

[7] 陈 沙，王贻荪. 十字交叉地基梁柱荷载分配工程实用统一算法[J]. 勘察科学技术，1999(4)：42-46，54. Chen Sha，Wang Yisun. Practical Unified Algorithm in Construction for Distribution of Column Load on Crossed Foundation Beam[J]. Site Investigation Science and Technology，1999(4)：42-46，54.

[8] 秦植海，李根生，张维圈. 柱下钢筋混凝土十字交叉基础节点力的分配[J]. 力学与实践，1999，21(5)：22-24. Qin Zhihai，Li Gensheng，Zhang Weiquan. PressureDistribution at Nodal Point of Reinforced Concrete Crossed Foundation Under Column[J]. Mechanics and Engineering，1999，21(5)：22-24.

[9] 邱 畅，王贻荪. 基于双参数地基模型的十字交叉梁柱荷载分配系数工程实用算法[J]. 勘察科学技术，2000(5)：22-27. Qiu Chang，Wang Yisun. The Engineering Practical Calculation Method of Criss-Cross Beam and Column Load Distribution Coefficient Based on Double-Parameter Foundation Model[J]. Site Investigation Science and Technology，2000(5)：22-27.

[10]王 龙，朱彦鹏，李庆福. 十字交叉梁基础合理基础底板宽度的计算方法[J]. 甘肃工业大学学报，2002，28(3)：98-100. Wang Long，Zhu Yanpeng，Li Qingfu. Calculation Method for Reasonable Width of Baseplate of Grillage Foundation [J]. Journal of Gansu University of Technology，2002，28(3)：98-100.

[11]孙建琴，刘 勇，李从林. 空间框架-十字交叉基础梁与弹性地基相互作用简化分析的超元法[J]. 岩土工程学报，2003，25(2)：225-227. Sun Jianqin，Liu Yong，Li Conglin. Super Element Method for Analyzing Interaction of Space Frame-Grillage Foundation Beams on Elastic Foundation[J]. Chinese Journal of Geotechnical Engineering，2003，25(2)：225-227.

[12]孙建琴，李从林，刘 勇. 弹性地基上十字交叉梁考虑上部结构影响分析的超元法[J]. 土木工程学报，2004，37(2)：28-32. Sun Jianqin，Li Conglin，Liu Yong. Super Element Method for Analyzing Grillage Beams on Elastic Foundation Considering Influence of Upper Structures[J]. China Civil Engineering Journal，2004，37(2)：28-32.

[13]张季容，朱向荣. 简明建筑基础计算与设计手册[M]. 北京：中国建筑工业出版社，1997：53-60. Zhang Jirong, Zhu Xiangrong. Concise Manual of Buildings Foundation Calculation and Design[M]. Beijing：China Architecture and Building Press，1997：53-60.

[14]Selvadurai A P S. Elastic Analysis of Soil-Foundation Interaction[M]. New York：Elservier Scientific Publishing Company，1979：202-205.

[15]杨学祥. 均布荷载下一端固定的文克尔地基梁的基底压力特性及其工程意义[J]. 工程力学，2006，23(11)：76-79. Yang Xuexiang. The Feature of Foundation Pressure on Winkler Foundation Beam with One Fixed End and Its Application[J]. Engineering Mechanics，2006，23(11)：76-79.

[16]周景星，李广信，虞石民，等. 基础工程[M]. 北京：清华大学出版社，2007：54-63. Zhou Jinxin，Li Guangxin，Yu Shimin, et al. Foundation Engineering[M]. Beijing：Tsinghua University Press，2007：54-63.

[17]龚晓南，褚 航. 基础刚度对复合地基性状的影响[J]. 工程力学，2003，20(4)：67-73. Gong Xiaonan，Chu Hang. The Influence of Base Stiffness on Status of Composite Foundations[J]. Engineering Mechanics，2003，20(4)：67-73.

（责任编辑：邓光辉）

Investigation on Load Distribution of the Joint of Cantilever Crossed Foundation Beam

Lin Liping，Luo Wan，He Jianqing
（School of Civil Engineering, Hunan University of Science and Technology，Xiangtan Hunan 411201，China）

Semi-infinite beam is extended from free end to infinitely long beam. Based on solutions for infinitely long beam on Winkler foundation, the shear force and bending moment at the free end of semi-infinite beam under the concentrated couples are derived. The external load applied at the free end is obtained by using the condition of the free end to meet zero moment and zero shear. The deflections at the action points are calculated separately under external loads and concentrated couples and the deflection at the action points are calculated under superposition of concentrated couples and external loads, and the calculation formula for cantilever influence coefficient with the action of concentrated couple is presented. According to the conditions of static equilibrium and deformation compatibility, general formulas for distribute load on joints of cantilever crossed foundation beams under vertical load and moments are given.

Winkler foundation；crossed foundation beam；semi-infinite beam；joint；load distribution

TU471

A

1673-9833(2015)02-0031-07

10.3969/j.issn.1673-9833.2015.02.006

2015-01-21

湖南科技大学研究生创新基金资助项目（S140009）

林丽萍（1989-），女（满族），吉林辽源人，湖南科技大学硕士生，主要研究方向为岩土工程，E-mail：1286979743@qq.com