一种高精度的配对安装轴承载荷计算方法
2015-12-07李文岩颜昌翔张军强
李文岩,颜昌翔,张军强
(中国科学院长春光学精密机械与物理研究所,长春 130033)
滚动轴承是采用滚动摩擦原理工作的支撑件,具有摩擦力小、易于启动、升速迅速、结构紧凑、标准化水平高、适应现代各种机械要求的工作性能和使用寿命以及维护保养简便等特点。它广泛应用于工业、农业、交通运输、航空航天和高科技等领域,与国民经济息息相关。全世界大约有80%的轴承应用于工农业机械、汽车、火车、飞机等运输设备中。各类主机的工作精度、性能、寿命、可靠性等指标都与轴承有着密切的关系,尤其是随着科学技术的发展,各类主机对轴承提出了很多特殊的要求,这些要求反过来又促进了轴承工业的发展,研制和生产出了很多特殊种类的轴承。轴承在国民经济发展和国防建设中发挥着越来越突出的作用,是制造产业链中的关键基础部件,体现国家制造能力和制造水平。
在实际工程应用中,许多零部件都包含配对安装的轴承,而配对安装的两轴承之间则相互作用、相互影响,其各自的载荷分布影响着对方的载荷分布和寿命。而针对配对安装轴承的载荷计算方法,相关的研究却很少。
1 方法原理阐述
以圆锥滚子轴承为例,圆锥滚子轴承在承受径向载荷的情况下,由于接触角的存在,会产生派生轴向力。当一对圆锥滚子轴承配对安装时,它们的派生轴向力方向往往相反,如图1所示。轴承I、II分别承受径向载荷Fr1、Fr2,所产生的派生轴向力分别为S1、S2。
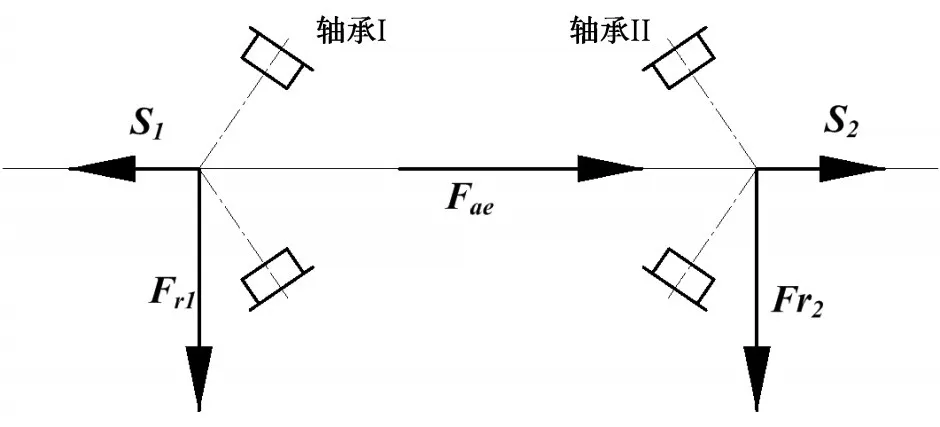
图1 圆锥滚子轴承轴向载荷计算
轴承I及II承受的轴向载荷可由下式求出[1]:
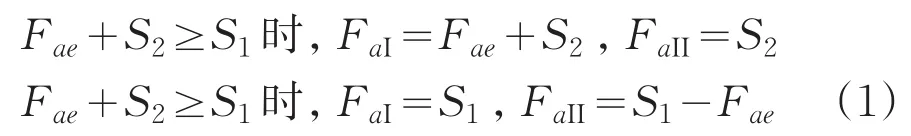
式中,FaI为轴承I所受轴向力;FaII为轴承II所受轴向力。
2 问题提出
配对安装的两轴承在径向载荷的作用下,会产生派生轴向力。传统方法计算派生轴向力大小时往往通过查询机械设计手册得到特定型号轴承的系数Y,并通过得到两轴承的派生轴向力值[2]。此方法认为特定型号的轴承在不变的径向载荷作用下产生的附加轴向力值大小不变,而不考虑滚子载荷分布的影响。
实际上,轴承的附加轴向力的大小是与轴承载荷直接相关的。如图2所示,当只有一个滚动体受载时:
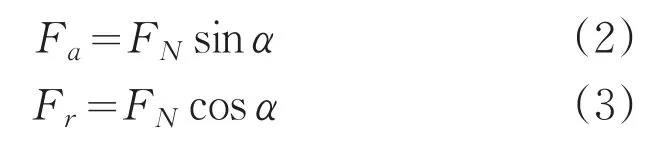
式中,α为轴承外圈接触角,Dgree;Fa为轴承所受轴向载荷,N;Fr为轴承所受径向载荷,N;FN为轴承滚子载荷,N。
则:

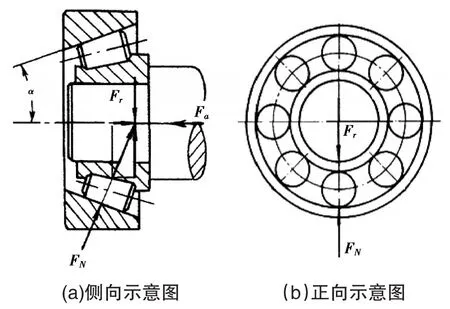
图2 轴承派生轴向力原理图1
当承载滚动体增多,即便径向载荷Fr相同,其轴向载荷也不同,如图3所示:
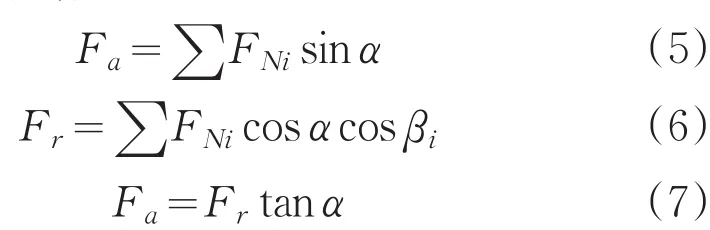
式中,下标i表示编号为i的滚子所对应的相应变量。
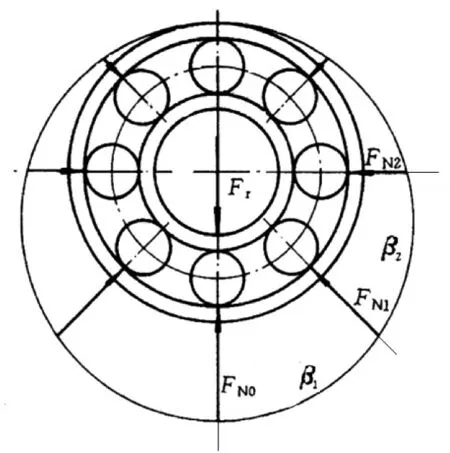
图3 轴承派生轴向力原理图2
当系统受到不同外界轴向力作用时,即便径向载荷恒定不变,各滚子承载情况也会不同,产生的附加轴向力也不同,而不能单纯的用一个系数来衡量附加轴向力的大小。所以,传统方法在精度上不够准确。
3 新方法计算过程
3.1 单个轴承载荷计算方法
在已知轴承所受轴向力以及径向力的前提下,根据Harris的滚动轴承理论[3],可以通过拟合积分过程,计算,查积分得到参数ε和J(ε)值,并r通过式(8)及式(9)得到轴承受载最大滚子以及各角度滚子所承受的载荷:
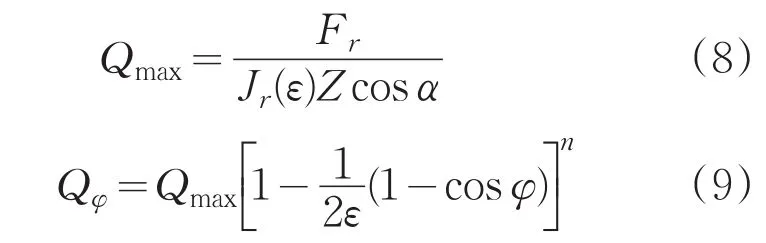
式中,α为轴承外圈接触角;Qmax为承载最大滚子所受载荷;Qφ为角度为φ的滚子所受载荷。
3.2 配对安装轴承计算方法
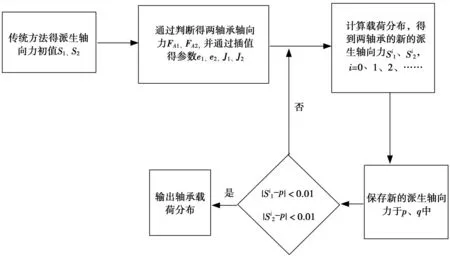
图4 配对轴承迭代计算流程图
单个轴承的载荷计算前提是已知的轴向载荷和径向载荷,而在两轴承配对安装的情况下,两轴承的径向载荷已知,而轴向载荷未知。两轴承在径向载荷的作用下各自派生一个轴向载荷并相互作用于对方,同时又受到预紧力,外界轴向力等力的作用,最终形成一个稳定的平衡状态。本文提出一种基于迭代的配对轴承载荷求解方法,通过给定两轴承的派生轴向力作为初值,并通过3.1节所述的单个轴承载荷计算方法进行迭代,进而求得配对两轴承的轴向以及径向载荷分布。其中轴承的派生轴向力初值可以通过查询机械设计手册得到轴向载荷系数Y,并通过得到。迭代的具体过程为:
(1)根据已知两轴承的径向载荷FR1、FR2,查询机械设计手册并计算得到的两轴承的派生轴向力值 S1、S2;
(2)以S1、S2作为载荷作用在轴承2、轴承1上并结合已知的外部轴向载荷Fae带入式(1)进行判断,得到两轴承所受的轴向力FA1、FA2;
(3)通过3.1节所述的单个轴承载荷计算方法计算并得到两轴承的载荷分布,即两轴承各个角度滚子的承载大小FNi,根据式(5)得到两轴承新的派生轴向力值,并保存于数组 p、q中;
(5)通过判断前后两次迭代的派生轴向力的差值来控制循环,直到两次的差值小于预设值0.01时为止;
(6)停止迭代,输出轴承载荷分布。
迭代计算流程图如图4所示。
3.3 单个轴承载荷计算方法验证
以32310轴承为例,通过有限元方法建立单个轴承模型分析计算[4,5],并与上述算法计算结果进行对比。为模拟轴承真实工况,取Gcr15钢的材料属性。在滚子与内外圈滚道、滚子与内圈挡边间建立了接触对;约束轴承外圈大端的轴向位移及轴承内圈与轴的配合面的径向位移;耦合轴承外圈外径圆柱面并建立pilot节点,通过pilot节点施加径向载荷11004N;在轴承内圈大端面施加轴向压紧载荷19621N。如图5和图6所示为有限元计算结果及两种算法的结果对比。其中,横坐标为滚动体数,0处为承载最大的滚子,顺时针方向滚动体数为正,逆时针方向为负。
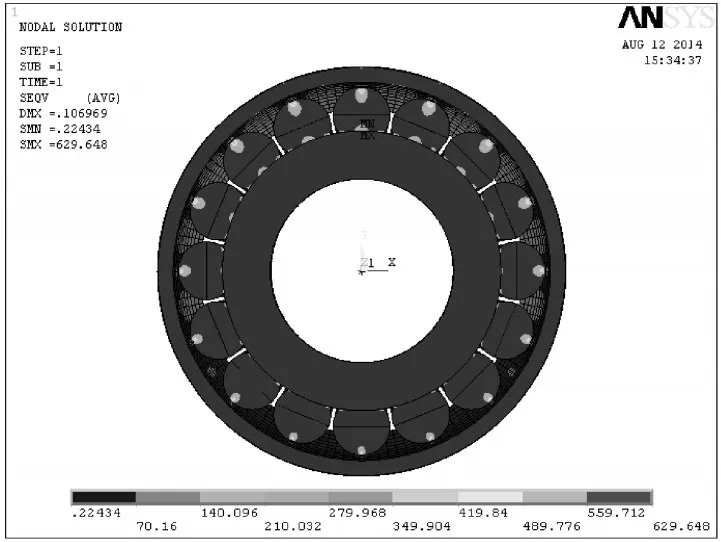
图5 单个轴承有限元计算结果
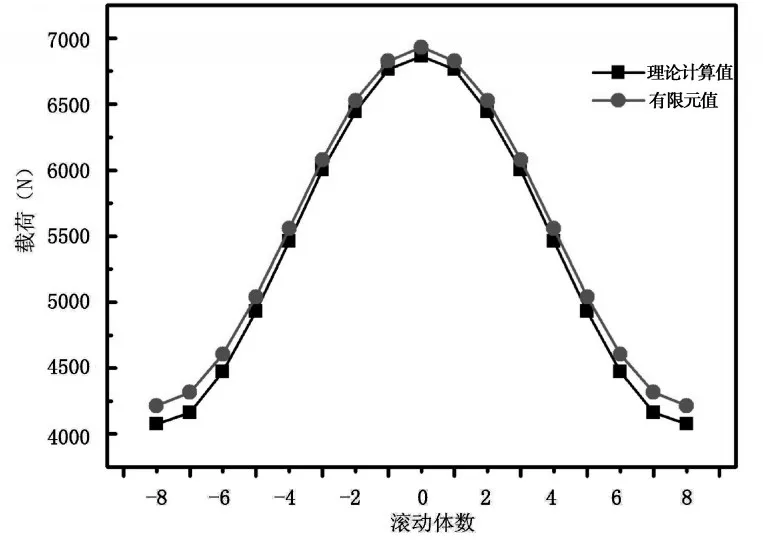
图6 两种方法的结果对比
通过对比可见,通过理论计算单个轴承在径向与轴向载荷作用下的载荷分布结果与有限元计算结果相差很小。
3.4 配对安装轴承计算方法验证
以轴承33220和33022组合为例在有限元软件ANSYS中建立了有限元模型,取Gcr15钢的材料属性。
本文在滚子与内外圈滚道、滚子与内圈挡边间建立了接触对,为模拟轴承的真实工况,约束两轴承外圈大端的轴向位移,绑定两轴承内圈与轴的配合面,同时约束轴的径向位移;耦合两轴承外圈外径圆柱面并建立两pilot节点,通过两pilot节点分别于33220轴承与33022轴承外圈施加径向载荷41561N和38439N,在33220轴承内圈大端面施加轴向预紧力14336N。计算分析得到计算结果,如图7所示。
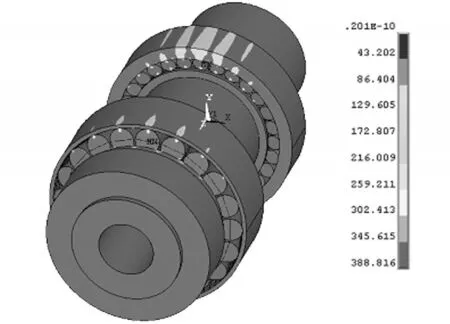
图7 33220-33022轴承有限元结果图
提取配对轴承的载荷计算结果,并对有限元分析结果与迭代结果及传统计算方法进行对比,如图8所示,其中,横坐标为滚动体数,0处为承载最大的滚子,顺时针方向滚动体数为正,逆时针方向为负。可以看出,迭代方法与有限元结果相差不大,而传统方法结果有一定误差,进而可以看出,迭代方法的精度是足够高的。
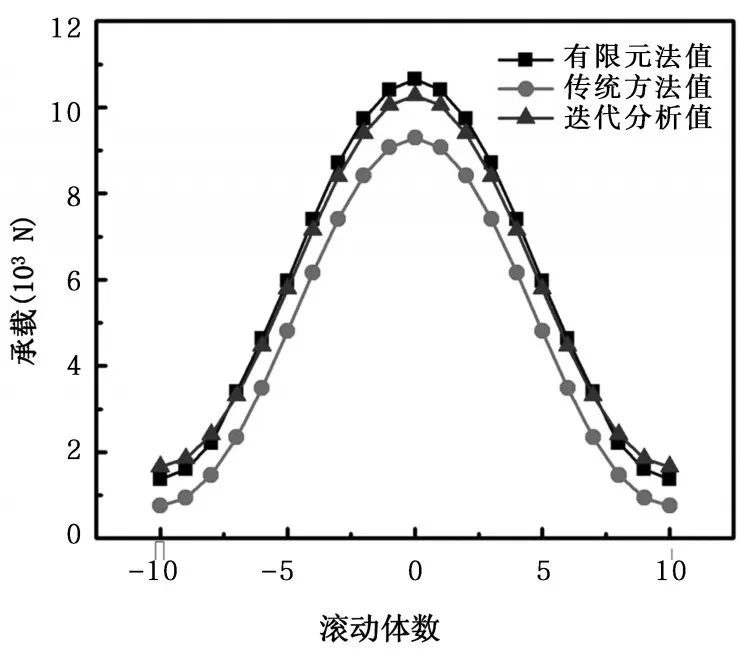
图8 33220轴承三种不同方法的结果对比图
4 结论
本文详细阐述了配对安装轴承在给定径向载荷下的作用原理,提出了一种配对安装轴承的载荷计算方法,并通过有限元方法进行了验证。对比可知,两种方法的计算结果相差很小,进而验证了配对安装轴承载荷计算方法的正确性。
[1]邱宣怀.机械设计[M].北京:高等教育出版社,2007.
[2]NSK滚动轴承手册[EB].日本精工株式会社,2009.
[3]Harris T A,Kotzalas M N,滚动轴承分析:第1卷[M].罗继伟译.5版,北京:机械工业出版社,2009:51-54.
[4]伍生.基于滚动轴承接触问题的有限元分析[D].内蒙古:内蒙古理工大学,2007.
[5]李峰,赵杰.应用ANSYS求解赫兹接触问题[J].机电产品开发与创新,2006,19(6):76-78.
