永磁同步电动机自适应逆控制系统设计

宫玉琳

（长春理工大学 电子信息工程学院，长春 130022）

交流永磁同步电动机控制系统广泛应用于工业、国防和社会生活的各个领域，重点应用场合如机器人、数控机床、雷达、火炮、航空装备、计算机外围设备、音视频设备等。研究高性能交流永磁同步电动机伺服系统控制策略，开发高性能交流永磁同步电动机伺服系统产品，对提高我国工业水平，促进国防工业发展，具有重要意义［1］。

自适应逆控制方法［2］通过对系统辨识得到被控对象的正模型，用被控对象传递函数的“逆”作为串联控制器，对系统的动态性能进行开环控制，因而避免了因反馈而引起的不稳定问题，同时又能做到对系统的动态特性的控制与对象扰动的控制分开处理而互不影响，提高了伺服系统的跟踪性能和抗干扰性能。但是，传统自适应逆控制策略由于受到非线性自适应滤波器的选取以及自适应滤波算法的影响，收敛速度和收敛精度存在矛盾，影响了控制效果。

本文将改进的径向基函数神经网络与FIR滤波器并联构成非线性自适应滤波器，引入自适应控制系统。同时，采用基于相关误差的变步长LMS算法对非线性滤波器的参数进行在线优化，提高了非线性滤波器的收敛速度和精度，精确辨识非线性系统正模型、逆模型并消除扰动，进而提高了自适应逆控制系统性能。仿真对比分析和实验结果表明，采用本文提出的自适应逆控制策略的永磁同步电动机系统具有良好的动态响应、稳态精度和较强的鲁棒性。

1 自适应逆控制

自适应逆控制系统的优势是将系统的动态响应与参数鲁棒性及抗扰性相分离，互不影响。主要由三个相互独立的部分组成，即对象辨识建模、对象逆建模（控制器建模）和自适应扰动消除环节，其结构如图1所示。

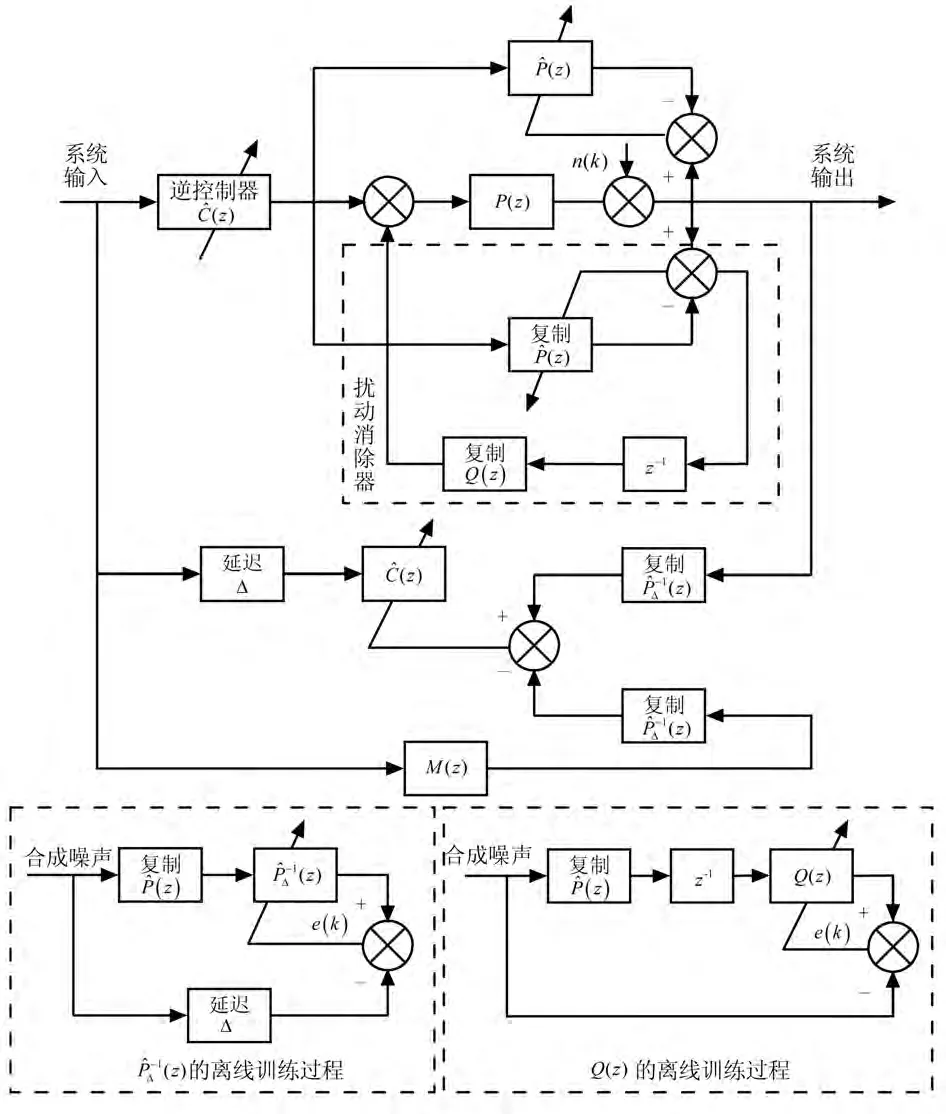
图1 自适应逆控制控制系统框图

自适应滤波器是自适应逆控制系统中的主要单元，用于对象建模、对象逆建模以及对象扰动消除。非线性自适应滤波器的结构以及自适应算法的实时性、收敛性能和稳定性直接决定了自适应逆控制的性能。

本文结合FIR滤波器和RBF神经网络的优点［3-5］，将RBF神经网络进行改进并与FIR滤波器相结合，构成了一种新型非线性滤波器，如图2所示。该非线性滤波器既继承神经网络的强大的非线性映射和逼近能力，又保持FIR滤波器具有的输出和权系数的线性关系，结合变步长LMS算法，可以快速而精确的实现非线性系统建模、逆建模及扰动消除器的设计，实现动态非线性系统的精确控制。

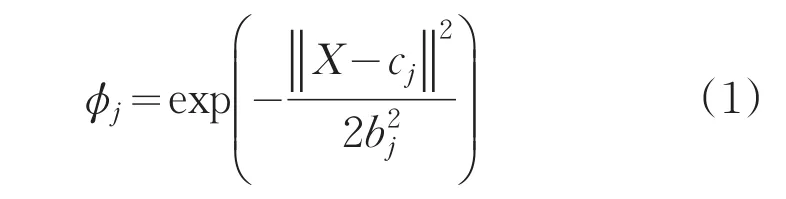
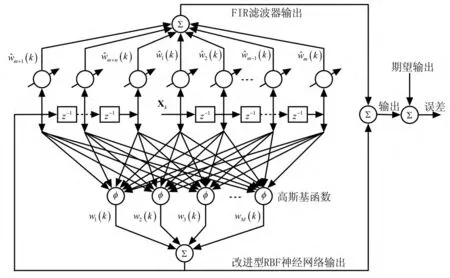
图2 改进的非线性滤波器

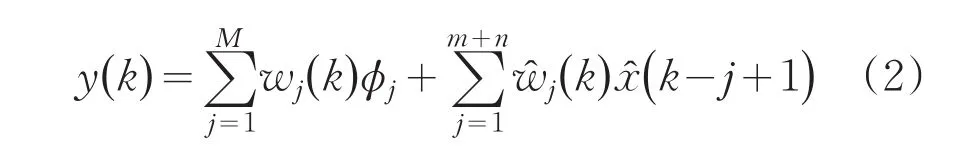
2 自适应学习算法

改进的RBF神经网络的节点中心向量c和节点基宽参数b的学习采用动量梯度下降法，即：

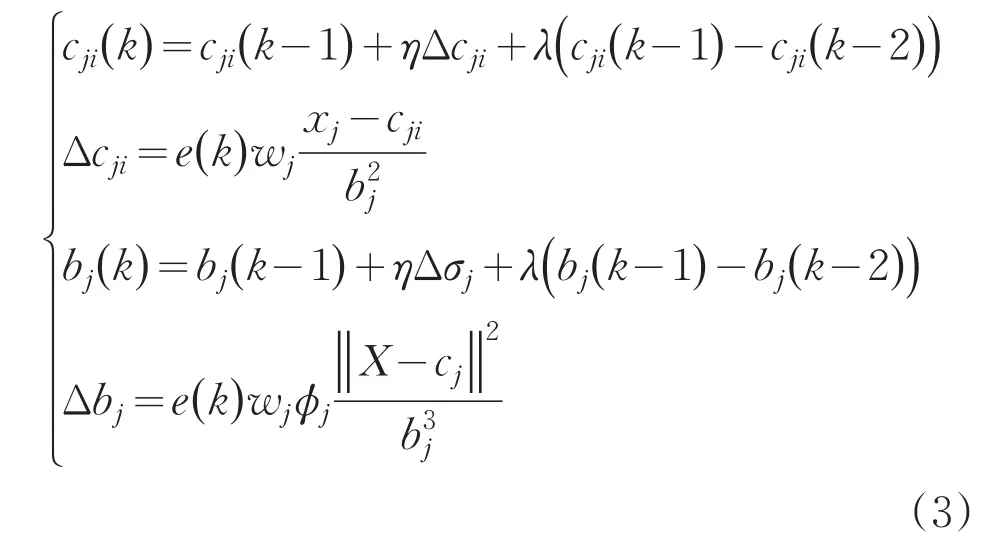
式中，η为学习速率，λ为动量因子，Δcji和Δbj为相邻两次迭代中，中心向量和节点基带宽参数的变化量。

控制器的权系数采用基于误差的变步长LMS算法进行修正，如下所示：

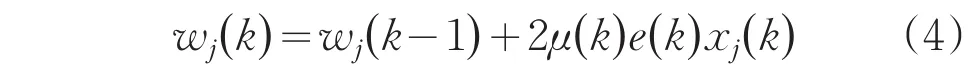
步长函数关系式如下所示：

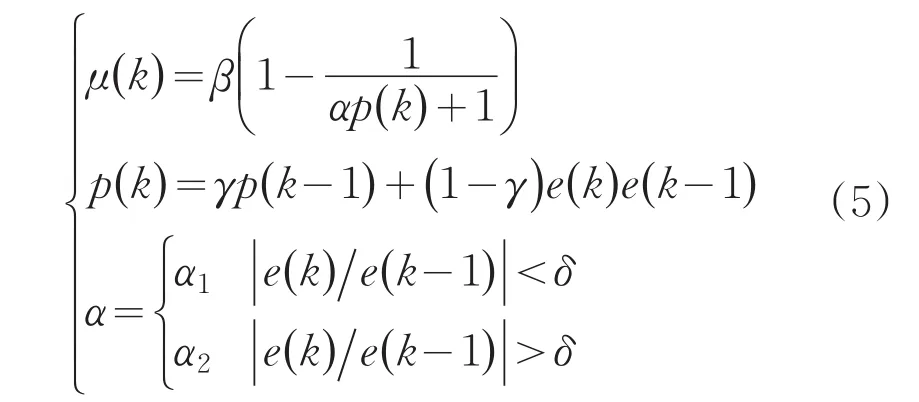
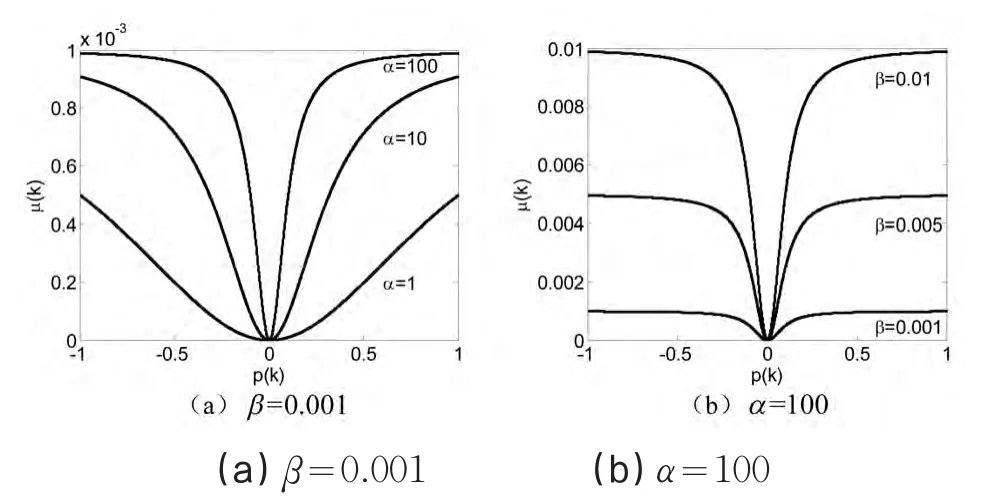
图3 不同参数对μ(k)的影响

由图3可以看出，在其它参数相同的情况下，如果α越大，步长取较大值的时间越长，算法的收敛速度越快。缺陷是e(k)趋近于0时，步长有陡峭的下降，这意味着很小的Δe(k)会导致很大的Δμ(k)，使算法的稳态误差增大。反之，如果α越小，步长取较大值的时间越短，算法的收敛速度越慢。因此，要获得较快的收敛速度，则参数α的取值应该较大，若要降低稳态误差，则参数α的取值应该较小。

在自适应过程中，控制器的性能指标函数为均方误差：

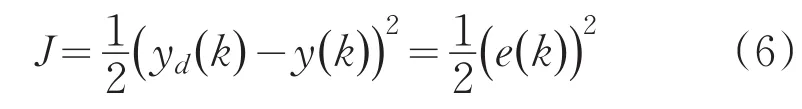
3 系统仿真与实现

自适应逆控制实现的永磁同步电动机控制系统仿真中，采用MATLAB/Simulink仿真，选用的永磁同步电动机额定电压138V，额定电流11A，额定转速2000rpm，定子电阻Rs=1.6Ω，极对数 p=2，d轴电感Ld=1.54mH，q轴电感Lq=1.54mH，转动惯量J=0.0156kg⋅m2。根据图1所示的自适应逆控制结构对永磁同步电动机进行建模与逆建模。

本文分别采用传统非线性滤波器和本文提出的改进非线性滤波器对永磁同步电动机系统进行建模和逆建模。改进的非线性自适应算法参数选取：α1=1，α2=100，β=0.05，δ=1.5，γ=0.8，η=0.35和λ=0.5。建模信号采用幅值为±1的正弦信号，逆建模信号取幅值为±1的白噪声，采样周期T=0.01s。仿真结果如图4和图5所示，从仿真结果可以看出，采用改进非线性滤波器建模和逆建模具有更快的收敛速度和辨识精度，效果明显优于传统非线性滤波器。

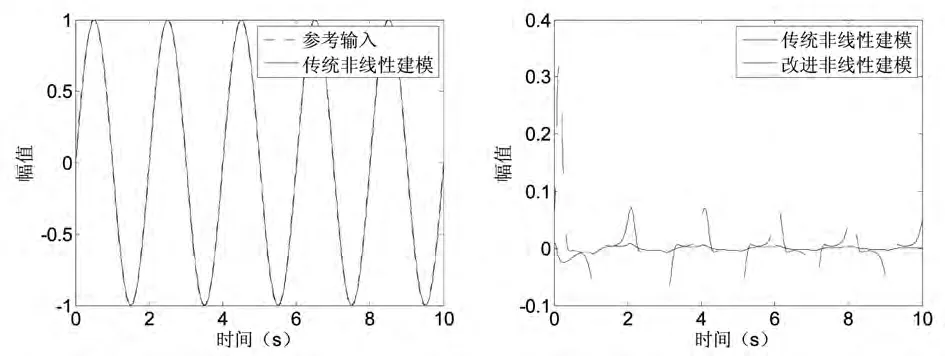
图4 建模输出和输出误差

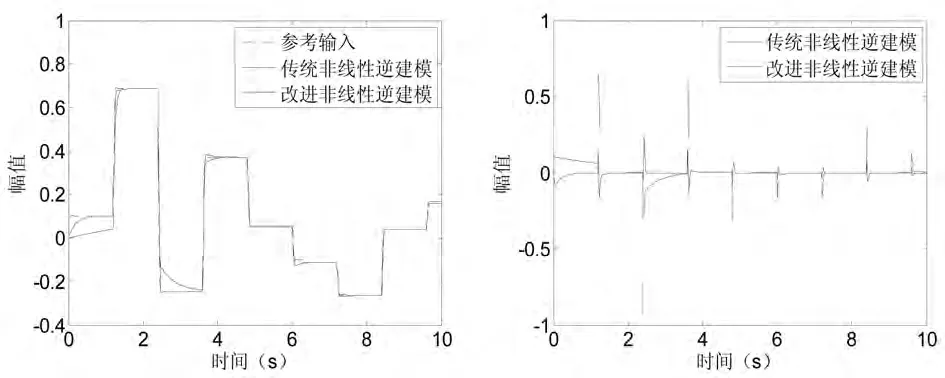
图5 逆建模输出和输出误差

图6和图7所示为采用传统自适应逆控制策略和本文改进自适应逆控制策略的输入输出比较。图6为系统不受外界扰动时的阶跃响应，可以看到改进自适应逆控制策略具有更好的动态响应和稳态精度。

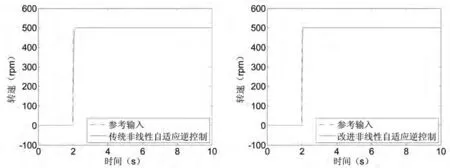
图6 系统性能曲线

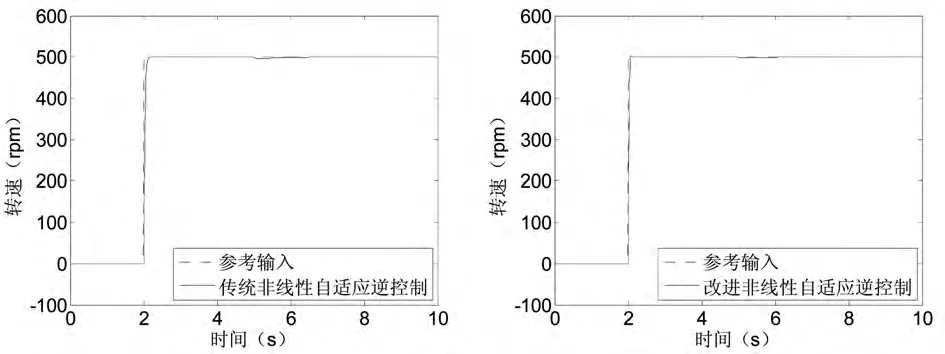
图7 参数变化时的系统性能曲线

为了验证系统的鲁棒性，在t=5s时，加入负载，如图7所示的负载变化时系统性能曲线。可以看到，改进自适应逆控制策略的系统，在受到外部扰动时，很快恢复到系统的设定值，基本没有影响，控制效果仍比较理想。而传统的自适应逆控制策略则受参数扰动影响较大，误差明显变大。可见，本文提出的自适应逆控制策略具有较好的鲁棒性。

4 结论

针对永磁同步电动机伺服这一非线性控制系统，提出了一种改进的自适应逆控制策略。采用改进的径向基函数神经网络与FIR滤波器构成非线性滤波器，并通过改进的自适应算法在线修正滤波器权值。仿真结果表明，本文提出的自适应逆控制策略优于传统的自适应逆控制，具有更高的控制精度和鲁棒性。实验测试表明，基于本文提出的自适应逆控制策略的永磁同步电动机伺服系统，提高了控制性能，具有较好的动态响应和稳态精度，可应用于机器人、数字机床等对控制精度要求较高的领域，具有较高的实用价值。

［1］郭庆鼎，孙宜标，王丽梅.现代永磁电动机交流伺服系统［M］.北京：中国电力出版社，2006.

［2］Bernard Widrow.Adaptive Inverse Control［J］.IFAC Adaptive Inverse Control and Signal Processing，Lund，Sweden，1986.

［3］柳晓菁，易建强，赵冬斌，等.一种基于RBF网络的非线性自适应逆控制系统［J］.控制与决策，2004，19（10）：1175-1177.

［4］韩华.基于LMS算法的自适应逆控制方法研究［D］.长沙：中南大学，2008.

［5］Yuan X F，Wang Y，Sun W，et al.RBF networks-based adaptive inverse model control system for electronic throttle［J］.IEEE Transactions On Control Systems Technology，2010，18（3）：750-756.

［6］李晓波，樊养余，白勃，等.双变因子LMS自适应滤波算法［J］.火力与指挥控制，2011，36（9）：42-45.

［7］J Moody，C J Darken.Fast learning in networks of locally tuned processing units［J］.Neural Computation，1989：281-294.

［8］TyseerAboulnasr，K Mayyas.A robustvariable step size lms algorithm：analysis and simulations［J］.IEEE Transactions On Signal Processing，1997，45（3）：631-639.

［9］TyseerAboulnasr，MayyasK.A robustvariable step size LMS-type algorithm：analysis and simulations［J］.IEEE Transactionson SignalProcessing，1997，45（3）：631-639.

［10］杜刚，战兴群，张卫明，等.基于改进型径向基函数网络的船舶非线性航向自适应逆控制［J］.上海交通大学学报，2006，40（6）：988-992.