基于数值解分析非均匀电场对离子迁移谱的影响
2015-12-07黄超群
刘 升,黄超群
(1.淮北师范大学计算机科学与技术学院,安徽淮北 235000;
2.中国科学院合肥物质科学研究院医学物理与技术中心,安徽合肥 230031)
基于数值解分析非均匀电场对离子迁移谱的影响
刘 升1,黄超群2
(1.淮北师范大学计算机科学与技术学院,安徽淮北 235000;
2.中国科学院合肥物质科学研究院医学物理与技术中心,安徽合肥 230031)
本研究分析了迁移管内带电体的结构,给出求解拉普拉斯方程的数学模型、迁移管带电体的边界处理方法和迁移管内离散电场数值的计算方法。离子门关闭期间,改变驱动脉冲的对称电压值将在迁移区产生非均匀电场,对离子迁移谱的分辨率、峰位、信噪比等特性产生影响。借助数值求解拉普拉斯方程得到的计算结果,对非均匀电场对迁移谱的影响进行合理的解释,给出理论计算迁移谱峰位的方法,并与实验结果进行比较,验证了计算方法的可靠性。实验结果表明,应用离散求解拉普拉斯方程计算迁移管电场在离子迁移谱领域有较好的应用前景。
拉普拉斯方程;电场计算;数值求解;离子迁移谱(IMS);离子门
拉普拉斯方程是一种二阶偏微分方程,求解拉普拉斯方程是工程领域常见的数学问题,如天文学、流体力学、电磁学等领域中经常需要通过求解拉普拉斯方程来描述引力场、流体场、电磁场等物理对象的分布情况[1-4]。
离子迁移谱(ion mobility spectrometry,IMS)是一种微量化学物质分析检测技术[5-6]。在大气压下工作,IMS具有探测灵敏度高、仪器成本低、操作简便等优点,已在化学毒剂、爆炸物、毒品和环境污染等检测方面得到广泛应用[7]。
离子迁移谱仪的基本工作原理示于图1。需要分析的样品被载气带入反应区,在离子源的作用下形成产物离子,这些离子在轴向电场的驱动下,通过离子门的控制进入离子迁移区。不同的产物离子在电场中的迁移速率不同,根据离子到达检测板的时间可实现对样品的分析和测量。

图1 离子迁移谱的工作原理Fig.1 Working principle of ion mobility spectrometry
离子的迁移速度在均匀电场中由公式v=KE决定,其中v是离子的迁移速度,E是离子所在区域的电场强度,K是离子迁移率。在低电场(小于1 000V/cm)情况下,K是常数,主要由离子的质量、结构、带电荷的多少以及迁移气体的种类决定。因为相同分子质量的物质其K值可能不同,所以离子迁移谱可以用来区分同分异构体。根据离子在气体中迁移的动力学理论[8],v是漂移离子的平均速度,是离子被电场加速的同时与迁移气体中分子碰撞的结果。
在简化的迁移管模型中,v是离子的平均速度,E是迁移管内的平均电场,可由迁移区的电势差和迁移区的长度计算得到。离子轨迹是基于迁移区平均电场进行描述的,但这种简化的迁移管模型是不精确的,因为离子的实际运动轨迹由迁移管内电场的分布决定,有时需要清楚的知道迁移管内每一点的电场大小和方向,特别是研究非均匀电场对迁移谱特性的影响时,计算迁移管内电场的分布非常重要。
迁移管内的电场由迁移环、离子门等带电导体形成,边界形状比较复杂,很难得到具体的解析式。应用数值计算法分析比较复杂的边界形状,应用有限差分法将连续的电场区域转化为离散数值来处理,可通过计算各离散点的电场数值,得到迁移管内电场的分布情况。
近年来,与离子迁移谱电场有关的文献主要是离子在近似均匀电场中的运动轨迹、离子通过离子门到达法拉弟板的动态过程、电场等因素对分辨率的影响等[9-11]。文献[12]提出了一种非对称离子门脉冲产生的方法,这与在常规离子门接法下形成的非均匀电场是不同的。
本研究应用数值求解拉普拉斯方程计算迁移管内电场分布,并对非均匀电场对离子迁移谱特性的影响进行解释,以阐明数值化求解迁
移管内电场分布对迁移谱分析的重要性。
1 数值化求解拉普拉斯方程计算迁移管内电场的方法
1.1 迁移管内电场的形成
迁移管内的电场由迁移环、离子门等带电导体形成,其结构示于图2。如果以o点为坐标原点建立坐标系,那么这个系统就具有轴对称性,可直接求解拉普拉斯方程计算电势,其通解为:
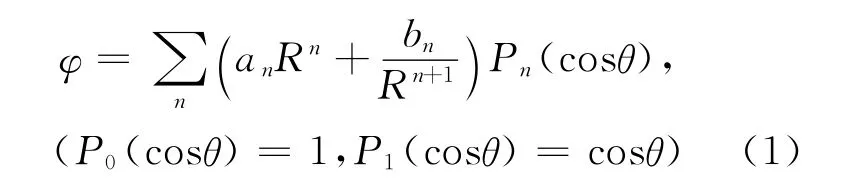
其中,R是带电导体上任意点到o点的距离,θ是带电导体上任意点到o点的连线与z轴的夹角。由于边界条件是迁移环和离子门的电势值,以及环的物理尺寸和间距等,理论上可以得到电势的解析式,但计算过程非常复杂。
1.2 有限差分法求解拉普拉斯方程
在整个迁移管中,如果不考虑带点粒子的影响,静电场只由带电导体决定,在空间中没有其他自由电荷分布。选择这些导体的表面作为区域的边界,则区域内部自由电荷密度ρ=0,电势满足的泊松方程可简化为拉普拉斯方程,即:

产生电场的电荷全部分布于迁移管内带电体的边界上,通过求解拉普拉斯方程满足边界条件的解可得到区域内电势分布情况。
在2D坐标系中,区域内任意点的电势满足拉普拉斯方程▽2u=0,将整个迁移管区域划分为许多矩形网格点,其中黑色矩形表示带电导体,示于图3。
将某一矩形点的电势定义为u(x,y),设相邻矩形点在x轴方向的间距为Δx,在y轴上的间距为Δy,则区域内任意点的电势满足[3]:

用差分代替偏导,得到:


图2 简化的迁移管带电体结构图Fig.2 Simplified structure diagram of charged conduct in drift tube

图3 迁移管区域的边界处理Fig.3 Boundaries process in region of drift tube
将式(4)和式(5)代入式(3),得到:
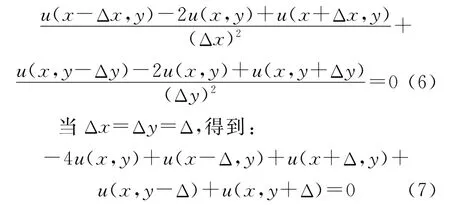
从式(7)可以看到,二阶偏微分方程∂2u/∂x2+∂2u/∂y2在一点的u(x,y)可以通过该点相邻的上、下、左、右4个点的离散值近似得到,采用直交网络形式的有限差分解法计算比较简单,要提高计算的精确度,就需要在求解区域划分比较密集的节点。还可以采用变步长的方式,即一部分区域节点较密,另一部分区域节点较稀疏,这样既提高了计算精度,也不会增加运算量。在实际计算中,如果对x轴方向或者y轴方向要求的精度不同,那么Δx和Δy也可以不同。
1.3 迁移管区域的边界处理和电场计算
拉普拉斯方程描述的是物理量随空间的变化规律,对于某一特定的区域,方程的解由物理量的初始值和边界值决定,这些边界条件是求解拉普拉斯方程的定解条件。图3所示的电场区域,已知的边界条件是迁移环和离子门的电压值。首先对区域边界进行处理,右边界接地,右边外围一列的所有节点电势为0。左边界的电势值由高压电源提供,电势值也是确定的。中间离子门由两组金属丝组成,每根金属丝的电势是确定的,每根金属丝是一个节点,由于金属丝之间的间距很小,金属丝与其他带电导体的距离较大,金属丝之间的节点电势可根据相邻的金属丝电势值插值得到。上下边界黑色矩形代表迁移环,有迁移环的地方电势也是确定的,利用两边迁移环的电压对迁移环之间的区域进行线性离散处理,这就确定了上下边界的电势值,这些节点称为固定节点。
对于边界以内的节点,首先假定一个初值,用计算机解题时,可取零值。按某一固定顺序依次应用式(7)计算每一节点的电势值,然后用新值代替旧值,完成一次迭代后,再进行下一次迭代,直到每一点计算得到的新旧值之差小于给定的精度。
只要每个节点的电势值计算完成,每个节点的电场大小均可以通过式(8)近似得到:

以上数值求解过程通过差商代替偏导数,应用Matlab等软件能够方便地求解拉普拉斯方程。
2 非均匀电场下,电场对离子迁移谱峰特征的影响
2.1 改变离子门接法形成迁移区非均匀电场
离子是在离子门脉冲的控制下从反应区断续地进入迁移区。离子门由两组金属丝组成,它们各自联通、相互绝缘、以交叉形式相互分开固定在支架上,离子门垂直于离子的运动方向。在传统的离子迁移谱中,离子门的接法示于图4,离子门的脉冲直接叠加到离子门的两端。

图4 常规离子门接法和驱动脉冲供电方式Fig.4 Conventional connection of ion shutter and pulse supply mode
在离子门通常的接法中,两端并联的电阻R1和R2的阻值相同。离子门关闭期间,两组
金属丝的电压分别为UA+Vd/2和UA-Vd/2(其中,UA是离子门所在平面处的电压值,Vd是离子门的脉冲幅度)。如果不考虑UA产生的电场,那么两组金属丝在迁移管内任意点产生的电场大小相等,方向相反,因此离子门两边的电场是近似的均匀电场。离子门开启和关闭期间,迁移管轴线上的电场也是近似的均匀电场,只是关闭期间离子门附近的电场发生了变化。
当电阻R1和R2的阻值不等时,在离子门关闭期间,两组金属丝对迁移管内任意点的电场影响不能抵消,迁移管内的电场会产生非均匀性。当R1的电压不等于R2的电压时,迁移管的轴线电场将会呈现明显的不均匀性。
2.2 数值化求解拉普拉斯方程得到轴线电场分布
应用有限差分法求解拉普拉斯方程得到的迁移管轴线电场分布的情况示于图5。迁移管在正高压模式下工作,离子门脉冲Vd=400V,R1的上端极性为正,R2的下端极性为负,R1上的电压为V1,R2上的电压为V2。由图4中的接线可知,离子门两组金属丝的电压分别是UA+V1和UA-V2,V1+V2=400V。实际上,V1和V2的极性不同,为了方便说明,V1和V2都作为数值来处理,写成了UA+V1和UA-V2。
图5中,横坐标30mm的地方是离子门所在位置,因为V1和迁移区高压同极性。当V1大于V2时,离子门右边的电场加强,离子门左边的电场减弱,离子门两边从左至右都呈现从大到小的趋势;当V1小于V2时则正好相反。
2.3 电场对离子迁移谱性能的影响
从上面的计算结果可以看到,离子门关闭期间,V1值大于V2值时,迁移区的电场被加强,迁移区电场从左至右呈现由强到弱的变化,而反应区的电场减弱,从左至右也呈现由强到弱的变化。V1和V2的作用结果,相当于在原来近似均匀的电场中,在离子门位置加入了一个对地电压为UA+(V1-V2)的金属网。离子门导通期间,UC=UB=UA,离子通过离子门的金属网进入迁移区,在迁移区内形成离子包。在离子包中的离子到达检测板的过程中,从图中轴线电场分布可以看出,离子包从左边到右边受到的电场力由大到小,对于同一类型的离子,如果位于离子包的左边,速率就大于位于离子包右边,因此形成的迁移谱就被压缩了。V1-V2的数值越大,离子峰被压缩的现象越明显。另外,离子门右边增强的电场会使迁移谱峰位右移。
V1值小于V2值时的情况正好相反。通过实验数据可以看到,电场对峰位、峰宽等的影响进一步影响了迁移谱分辨率等特性。

图5 改变V1和V2电压对迁移管轴线电场的影响Fig.5 Effect of changing V1and V2on electric field of axis in drift tube
3 理论计算结果与实验结果的比较
3.1 实验情况
实验装置自行搭建,迁移区包括6个迁移环和1块离子检测板,迁移环供电示于图4,迁移区长度6.3cm,迁移环内径25mm,外径35mm。离子门金属丝间距1mm,每组12根。迁移区电场为300V/cm,离子门脉冲宽度为250μs,迁移管在环境温度(21℃)下工作,迁移谱数据的采集周期是25ms,连续采集30次后对数值求平均值。实验中,通过改变R1和R2的阻值来实现V1和V2的改变,V1和V2的变化梯度是50V。
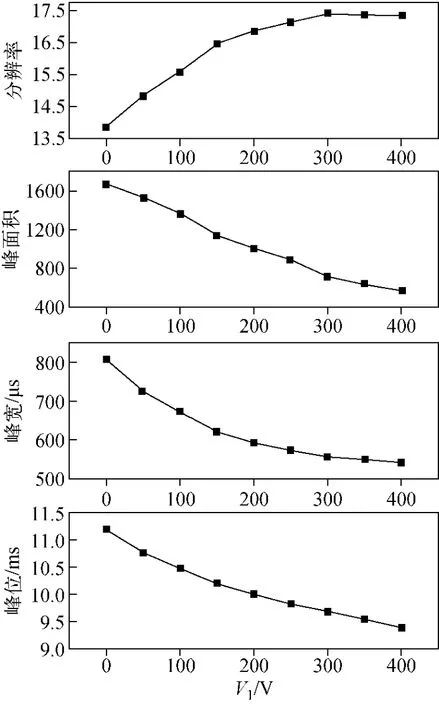
图6 V1对分辨率、峰面积、峰宽、峰位的影响Fig.6 Effect of V1on resolution,peak area,FWHM,peak position
改变离子门两端供电电压值V1和V2,在迁移区形成非均匀电场,对迁移谱的分辨率、峰面积、半峰宽、峰位的影响示于图6。随着V1的增大,峰位左移,半峰宽减小,峰面积减小,V1电压在300V处的分辨率最好。图5的计算结果可以清楚的解释离子门的电压对迁移谱的影响。离子门关闭期间,当V1>V2时,迁移区的电场增强,反应区的电场减弱,从左至右由强到弱变化,加强的电场缩短了离子的迁移时间,迁移谱峰位左移,迁移区的电场由强到弱变化,使得迁移谱的峰宽被压缩,迁移谱的分辨率随着V1的增大而得到改善,在V1=300V时,分辨率最好,这是因为V1增大,峰宽变窄,但迁移时间变短,使得300V处的分辨率最好。另外,V1-V2的值变大,通过离子门的离子数减少,信号强度减弱。
3.2 理论计算迁移时间并与实验数据比较
在匀强电场中,离子通过迁移管的时间为:

其中,d是离子门到法拉弟板的距离,δ是从离子门打开离子进入迁移区到离子门关闭瞬间形成的离子包的宽度,这个宽度由离子门开门的脉冲宽度决定,离子包中间的离子密度较大,两边离子较少,这样离子包将在迁移谱中形成两边对称的离子峰,所以峰顶对应的离子就是离子包中间部分的离子,离子包中部的离子走过的距离是,离子包的中心位置对应于峰的顶点,K是离子的迁移率系数。而在非均匀电场中,通过迁移管的离子迁移时间表示为:
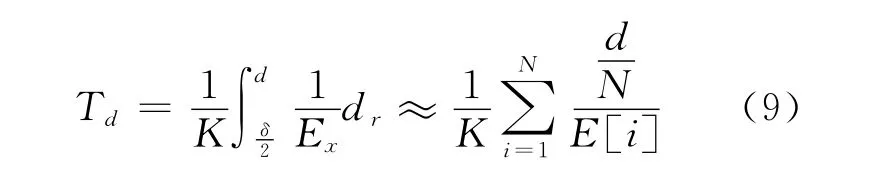

图7 实验得到的峰位和理论计算的峰位比较Fig.7 Comparison of the experiment peak position and theoretical peak position
式中的N将迁移区的长度离散化,即将d进行N等分,E[i]是通过计算得到的迁移管轴线上电场的离散数值。
理论计算的峰位和实际测量的峰位的数据比较示于图7。随着V1和V2的变化,两者变化
的趋势一致,但在理论计算的数据中,电场的变化对峰位的改变量大于实际的测量结果,最大误差在10%左右,因为实际测量的峰位还与迁移气的流速有关,这在理论计算时没有考虑到。
4 结论
离子迁移谱通过气态分子在电场中迁移率的不同实现对物质的分析,电场的分布决定着离子的运动轨迹,对离子迁移谱的特征影响很大,因此,计算迁移管内的电场分布情况对分析和研究离子迁移谱的特性非常重要。由于迁移管内的带电体分布较复杂,很难得到电场计算的解析式,因此,采用数值化求解拉普拉斯方程计算电场分布是有效的方法。
本工作使用数值求解拉普拉斯方程计算迁移区电场,是在没有考虑带电离子的空间电荷效应情况下来计算电场数据的。质谱或者离子迁移谱中的离子包和带电微粒对峰位和峰宽有着一定的影响,特别是大峰影响附近小峰的漂移时间和峰宽。如果考虑带电粒子的作用,那么迁移管内自由电荷的密度就不能为零,需要应用泊松方程或者其他方法。
改变离子门两端的控制电压的数值形成迁移区电场的非均匀性,电场的非均匀性影响离子的运动方向和速度,从而对迁移谱的峰宽、峰位、分辨率有较大的影响。离子门关闭期间两端电压不对称时,如果电压较高的一端与迁移高压极性相同时,峰位左移、半峰宽变窄、分辨率较好。如果电压较高的一端与迁移高压的极性不同时,峰位右移、半峰宽变宽、信噪比得到提高。实际应用中可以根据测量需要侧重于分辨率的改善或者信噪比的提高。应用数值化求解拉普拉斯方程得到迁移管内轴线的电场分布,可以很好地解释非均匀电场对离子迁移谱的影响。
[1] ROMANINI D,LEHMANN K K.Numerical Laplace transform density of states calculation for medium and large molecules[J].The Journal of Chemical Physics,1993,98(8):6 437-6 444.
[2] GÓMEZ P,URIBE F A.The numerical Laplace transform:An accurate technique for analyzing electromagnetic transients on power system de-vices[J].International Journal of Electrical Power &Energy Systems,2009,31(2):116-123.
[3] SADIKU M N O.Numerical techniques in electromagnetics[M].CRC Press,2000.
[4] CRUISE D R.A numerical method for the determination of an electric field about a complicated boundary[J].Journal of Applied Physics,2004,34(12):3 477-3 479.
[5] EICEMAN G A,KARPAS Z,HILL JR H H.Ion mobility spectrometry[M].CRC Press,2013.
[6] KARASEK F W.Plasma chromatography[J].Analytical Chemistry,1974,46(8):710a-720a.
[7] CLEMMER D E,JARROLD M F.Ion mobility measurements and their applications to clusters and biomolecules[J].Journal of Mass Spectrometry,1997,32(6):577-592.
[8] REVERCOMB H E,MASON E A.Theory of plasma chromatography/gaseous electrophoresis review[J].Analytical Chemistry,1975,47(7):970-983.
[9] NAZAROV E G,MILLER R A,EICEMAN G A,et al.Effect of the electric field strength,drift gas flow rate,and temperature on RF IMS response[J].Int J Ion Mobility Spectrom,2001,4(2):43-46.
[10]EICEMAN G A,NAZAROV E G,RODRIGUEZ J E,et al.Analysis of a drift tube at ambient pressure:Models and precise measurements in ion mobility spectrometry[J].Review of Scientific Instruments,2001,72(9):3 610-3 621.
[11]BRUNNER T,MUELLER A R,O’SULLIVAN K,et al.A large Bradbury Nielsen ion gate with flexible wire spacing based on photo-etched stainless steel grids and its characterization applying symmetric and asymmetric potentials[J].International Journal of Mass Spectrometry,2012,309:97-103.
[12]刘升,黄超群,沈成银,等.非对称离子门控制方法和对离子迁移谱分辨率的改善[J].光谱学与光谱分析,2013,33(11):2 881-2 885.LIU Sheng,HUANG Chaoqun,SHEN Chengyin,et al.Asymmetric control method for ion shutter and the resolution improvement of ion mobility spectrum[J].Spectroscopy and Spectral Analysis,2013,33(11):2 881-2 885(in Chinese).
Based on Numeric Solution Analysis of the Effect of Non-Uniform Electric Field to Ion Mobility Spectrometry
LIU Sheng1,HUANG Chao-qun2
(1.College of Computer Science and Technology,Huaibei Normal University,Huaibei 235000,China;2.Center of Medical Physics and Technology,Hefei Institutes of Physical Science,C.A.S,Hefei 230031,China)
First,the structure of charged conducts in ion mobility spectrometry(IMS)was analyzed and the mathematical modal of Laplace equation was given.Then the boundary process and the method of discrete electric field calculating of drift tube were given.Due to the non-uniform electric field produced by asymmetric power to ion shutter,the resolution,peak position and SNR of IMS was affected.Aimed by the result of numeric solution to Laplace equation,rational explanation was given for the effect of non-uniform to IMS.Theoretic calculation of peak position of IMS was achieved,and compared with the experimental results,the method reliability was verified.The experimental result proves that discrete solution to Laplace equation for calculate electric field in drift tube has good application prospect in the field of ion mobility spectrometry.
Laplace equation;electric field calculation;numeric solution;ion mobility spectrometry(IMS);ion shutter
O657.63;TH843
A
1004-2997(2015)02-0128-07
10.7538/zpxb.youxian.2015.0003
2014-05-12;
2014-08-26
污染控制与资源化研究国家重点实验室开放基金(PCRRF13024);安徽高校自然科学研究重点项目(KJ2014A225)资助
刘 升(1969—),男(汉族),安徽霍邱人,副教授,从事智能仪表和离子迁移谱研究。E-mail:liurise@139.com
黄超群(1974—),男(汉族),江西丰城人,副研究员,从事离子迁移谱与质谱技术研究。E-mail:cqhuang@aiofm.ac.cn
时间:2015-01-30;
http:∥www.cnki.net/kcms/doi/10.7538/zpxb.youxian.2015.0003.html
