RBF神经网络模型在遥感目标检测中的应用

赵世季

(上海民航职业技术学院 民航工程系，上海200232)

0 引 言

光学遥感成像是一种常见的成像方式，由于其形成的图像直观易懂，具有较高的分辨率，因此光学遥感图像具备SAR图像所没有的优势。而近年来我国海上舰船目标规模不断扩大，如功能越来越广泛的海洋调查船［1］、各种形态的海军战舰［2］等都相继涌现，对船舶的自动检测有利于监控特定海域的船舶交通、打击非法走私行为等［3］。

本文的识别过程包括图像分割、特征提取、识别分类3个步骤，主要针对6 种常见船舶的光学遥感图像进行检测，首先利用kmeans和区域生长法对图像进行分割，然后提取灰度一致性矢量、距离直方图2个特征，最后构建RBF神经网络模型对这6种常见船舶目标的遥感图像进行检测。

1 光学遥感图像预处理

在对图像进行分割之前，先利用高斯滤波去除图像噪声，由于船舶的光学遥感图像内容复杂，其中通常包括码头、陆地、海洋及船舶本身，另外图像在成像过程中受海况、雾、光照等多种不可控因素影响，形成的图像复杂多变，因此对于船舶的光学遥感图像通常采用由粗到精的分割方式。

本文首先利用kmeans法对图像进行粗分割，为确定聚类数，将整个图像数据集视为一个伪热力学系统，当图像被分割成k个类别时，称图像此时处于状态k。设置分割的初始状态为k = 1，在每个状态k，利用传统的kmeans 方法将图像分割为k 类，并定义此时的图像系统不稳定度为:

式中:fi(x，y)为图像第k个分割状态下的第i个子区域的灰度值;avei为第k个分割状态下的第i个子区域的平均灰度值。

由上面的定义可知，S 反映了图像在每个分割状态k 下的类内差异与类间差异的比值，S 越小，说明此时的分割状态越稳定。考虑到一般船舶的光学遥感图像中最多有4 类不同的物体，即本文中k的最大取值为4，使得不稳定度S 最小的k 值即为遥感图像的最佳聚类数。

在用kmeans法对图像粗分的基础上，求取每个子区域的灰度平均值，将此平均值作为区域生长法的种子点，根据欧式距离比较种子及其周围8 邻域像素点是否相似，若相似则将邻域像素点加入种子点所在区域，然后将新区域内的像素点作为种子点继续判断其邻域像素，直至没有任何满足条件的邻域像素，至此区域生长完毕。图1 给出了2 幅遥感图像的分割效果。

图1 分割结果Fig.1 Segmentation result

2 特征描述子

特征提取是海上目标识别的关键部分。为有效识别目标类型，特征需满足旋转仿射不变性、运算量低等特点。本文用灰度一致性矢量、距离直方图作为目标识别的特征。

2.1 灰度一致性矢量

灰度一致性矢量(GCVs)最为核心的问题就是对于连通域像素个数的统计。如图2所示，深色数字2 属于一个连通区域，该区域构成一个独立的子区域，统计出此区域的像素点个数，即深色数字2的个数，连通域像素个数的统计实际是树的前序遍历问题。对其他所有连通域都采用如上方式统计其像素个数，然后以连通域索引为横坐标建立连通域像素个数的直方图。

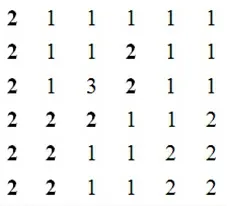
图2 连通域Fig.2 Connected region

关于灰度一致性矢量的一致性阈值选择问题，如人为设定某固定值，则有很大可能某个像素区间全被判为一致性区域，或者都为非一致性区域，因此本文定义阈值为:

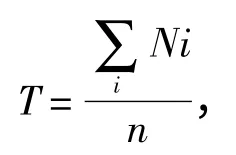
式中:n为第i 类灰度的连通区域个数，Ni为连通区域i的所有像素个数，当某一连通域中的像素个数大于T 时，判为一致性区域，否则为非连通性区域。

2.2 距离直方图

通常船舶目标的质心相对于目标边界各像素点具有位移和旋转不变性，据此可统计目标边缘上的各像素点到船舶质心的距离，并将其绘制成直方图，此直方图又称为距离直方图。该统计特征不仅有效地描述了船舶目标的形状轮廓，而且计算复杂度低。定义归一化系数为:

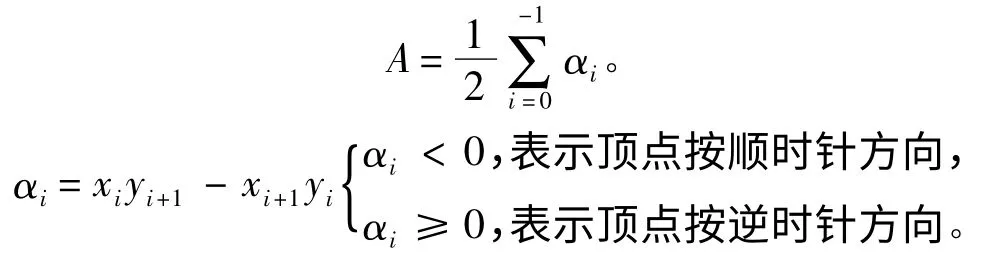
据以上公式，船舶目标的质心坐标表示为:

船舶目标的边缘像素点到质心的距离为:

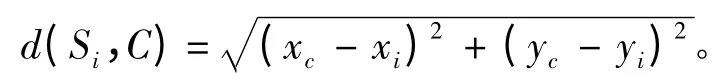
据此可生成距离直方图。为了使直方图具有尺度和旋转不变性，此处需将其归一化，即将直方图的每个柱除以整个直方图的最大值，使其归一化到0～1的范围。图3 给出了图1 中第1 幅图的距离直方图。

图3 距离直方图Fig.3 Distance histogram

3 RBF神经网络模型

3.1 RBF 网络结构

RBF 网(径向基函数神经网络)是一种前馈型神经网络［4］，通常网络只有3 层。图5为n个输入节点，h个隐节点，m个输出结点的n－h－m型结构RBF 网，网络中x=(x1，x2，…，xn)T∈Rn为输入矢量，Φi(* )为隐节点的激活函数，本文Φi(* )采用Gaussian 函数，RBF 网中的隐节点对输入通常具有局部特性，即如果输入离神经元的隐节点中心越远，则该隐节点对该输入的响应就越低，因此RBF 网的每个隐节点都具有一个数据中心ci，该ci决定了对于特定的输入，将有若干个神经元被激活，W∈Rh×m为隐节点的权值矩阵，b0，…，bm为输出节点偏置，y=［y1，…，ym］T为网络输出。图4 给出了常见RBF 网的网络结构。

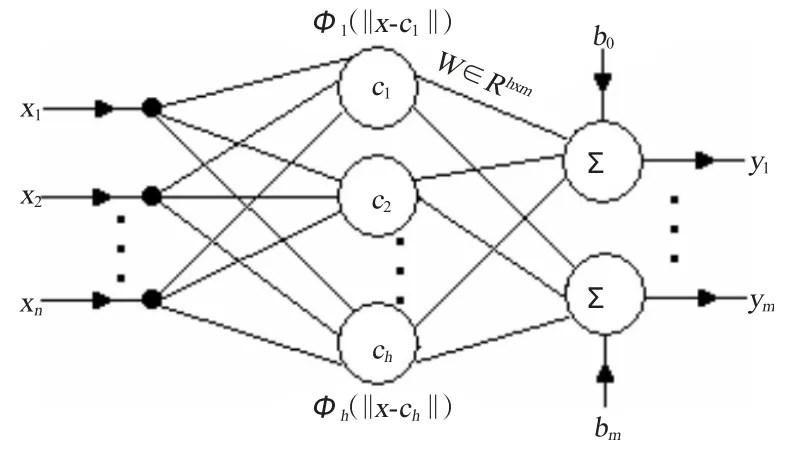
图4 RBF 网络结构Fig.4 Network structure of RBF

3.2 聚类学习算法

聚类方法作为最常用的RBF 网学习算法，其一般做法是先用无监督的kmeans 算法对输入样本进行聚类分析，从而确定各隐节点的数据中心ci，并依据相邻数据中心间的欧式距离确定各隐节点的扩展常数δi，然后隐节点的输出权值矩阵W和输出节点的偏移系数b 便可用常规的梯度法进行训练。

设训练的迭代次数为k，c1(k)，c2(k)，…，ch(k)为隐节点的聚类中心，w1(k)，w2(k)，…，wh(k)为其对应的聚类子域，则kmeans 算法步骤如下:

1)令k = 1，初始聚类中心确定为从总样本中随机抽出的h个不同输入样本。

2)计算各输入样本到各隐节点聚类中心的欧式距离。

3)对于输入样本Xj，将其归入与之距离最接近的中心点ci(k)，即当满足i(Xj)=－ci(k)‖，i = 1，2，…，h 时，Xj∈wi(k)。

4)利用新样本计算新的隐节点聚类中心:

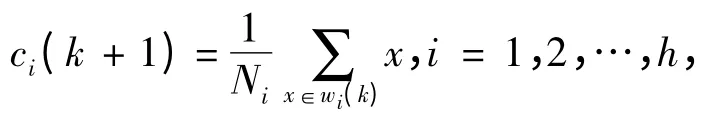
其中Ni为聚类子域wi(k)中的样本总个数。

5)当ci(k +1)≠ci(k)时，则转步骤2)，否则转步骤6)。

6)计算隐节点与其最相邻的隐节点聚类中心的范式距离作为当前隐节点的扩展常数δi= Kdi，其中K 称为重叠系数，即。

图5 给出了6 种船舶图像的部分输入样本经过上述kmeans 聚类后的结果，每种船舶类型10个样本，隐节点个数h = 6，由聚类结果可以看出，得到的6个数据中心各不相同。

图6 给出了训练误差随训练次数的变化情况，训练和测试数据集都来自美国海军研究院和美国海军武器中心，学习率η 取固定值0.02，目标误差0.01，初始权值和偏置均为(－0.1，0.1)之间的随机数。

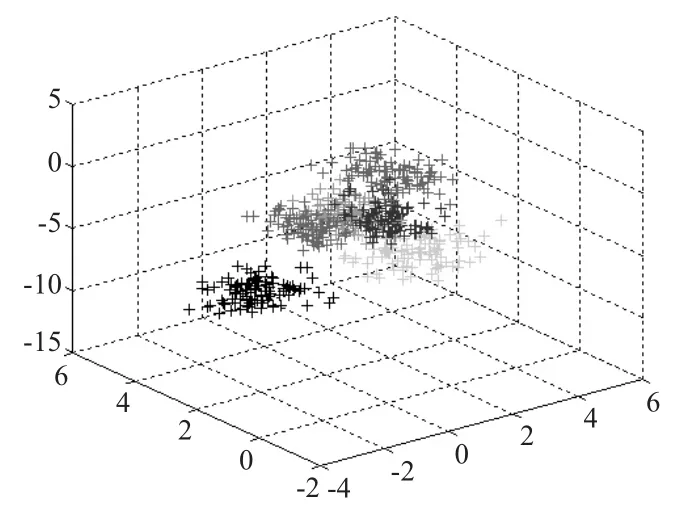
图5 聚类结果Fig.5 Clustering result

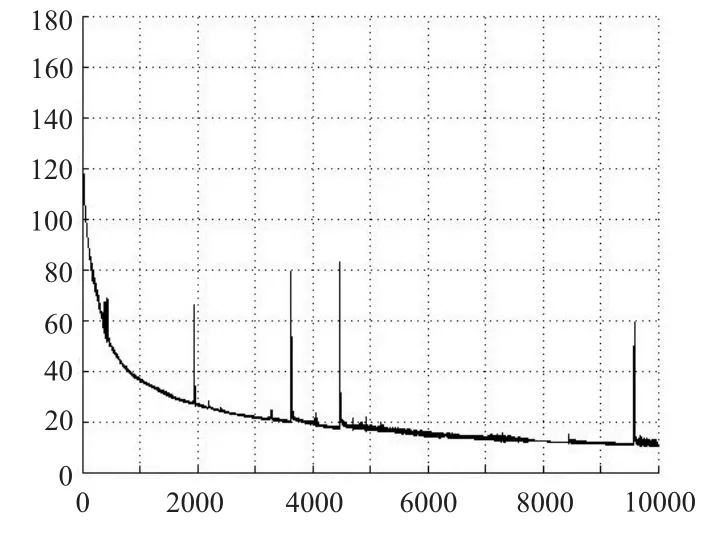
图6 训练误差曲线Fig.6 Training error

为排除识别结果的偶然性，本文共进行5 组独立重复试验。表1 给出了各重复试验下算法对每种船舶目标的检测精度。由表可看出，构建的RBF 网络模型对所有船舶的平均检测精度大约为86%。

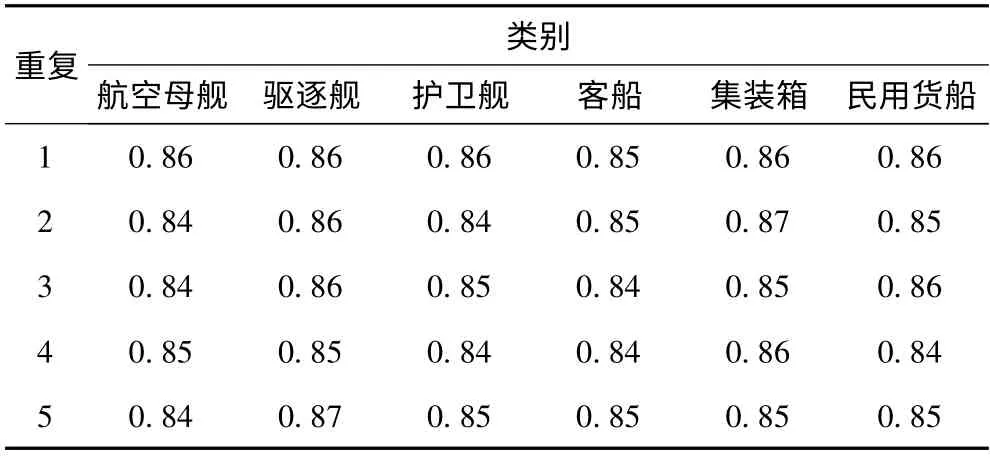
表1 分类精度Tab.1 Classification accuracy

4 结 语

本文利用RBF 网对6 种海上常见目标进行识别。结合kmeans和区域增长法对遥感图像进行分割，然后提取了目标区域的灰度归一化矢量和距离直方图2个特征。最后利用聚类学习对RBF 网络进行训练，并用其对船舶进行检测识别，准确率达到86%，有效实现了常见海船舶的检测。

［1］陈练，苏强，董亮，等.国内外海洋调查船发展对比分析［J］.舰船科学技术，2014，36(1):2－7.CHEN Lian，SU Qiang，DONG Liang，et al.The development and comparative analysis of ocean survey ship［J］.Ship Science and Technology，2014，36(1):2－7.

［2］熊正南，蔡开仕，武凤德，等.21世纪美国战略潜艇导航技术发展综述［J］.舰船科学技术，2002，24(3):30－37.XIONG Zheng-nan，CAI Kai-shi，WU Feng-de，et al.Review of submarine navigation technology of United States in 21st century［J］.Ship Science and Technology，2002，24(3):30－327.

［3］BURGESS D W.Automatic ship detection in satellite multispectral imagery［J］.Remote Sensing，1993，59(2):229－237.

［4］魏迎春，王金龙，马明涛.基于RBF神经网络的沉降槽泥层高度软测量模型研究［J］.中国仪器仪表，2010(1).WEI Ying-chun，WANG Jin-long，MA Ming-tao.Tank mud height measurement modeling based on RBF neural network［J］.China Instrument，2010(1).