MITS信息融合的船舶定位方法研究

郭 娟，刘 毅

(1.长江职业学院，湖北 武汉430074;2.中国船级社广州分社，广东 广州510235)

0 引 言

随着陆地资源的日渐匮乏，海洋资源越来越受到人们的关注与重视，相关海洋开发技术与设备也得到了快速发展。船舶深海作业作为重要的资源开采手段一直是人们研究的热点问题，而船舶定位技术［1］在深海资源开发过程中起着至关重要的作用，加之海运智能交通系统(MITS)在海洋领域的兴起，利用MITS和其他多源信息融合技术实现定位的方法为船舶动力定位提供新思路。因此，本文以船舶定位为研究对象，对MITS信息融合的船舶定位方法进行研究。本文结构安排如下:首先提出基于MITS信息融合的船舶定位方法，给出了系统流程的设计方案。然后对该方法中的关键部分进行详细介绍，主要包括以下3 部分内容:1)船舶动力定位的运动模型;2)一种多传感器融合的滤波方法，即自适应的平方根容积卡尔曼滤波算法;3)基于支持向量机的预测模型。

1 基于MITS信息融合的船舶定位方法

船舶动力定位系统通常由测量、控制、推进器3个部分组成［2］。在本文提出的方案中，基于MITS信息融合的船舶定位方法的系统流程如图1所示。

1)测量所用到的数据由MITS 内的信息及多传感器信息共同组成，MITS 内的信息主要包括船舶长度、宽度、排水量、舵高、舵面积等有关船舶自身的信息以及当前船舶运动的相关信息，多传感器包括位置、舵向、运动、风传感器。

2)控制部分主要通过信息融合方法对位置、舵向等进行估计，并通过前馈控制共同向推进器发出指令。

3)推进器主要作用是在得到控制指令后，根据指令驱动船舶的运动，以保证船舶在外力刺激的情况下依然正常作业。

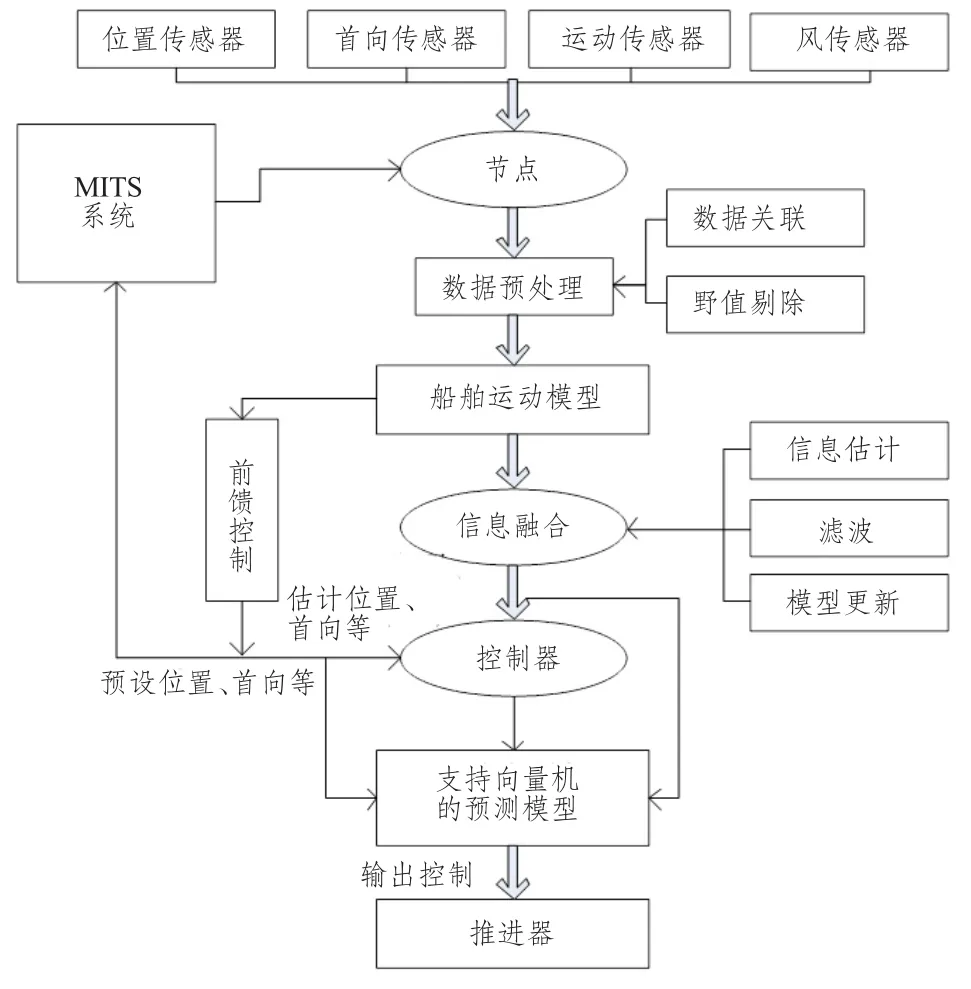
图1 系统流程图Fig.1 System flowchart

1.1 船舶动力定位的运动模型

本文主要研究在低速运动条件下的船舶定位问题，因此，船舶动力定位的运动模型采用CWNA (连续白噪声加速度)模型［3］。模型表示方法如下:

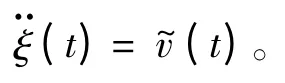
二阶的运动模型为:

其状态方程为:

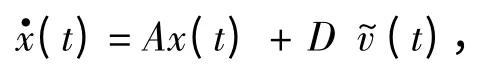
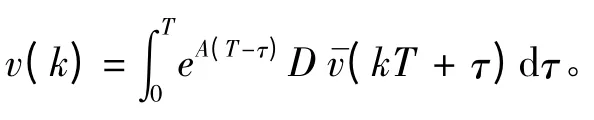
进而，船舶定位的运动模型为:

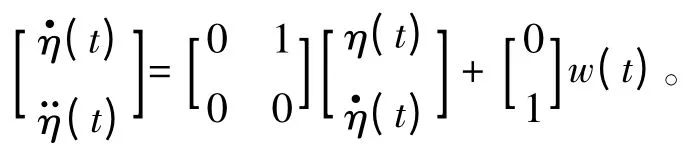
式中:w(t)表示均值为0的白噪声向量。

1.2 滤波方法

在船舶定位过程中，在相关数据信息进行融合之前必须做滤波的预处理，而滤波算法的精度和稳定性对系统的信息融合性能有着重要影响。为了提高滤波算法的鲁棒性，本文选用自适应的平方根容积卡尔曼滤波算法，即SRCKF 算法。SRCKF 算法过程［4］如下:

容积点为:

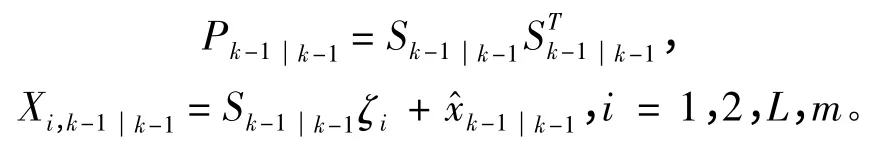
式中:m = 2n;ζi为母线(1，0，0，…，0)T元素置换得到的向量。

1)时间更新

式中:Qk－1=SQ，k－1，SQ，k－1为Qk－1的平方根系数;为加权的中心矩阵，表示为:

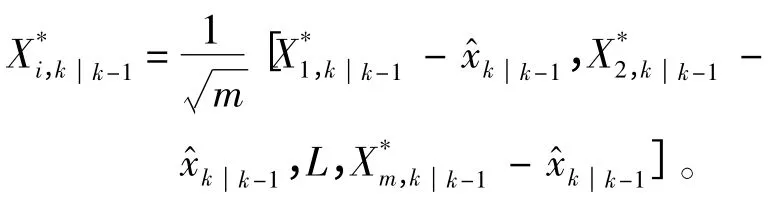
2)测量更新

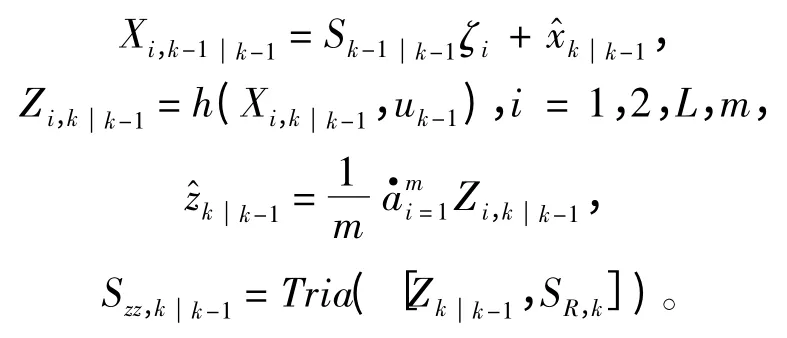
互协方差矩阵为:

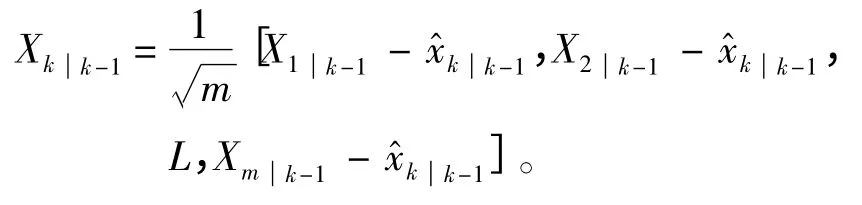
新协方差矩阵:

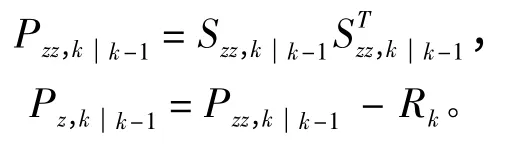
那么，k 时刻的滤波增益表示为:

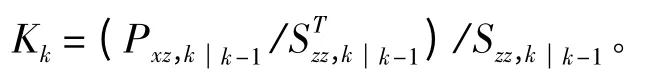
k 时刻的状态估计为:

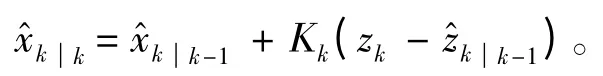
k 时刻的误差协方差阵的平方根系数:

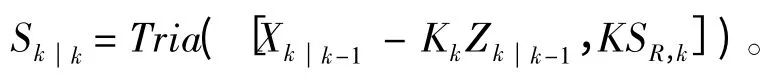
1.3 预测模型

支持向量机(SVM)是一种非线性预测技术，拥有很好的并行处理能力，并且自容错与自学习能力强，在复杂模型中得到了很好的应用，因此，文本采用支持向量机的预测模型。主要过程如下:

1)相空间重构

设定位系统中可测变量为x1，x2，x3，…，xM，M 表示数量，xi的时间序列表示为{xi，j}，j = 1，2，…，N。

设{xi，j}合并后的序列为Y，则:

重构的相空间为:

式中:τi为时间延迟;di为嵌入维数。设d 维空间上的光滑函数为F，则有:

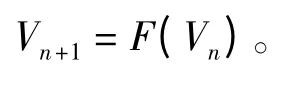
因此，有:

训练样本为的输入向量为:

输出向量为:

2)确定时间延迟参数

本文采用平均位移法确定时间延迟τi。

设x(i)与x(i + τ)的平均距离为Sm(τ)，则:

在Sm(τ)线性区域中，取末端对应的τ为最佳时延参数。

3)确定嵌入维数

本文采用平均误差最小化方法确定嵌入维数，设误差函数为:

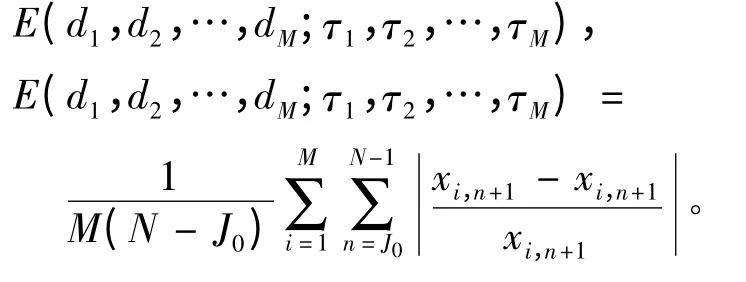
当E 取得最小值时，嵌入维数为最佳值。

2 仿真实验

本文的仿真实验主要针对横向和纵向的控制力进行测试，并且与最优二次型方法进行对比。实验数据如下:

1)训练数据

横 向 (× 103):4.79、4.11、0.86、6.94、6.46、2.0、－7.15、3.28、－8.11、0.97、14.68、－0.314、－3.15、－5.62、－7.56、－13.75、－3.45、0.98、－0.93、0.81;

纵向 (× 103):0.83、2.18、－1.25、5.43、－0.16、4.43、－1.91、3.46、1.65、0.5、3.92、－3.87、3.06、1.57、－1.89、－3.43、－0.44、1.2、4.04、3.42。

2)测试数据

横向 (× 103):－3.47、4.3、4.43、3.16、3.71、2.08、－2.49、3.15、1.63、5.68、6.77、－10.31、－2.19、－3.32、－1.29、0.33、－4.42、－3.02、－1.20、－9.15;

纵向(×103):－2.25、－2.78、－3.09、－0.83、2.72、1.08、－4.26、2.63、－1.94、3.19、1.34、－2.68、2.18、2.96、3.95、3.74、5.08、1.69、0.86、－1.35。

实验结果如图2～图3所示。

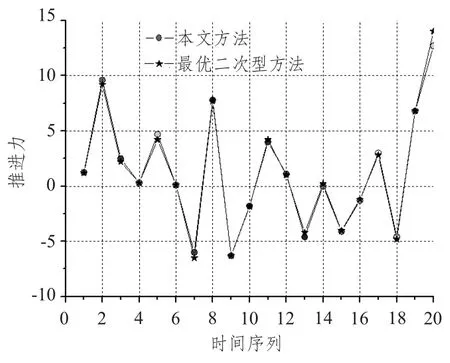
图2 预测误差(横向)Fig.2 The prediction error (Horizontal)

实验结果表明，本文提出的方法与最优二次型方法得到的推进力预测误差基本一致，因此，本文提出的方法具有可行性。

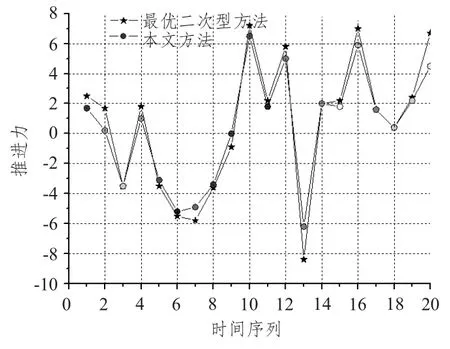
图3 预测误差(纵向)Fig.3 The prediction error (Vertical)

3 结 语

本文对船舶定位方法进行研究，提出了基于MITS信息融合的船舶动力定位方法，给出了系统流程的设计方案，并对定位的运动模型、多传感器融合的滤波方法以及预测模型等方法进行介绍。实验结果表明，本文提出的利用MITS信息融合的动力定位方法新颖且具有可行性。

［1］吴德烽，杨国豪.船舶动力定位关键技术研究综述［J］.舰船科学技术，2014，36(7):1－6.WU De-feng，YANG Guo-hao.Review on key techniques for ship dynamic positioning system［J］.Ship Science and Technology，2014，36(7):1－6.

［2］孙弢.多传感信息融合的船舶动力定位控制系统设计与仿真［J］.舰船科学技术，2014，36(12):116－119.SUN Tao.Design and simulation of dynamic positioning control system of vessels based on multi－sensor information fusion［J］.Ship Science and Technology，2014，36(12):116－119.

［3］YAAKOV B S，LI X R，KIRUBARAJAN T.Estimation with applications to tracking and navigation.New York:John Wiley ＆ Sons，Inc.，2001.

［4］ARASARATNAM I，HAYKIN S.Cubature kalman filters［J］.IEEE Trans.Automatic Control，2009，54(6):1254－1269.