基于PSO_SVM模型的水火弯板变形预测研究

李 彦，陈尤力，齐 亮

(江苏科技大学 电子信息学院，江苏 镇江212003)

0 引 言

为了尽快实现水火弯板加工自动化目标，水火弯板变形预测方面的研究十分必要。由于影响钢板成形的因素有很多，且众多规律都具有不确定性，因此建立合适的模型比较困难。传统上多采用Ansys 有限元软件计算水火弯板成形，但计算量过大，计算时间过长，不适合应用于自动化加工系统中。支持向量机(SVM)是一种新型的机器学习方法，它在统计学习理论和结构风险最小化理论的基础上，根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷，以期获得最好的泛化能力［1］。它能够根据水火弯板加工参数间的内在联系，建立动态的水火弯板预测模型来推断钢板的变形情况，具有很高的实时性。而支持向量机相关参数的选取对预测模型的精度有着非常重要的影响，一般采用网格搜索法，但这种方法需要根据人工经验来设置参数，而且运行时间比较长，效果也不是很好［2］。本文使用粒子群算法优化支持向量机的相关参数。

1 水火弯板变形机理

在水火弯板加工工艺过程中，热源的输入是影响钢板温度场的主要因素，而温度场的不均匀性正是导致钢板产生不同程度的残余变形的原因，最后钢板形成一定的弯曲形状。影响水火弯板最终变形量的几个主要加工参数、温度场和变形场的关系如图1所示。由图1 可知，由于热源是从钢板表面施加热载荷，然后通过热传导至厚度方向形成温度场梯度，即上下表面温度存在温差，最终导致钢板产生残余变形。因此，热源面输入对于钢板变形是个非常重要的影响因素。

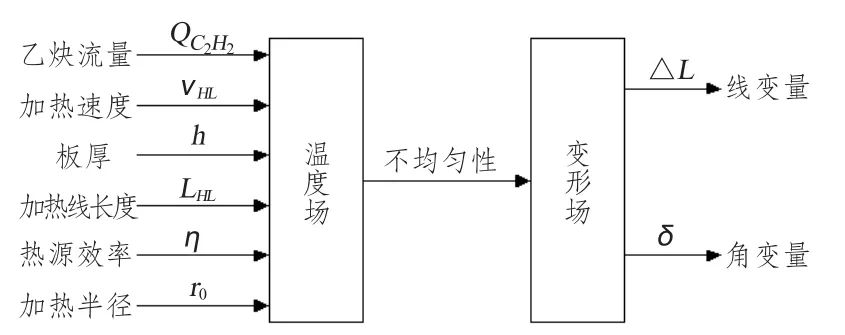
图1 温度场和变形场关系图Fig.1 Relationship between temperature field and deformation field

针对热源面输入影响因素，本文提出2个新变量qs和qs·t，旨在表征热源面输入的效果。其中变量qs是QC2H2(乙炔流量)、vHL(线加热速度)、η (热源效率)和r0(加热半径)等众多影响因素的函数，而qs·t是QC2H2，η，r0和LHL(加热线长度)等影响因素的函数，这2个复合变量反映了这些热输入参数所体现的综合效果。其数学模型如下:

在钢板的最终变形量问题上，利用线收缩变形量和角变形量来描述钢板的最终变形可以很贴近实际的钢板变形。最终，加工参数和变形量之间的关系如图2所示，这样可大大简化输入和输出的复杂性，同时也提高了输入和输出对应关系的准确性。

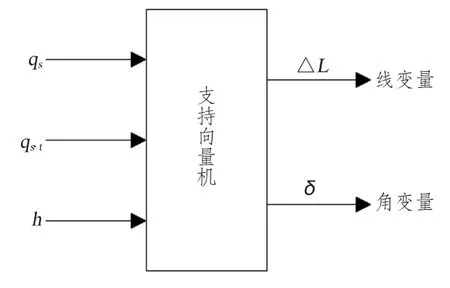
图2 复合变量和变形量的关系图Fig.2 Relationship between couple variable and deformation field

2 基本算法理论原理

2.1 SVM 原理

支持向量机(Support vector machine，SVM)又称为支持向量网络，它能较好地解决小样本、非线性和高维数等实际问题，已成为机器学习技术中最实用的方法之一，实质就是用线性的思维模式解决非线性问题，并成功地运用到分类、模式识别、回归和拟合等方面［3］。

对于回归问题，将低维空间非线性问题延伸到高维特征空间中建立线性回归函数:f(x)=ωφ(x)+b，ω为权值向量，φ(x)为非线性映射函数，b为偏差常数。

利用核函数代替点积运算，并引入拉格朗日乘子αi，最终得到SVM 回归模型为:

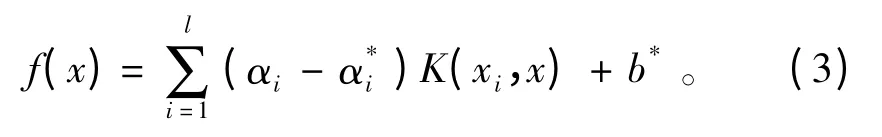
式中:K(xi，x)=φ(xi)φ(xj)为核函数。

RBF 核函数在低维、高维、小样本、大样本等情况下均表现出较好的学习能力，受到广泛应用［4］。因此本文将RBF 函数作为SVM的核函数。对于支持向量机，影响其性能的主要因素为核函数K(xi，x)及惩罚因子C的选择。因此，本文使用粒子群算法来优化支持向量机的相关参数。

2.2 PSO 基本原理

粒子群算法(Particle swarm optimization，PSO)是一种群体智能的优化算法［5］，PSO 初始化一群随机粒子，然后通过迭代找到最优解。在每次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，即

式中:d = 1，2，…，D为目标空间维数;i = 1，2，…，n为粒子的个数;k为当前迭代次数;Vid为粒子的速度;c1和c2是非负的常数，称为加速度因子;r1和r2为分布于［0，1］区间的随机数;ω为惯性权值，维持全局和局部搜索能力的平衡。

为提高算法的收敛速度，对惯性权值ω 进行线性调整，即随着迭代的进行，线性减少ω的值［6］，调整公式为:

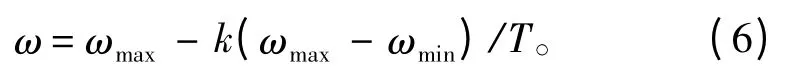
式中:k为当前迭代次数;T为最大迭代次数。

2.3 PSO_SVM 算法设计

支持向量机中参数的选取对回归模型的精度有一定的影响，从式(3)可明确看出，需要优化的参数是惩罚函数C和核函数系数g。本文选择PSO 算法优化SVM 参数，分别用2个粒子代表惩罚函数C和核函数系数g，主要步骤如下:

1)读取样本数据，对数据进行归一化处理，并建立训练样本和测试样本;

2)参数初始化，确定SVM 参数及粒子群算法的种群规模、加速度因子、最大迭代进化次数、惯性权值，并随机生成待优化参数粒子的位置和速度;

3)计算每个粒子当前的适应度值Pi;

4)比较粒子当前的适应度值Pi和该粒子的最优位置Pd，如果Pi优于Pd，则将Pi作为该粒子当前的最优位置;否则，执行步骤6;

5)比较粒子当前的最优位置Pd与该群体的最优位置Pg，如果Pd优于Pg，则将Pd作为当前该群体的最优位置;否则执行步骤6;

6)判断迭代次数或者最佳适应度值是否满足终止条件，如不满足终止条件，则进入步骤7;否则转入步骤8;

7)根据式(4)和式(5)更新粒子的速度和位置，返回执行步骤3;

8)输出最优参数，建立最优支持向量机预测模型，输入测试数据，进行实验仿真验证。

3 实例分析

3.1 数据处理

本文选取通过Ansys 有限元分析软件结合实验变形检测到的若干组数据，针对船舶通用材质低碳钢钢板进行不同加热温度的应力变形预测。随机选取40 组数据作为训练数据，剩下的5 组数据作为仿真测试数据。由于物理量的取值范围不同，同时也为了提高SVM 建模的速度，建模之前对数据进行归一化处理，取区间［-1，1］。

3.2 PSO_SVM模型建立

以Matlab R2010a为试验平台，利用台湾大学林智仁教授开发的LIBSVM 工具箱进行PSO_SVM模型的搭建与训练［7］。其中粒子群算法的参数设置为:选取固定大小的二维空间{(C，g)| C∈［0.1，100］，g∈［0.01，100］}，最大迭代进化次数为200，种群的粒子数量为20，加速度因子c1=1.5，c2=1.7，惯性权值ωmax=0.9，ωmin=0.4。

3.3 预测结果对比分析

图3～图5 分别是加热温度为700°，750°，800°时对应的钢板PSO_SVM模型预测集曲线。图中圆圈表示的是实际线变量和角变量值，三角形表示的是利用PSO_SVM模型得到的预测值，由图可知，水火弯板变形预测样本的实际目标值和预测值基本一致，数据分析后3 组线变量的复相关系数基本稳定在99.67%左右，3 组角变量的复相关系数基本稳定在99.32%左右，2个变形预测变量都取得了较好的拟合效果。

图3 700°时PSO_SVM模型测试曲线Fig.3 The PSO_SVM model test curve of 700°

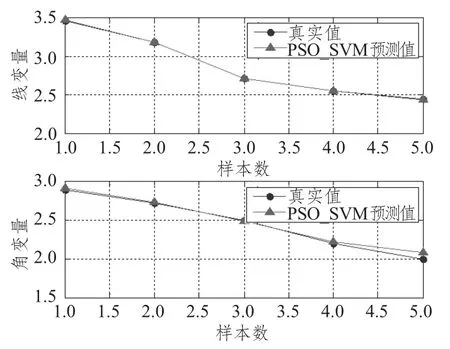
图4 750°时PSO_SVM模型测试曲线Fig.4 The PSO_SVM model test curve of 750°

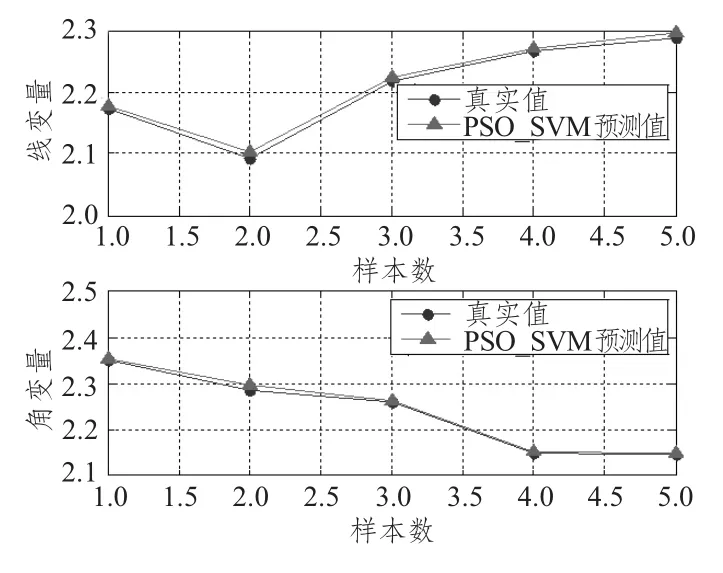
图5 800°时PSO_SVM模型测试曲线Fig.5 The PSO_SVM model test curve of 800°

为说明利用粒子群算法优化支持向量机相关参数的可行性及PSO_SVM模型预测的精确性，对上述的40 组训练数据和5 组测试数据分别用传统的支持向量机建模，并将测试结果进行对比分析，用误差百分比来评价预测精度(见表1)。从表1 可看出，PSO_SVM模型的预测精度要明显优于传统的支持向量机模型预测精度。其中，ΔL为线变形量，单位为0.1 mm，δ为角变形量，单位为1°。

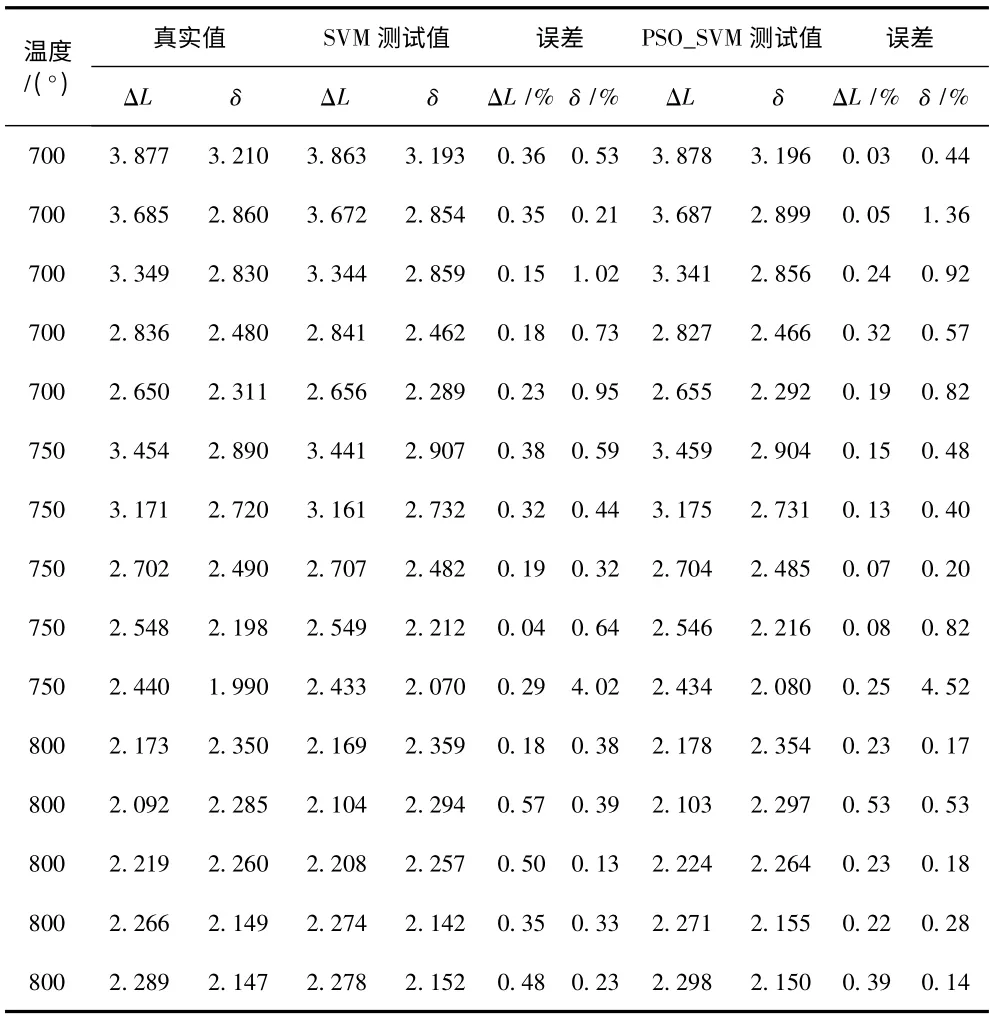
表1 测试结果对比分析Tab.1 Comparison of test results

4 结 语

本文构建了基于PSO_SVM的水火弯板变形预测模型，并利用粒子群对支持向量机的参数进行优化。仿真实验结果表明，基于PSO_SVM的水火弯板变形预测模型具有较强的可行性，相对于传统的SVM 预测模型而言，具有更好的预测精度，且泛化能力比较好，具有很高的实用价值。

［1］韩敏.混沌时间序列预测理论与方法［M］.北京:中国水利水电出版社，2007:203 -209.HAN Min.Chaotic time series forecasting theory and methods［M］.Beijing:China Water Power Press，2007:203-209.

［2］邓乃扬，田英杰.数据挖掘中的新方法—支持向量机［M］.北京:科学出版社，2006.DENG Nai-yang，TIAN Ying-jie.The new method of data mining-SVM［M］.Beijing:Science Press，2006.

［3］牛东晓，刘达，陈广娟，等.基于遗传优化的支持向量机小时负荷滚动预测［J］.电工技术学报，2007(6).NIU Dong-xiao，LIU Da，CHEN Guang-juan，et al.Support vector machine models optimized by genetic algorithm for hourly load rolling forecasting［J］.Transactions of China Electrotechnical Society，2007(6).

［4］高锦.基于SVM的图像分类［D］.西安:西北大学，2010.GAO Jin.Image classification based on SVM［D］.Xi′an:Northwestern University，2010.

［5］纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京:科学出版社，2009.JI Zhen，LIAO Hui-lian，WU Qing-hua.Particle swarm optimization and application ［M］.Beijing:Science Press，2009.

［6］MELGANI F，YAKOUB B.Classification of electrocardiogram signals with support vector machines and particle swarm optimization［J］.IEEE Transactions on Information Technology in Biomedicine，2008:667-677.

［7］WANG J，WANG W，WU S.A new support vector machine optimized by simulated annealing for global optimization［J］.2012.