像谜一样不可思议的数（下）

石头

“哪里有数学，哪里就有美”，数学中有许多新奇、有趣而又神秘的东西。现在，让我们一起去感受数学的魅力吧！

瞧，看似平凡而简单的“1”大哥自己和自己的组合，也能让人为之一惊。

1、11、111这样由1排在一起构成的自然数，被称为“重一数”。如果我们试着让这些“重一数”乘以自己本身，它们将会摩擦出什么样的火花呢？

1×1=1

11×11=121

111×111=12321

1111×1111=1234321

11111×11111=123454321

咦，你有没有注意到什么？

它们相乘的结果很有规律——按顺序，从1开始，逐渐增大到中间数位，而后又从中间数位逐渐减小到1。

如果这样的话，那么我们是不是可以预测111111×111111的结果呢？当然，根据规律这是可以做到的，结果是12345654321。如果这个结果让你有点儿难以置信，那就请你用计算器确认一下吧！

当你在为掌握了如此有用的规律而兴奋时，我不得不告诉你一个不好的消息。当1的个数超过10的时候，这条规律就不再适用了，因为超过10位数后，结果会发生进位的情况，所以到9位数为止的“重一数”的平方才符合“123……n……321”的规律。

其实，“重一数”还有其他有趣的规律。不信，你看！11在那里干吗呢？

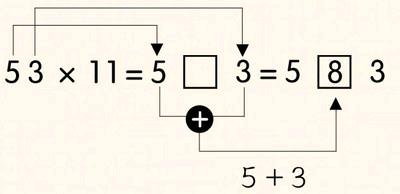
原来，在计算53×11时，我们只需要把十位数的5和个位数的3之和8放到5和3中间，就可以得到答案。

这条规律是不是放之四海而皆准呢？别急，让我们找63、64来试一试。63×11=693，完全正确;可64×11≠6104，这又该怎么解释呢？方法这么快就不适用了，真扫兴！哈哈，如果你观察得足够仔细的话，你应该已经看破其中的原理了。没错，64的十位数和个位数之和等于10，出现了进位。这时，我们得考虑进位的情况，所以我们有：

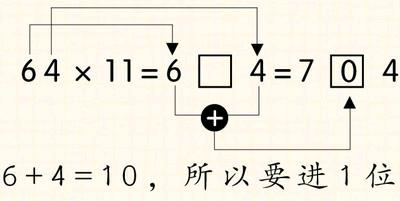
你是否注意到“12”跟我们非常有缘？

一年有12个月，一昼夜有12个时辰，时针在钟面上走一圈是12个小时，在我国和一些亚洲国家有着12生肖的说法，一打是12的单位，排球场上有12个运动员……怎么都是12？在生活中，12无处不在，我们被它所支配着、包围着。

12是数字王国中一颗闪着神奇光芒的明珠，它神奇的性质反映了数字的美妙，折射出数学的光彩。

如果你用数学的眼光来打量它，它的内涵和奇妙性质更会让你遐思和感慨。

首先，看它的数字结构，12是1和2的直接组合，这恰好表现了自然数的顺序。接下来，看它的因数。它的因数1、2、3、4、6、12，将前4个自然数全部包含，因此人们认为12是蕴含着内在秩序美的一个数，并且它的因数个数竟然是它数值的一半。

12的2倍是24，稍加联想，一年有24个节气，一天有24个小时;12的3倍是36，星宿中有36天罡星，兵法中有36计;12的5倍是60，每小时有60分钟，每分钟有60秒……如此种种，都给12披上一层神秘的面纱。

“8”与“发”谐音，因此它深受人们的偏爱，可偏偏有这么一个不识抬举之徒“缺8数”——12345679，它私自把8给“开除”了。你可能会说也没有0，可是将0放在首位，有和没有是一样的。这或许是人们不称它为缺0数的原因吧！可它为什么偏偏不要8呢？这真是让人想不通，人们开始对它产生兴趣，想要研究它一番。

你见过两个数相乘的积只包含一个数字吗？只含一个数字的积很少见，但是缺8数可以满足你。

12345679×9 =111111111                     12345679×45=555555555

12345679×18=222222222              12345679×54=666666666

12345679×27=333333333             12345679×63=777777777

12345679×36=444444444             12345679×72=888888888

看等号的右边，那让人惊叹的“清一色”。缺8数乘以9的倍数可以得到“清一色”。值得注意的是，当倍数超过81时，所得乘积将至少是10位数，这时我们需要对乘积进行变形，才能使它保持“清一色”。

12345679×243=2999999997

只要把乘积中最左边的2加到最右边的7上，或者把最右边的7加到最左边的2上，“清一色”就出现了。

你见过只有三个数字重复的乘积吗？告诉你！缺8数乘以3的倍数但不是9的倍数，就可以得到“三位一体”。

12345679×12=148148148                12345679×33=407407407

12345679×15=185185185                12345679×42=518518518

12345679×21=259259259              12345679×48=592592592

12345679×30=370370370             12345679×57=703703703

但当倍数超过78时，就得需要对乘积进行处理，才能重现“三位一体”。

12345679×84=1037037036

只要把乘积中最左边的1加到最右边的6上，或者把最右边的6加到最左边的1上，“三位一体”就出现了。

还有一个秘密，我猜你肯定不知道。缺8数实际上与某个循环小数是一根藤上的瓜。不信，你看！

=0.012345679012345679012345679……

看到了吧！缺8数竟然跟的循环节有关！

其实，像谜一样不可思议的数远远不止这些。数学是春天的一滴春雨，滋润大地;数学是夏日的太阳，充满激情;数学是深秋丰收的田野，带给人无限喜悦;数学是寒冬的一片雪花，洁白无暇。爱上数学，播下智慧的种子，继续去揭开它的神秘面纱吧！

（完）