一种基于子树分解的组播线性网络编码算法

刘宴涛，夏桂阳，徐 静，秦 娜

（渤海大学工学院，辽宁锦州121000）

一种基于子树分解的组播线性网络编码算法

刘宴涛，夏桂阳，徐 静，秦 娜

（渤海大学工学院，辽宁锦州121000）

针对拓扑不变网络的单源组播网络编码问题，基于子树分解提出一种新的线性网络编码算法。该算法由线图变换、子树分解、边不相邻路径搜索、全局编码矢量分配和局部编码矢量计算等过程组成。算法输入为满足组播条件的有向无环网络，输出为各边的全局编码矢量和局部编码矢量。在子树分解过程中，子树内部的边不需要编码，只对子树之间的边进行编码。理论分析和仿真实验结果表明，利用子树分解可以降低网络规模以及路径搜索和分配编码矢量的计算复杂度，缩短编码算法的运行时间，因此该算法是一种高效的单源组播网络编码算法。

线性网络编码；有向无环图；线图；子树分解；编码矢量

1 概述

网络编码的基本思想是在网络中传输数据包时，允许中间节点对收到的数据包进行组合、运算和编码等操作，从而生成新的数据包向后继节点发送。这与传统的路由技术有很大不同，因为路由采用存储转发的策略，不允许中间节点对数据包进行其他操作。与路由技术相比，网络编码技术带来了包括网络吞吐量、通信鲁棒性、无线带宽、能效节省、网络安全等收益［1］。为了换取这些收益，网络节点对数据包的处理功能要更为复杂，但随着集成电路和通信技术突飞猛进的发展以及摩尔定律的作用，现代网络通信的瓶颈越来越多地出现在通信信道的带宽上，而不是出现在网络设备的处理能力上，所以，网络编码技术将成为突破这一瓶颈的理想选择。

网络编码技术一经提出就引起了科学界和工程界的强烈兴趣，目前对该技术的研究主要从理论和应用2个层面进行。理论工作者热衷于探讨包括信息不等式［2］、网络编码的代数框架［3］、路由容量［4］以及编码容量［5］的性能极限、网络编码符号集的应用［6］、如何处理有环网络的延时［7］、非组播业务［8］中线性网络编码的不足以及网络纠错码［9］等理论问题。为分析这些问题，各种理论方法被应用在网络编码领域，其中包括信息论、代数、几何、图论、拟阵论、组合优化等。在工程应用方面，研究者纷纷提出各种编码方法将网络编码付诸工程实践，应用领域包括Ad Hoc网络、分布式存储、内容发布、网络纠错、P2P网络等［1］。编码方法包括线性编码［7］、非线性编码［8］、随机编码［10］、多项式时间编码［11］、子空间网络纠错码［9］、标量编码和矢量编码［12］等。对网络编码的综述性介绍可见文献［1-2，13］。

本文从工程应用方面出发，针对拓扑不变的单源组播网络提出一种基于子树分解的线性网络编码算法（Linear Network Coding Based on Subtree Decomposition，LNCBSD），通过子树分解的预处理过程把网络图缩减为子树图，利用静态子树集和动态子树集的方法为每棵子树分配全局编码矢量，并进一步计算局部编码矢量。

2 相关研究

文献［14］论证了网络编码与路由相比的优点，证明了当网络拓扑满足从源节点到各个接收节点的最小割的最小值等于h时（本文称此为组播条件），如果允许中间节点进行编码且符号取自足够大的有限域，则可以实现从源节点向多个接收节点同时组播h个符号。该文献的工作相当于把单播应用中的最大流最小割定理［15］推广到了组播应用中，这是路由技术所无法完成的。基于文献［14］的工作，文献［7］提出在有限域上进行线性运算即可实现组播，从而提出了线性网络编码（Linear Network Coding，LNC）的概念，虽然后来也出现了非线性编码的概念，但线性编码由于其编译码的简单性依然作为主流的编码方法。文献［3］把网络编码问题转换为代数问题，把网络的输入输出用转移矩阵联系起来，从而可以应用状态变量方程或矩阵完成等方法解决编译码问题。文献［8］举反例证明在非组播应用中线性编码是非充分的，并讨论了矢量编码和非线性编码的作用。文献［10］针对拓扑可变的无线网络提出了随机编码的方法，其基本思想是在每个中间节点处随机产生本地编码矢量，并且在发送正式符号之前，先发送h个单位矢量的符号，这样在接收节点处就可以获得全局编码矢量，从而进行译码。这种方法最大的问题是额外开销问题，其降低了网络利用率，而且全局编码矢量的计算对网络传输错误非常敏感。文献［11］针对组播应用提出了一种多项式时间复杂度的线性网络编码方法，把网络编码向工程应用中推进了一步，该方法的时间复杂度是O（|E||T|h（h+|E|））。其中，|E|表示边数；|T|表示接收节点数；h表示源节点组播的符号数，这种算法的复杂度的上界函数是边数的平方，因此，是一种多项式时间算法。与之相比，本文算法复杂度的上界函数是网络中子树数的平方，因此低于文献［11］方法的复杂度。文献［16］另辟蹊径，对系统转移矩阵采用迭代的矩阵完成的方法计算编码矢量，该方法的计算复杂度为O（|E|3|T|log|E|）。文献［17］提出了网络的子树分解的概念，并基于子树分解提出了射影几何编码的分布式方法，该方法把子树的全局编码矢量设计成射影线PG（n，q）上的射影点坐标，从而保证了不同路径上子树的编码矢量的线性无关性。本文也使用了子树分解的方法，但本文是通过建立静态子树集和动态子树集，并在子树上动态推进，为各个子树分配全局编码矢量，由于分配全局编码矢量时要考虑不同路径上子树的线性无关性，因此本文算法是一种拓扑依赖的确定性方法。需要说明的是，文献［17］方法虽然在分配编码矢量时是分布式的，不需要考虑其他节点的矢量分配情况，但子树分解时依然是拓扑依赖的。文献［18］研究了对有噪网络进行随机线性网络编码的问题，设计一种信道模型把随机错误建模为对码字的扰动，并提出了一种基于随机稀疏图的纠错码的编解码方法。文献［19］针对多组播组的分组竞争问题，提出了一种分组调度算法用以最小化所需的同步缓冲器大小。文献［20］应用博弈论的方法分析了多重单播无线网络中，当节点独立地选择各自路由时的传输次数代价问题，求得了最好和最差稳定解的限，并提出了一种优化的代价共享协议。

从2008年开始，网络纠错码成为网络编码领域的一个热点研究方向。网络纠错码把网络编码和纠错码相结合，用网络编码的空间冗余度代替纠错码的时间冗余度，实现纠错的功能。在网络纠错码中具有代表性的是文献［9］提出的一种基于子空间编码的方法，该方法利用线性随机网络编码的子空间不变性（即发送矢量张成的子空间和接收矢量张成的子空间是同一个子空间），在发送端发送子空间的基矢量，在接收端根据收到的矢量计算子空间，并根据子空间距离进行最小距离译码。这种方法实现了非相关网络编码功能，发送和接收节点不需要知道网络结构，也不需要如文献［11］中数据包的额外开销。文献［21］针对组播应用中数据丢失问题，提出了一种可靠组播算法，通过数据包分代传送和网络编码相结合的方法完成数据恢复。文献［22］采用M arkov链的方法分析了单播应用中随机线性网络编码的时延特征与有限域大小的关系。文献［23］给出了网络编码的序列矩阵描述方法，从而把确定性编码、随机编码和卷积编码统一在一个框架内，并提出了一种多项式时间的译码方法。

3 线性网络编码

本文讨论的问题和方法属于线性网络编码的范畴。首先规定：本文讨论的网络属于有向无环图（Directed Acyclic Graph，DAG），节点之间靠单位容量的有向边相连接，节点之间允许多边存在，且网络中没有环路。网络中有一个源节点S向网络中发送h个符号σ1，σ2，…，σh，这些符号产生于有限域GF（2m），即σ1，σ2，…，σh∈GF（2m）。网络中存在多个接收节点Ri等待接收这些符号。网络的拓扑结构满足组播条件，即源节点和每个接收节点之间的最小割都大于等于流量h。

如图1所示，在对满足组播条件的网络进行线性网络编码时，中间节点收到来自入边的符号后，在每个出边输出一个新符号，这些输出符号分别由输入符号的某个线性组合得到。具体地说，对于某个中间节点t，假设t的入边集合为｛e1，e2，…，，出边集合为，则出边e′j上的符号f（e′j）和所有入边上的符号f（ei）之间靠本地编码矢量｛l1j，l2j…，l|IN（t）|j｝，lij∈GF（2m），联系起来［2，15］，即：

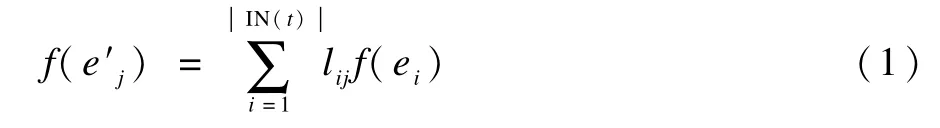
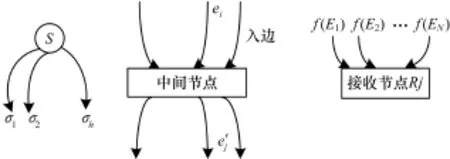
图1 线性网络编码示意图

进一步不难发现，由于各个中间节点都执行线性运算，因此在网络中各个边E上流动的符号f（E）又可以看成是源节点s发出的符号σ1，σ2，…，σh的线性组合，即：

称（g1，g2，…，gh），gh∈GF（2m）为边E的全局编码矢量。

每个接收节点收到来自入边E1，E2，…，Eh的h个符号f（E1），f（E2），…，f（Eh）后，通过在有限域GF（2m）上求解线性方程组可得源节点发出的h个符号σ1，σ2，…，σh。因为线性方程组：

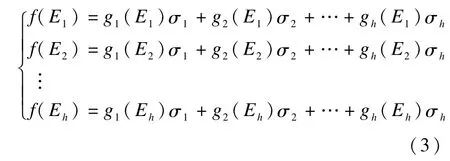
有解的充要条件是系数行列式（4）满秩，所以，线性网络编码问题就等价于如何为网络中各个边分配全局编码矢量，使得在各个接收节点处系数行列式（4）满秩的问题。

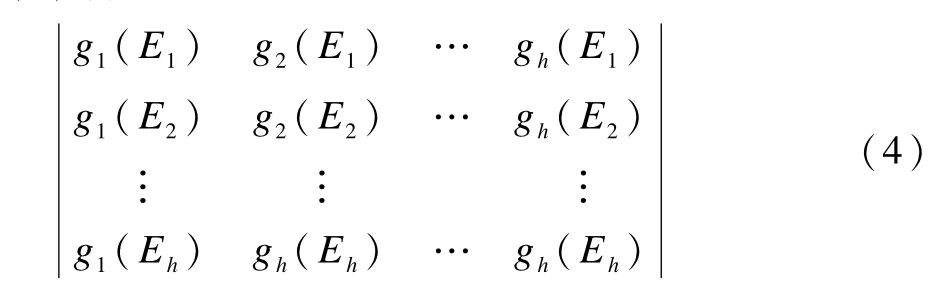
在应用线性网络编码时，为了减小问题的规模和编码的复杂度，一个思路是当网络中某个节点仅有一个入边时，这样的节点只需要转发收到的符号，不需要进行编码，即采用传统路由的方法。基于这样一种考虑，本文提出了一种基于子树分解的组播线性网络编码算法，该算法把网络分解为若干棵子树，子树内部不需要编码，或者说子树内部的所有节点使用相同的全局编码矢量。然后为源节点S到每个接收节点Ri之间寻找h条不相邻子树路径，并进一步为这些路径上的子树分配全局编码矢量。

4 LNCBSD算法

4.1 算法说明

本文算法的输入是一个满足组播条件的单源多宿组播网络拓扑图，输出是网络中各个边的全局编码矢量和本地编码矢量。算法分为5步执行：（1）由原网络拓扑图生成与之相对应的线图；（2）对线图做子树分解得到子树图；（3）为每个接收节点Ri分配静态子树集SRi；（4）维护动态子树集DRi，为每棵子树分配全局编码矢量；（5）由全局编码矢量计算得到编码节点的局部编码矢量。

具体过程如下：

（1）把原始的网络拓扑图变为线图［15］。所谓线图就是把原图中的边表示成线图中的节点，如果原图中一条边的箭头和另一条边的箭尾共享一个节点，则在线图中这2条边变成的2个节点相邻接。需要说明的是如果原图中源节点发出的符号个数是h，在线图中将出现h个源节点；如果原图中接收节点的数目是N，在线图中将出现hN个接收节点，即每个接收节点将扩展成h个分节点。

（2）对线图进行子树分解［17］。子树分解是指把线图分解成若干棵子树，每棵子树的树根只能是线图中的源节点或具有多个输入边的节点（称为编码节点），且子树结束于接收节点或另一个编码节点。这样分解后，每棵子树内部将流动相同的符号，因此在子树内部不需要编码，仅仅进行转发的操作。另外，每个接收节点的h个分节点将位于h棵不同的子树中。经过子树分解后，原本复杂的线图可以缩减为由子树之间相连接构成的子树图。

（3）在子树图中，从h个源节点到每个接收节点Rj的h个分节点之间一一对应地寻找h条边不相邻路径，存入一个静态路径集合SRj里，这些路径的存在性是被组播条件所保证的。因为共有N个接收节点，所以静态集合也有N个。但是需要说明的是，虽然每个接收节点的h条路径不相邻接，但各个接收节点之间可能会出现路径的邻接，也就是说某个接收节点的某条子树路径和其他接收节点的某条子树路径可能会共用某个中间子树。

（4）为每棵子树分配全局编码核。其中，由于h个源节点所位于的h棵子树内部流动的是原始符号σ1～σh，所以这h棵子树的全局编码核可以分配成h个单位矢量（0…0，1，0…0）T，其中，第i个分量为1，其他分量为0。除了源节点所位于的h棵子树外，其他子树的全局编码核动态地生成。不失一般性，假设源节点所位于的h棵子树编号为T1～Th，为了给某个子树分配编码矢量，需要为每个接收节点Rj维护一个动态集合DRj，其中存放的是当前正在编码的SRj各条路径最前端的子树Ti以及该子树的全局编码矢量g（Ti），共h个。随着编码的进行，集合DRj中存放的h个子树沿着SRj的各条路径动态地向前推进。

给子树Ti分配编码矢量时遵循的原则是其全局编码矢量g（Ti）和同一动态集合中其他h-1个全局编码矢量要彼此线性无关。也就是说，要保证接收节点Rj的h条不相邻路径上子树的全局编码矢量彼此线性无关。另外，由于子树Ti可能位于多个接收节点的路径上，因此这个线性无关的原则要保证对所有接收节点的动态集合都成立。

（5）根据所有子树的全局编码矢量计算得到各个编码节点的局部编码矢量。不失一般性，假设子树T有m个父子树节点T1，T2，…，Tm（一个子树的父子树是指与本子树相连接，且从信息流上看位于本子树上游的子树节点。），则这些子树的全局编码矢量和局部编码矢量（l1，l2，…，lm）的关系满足［15］：

由于每个全局编码矢量g（Ti）都是h维矢量，因此式（5）实际是一个由h个方程构成的方程组。如果该方程组的h×m维系数矩阵（g（T1），g（T2），…，g（Tm））的秩r=m，则在有限域上求解该方程组，即可得到子树T的局部编码矢量（l1，l2，…，lm）；如果r＜m，则出现多解。算法的伪代码如下：

算法 LNCBSD

输入 一个满足组播条件的网络拓扑图G=（V，E，S，R），其中，V表示顶点集合；E表示边集合；S是唯一的信源节点；R表示信宿节点集合

输出 边集合E中每条边ei的全局编码矢量g（ei）和局部编码矢量l（ei）

在上述算法中，原图用G=（V，E）表示，线图用LG=（LV，LE）表示，子树图用T=（TV，TE）表示。原图中的节点和边分别用ni和ei表示；线图和子树图中的节点和边分别加前缀l和t。此外，用|·|表示集合的基数。

4.2 算法示例

在本例中，算法的输入是如图2所示的单源组播网络。其中，节点S为信源，J，H，I分别为3个接收节点R1，R2，R3，S向3个接收节点组播传输2个符号σ1，σ2∈GF（2）。不难验证，该网络满足组播条件，即S和每个接收节点之间的最小割都为2。

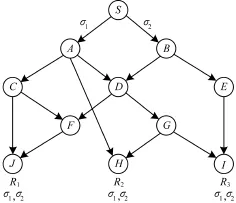
图2 示例网络

应用LNCBSD算法，具体步骤如下：

（1）生成与原图相对应的线图，如图3所示。

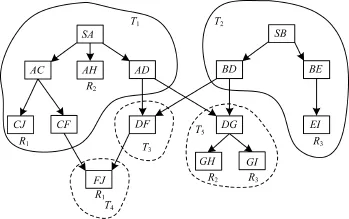
图3 图2所对应的线图

（2）基于线图生成子树图，如图4所示。

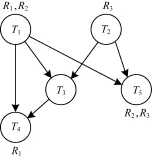
图4 图3化简后的子树图

（3）接收节点R1，R2，R3分配静态子树集，结果为：SR1=｛T1，T2T3T4｝，SR2=｛T1，T2T5｝，SR3=｛T1T5，T2｝，即表明，源节点S通过子树T1向接收节点R1传输符号σ1，通过子树T2T3T4向接收节点R1传输符号σ2。S通过子树T1向接收节点R2传输符号σ1，通过子树T2T5向接收节点R2传输符号σ2。S通过子树T1T5向接收节点R3传输符号σ1，通过子树T2向接收节点R3传输符号σ2。

（4）动态地生成各个子树的全局编码矢量。其中，由于图3中子树T1和T2内部流动的符号分别是σ1和σ2，因此自然得到T1子树的全局编码核g（T1）=（1 0），T2子树的全局编码核g（T2）=（0 1）。动态子树集和子树T3，T4，T5的全局编码核的分配如表1所示。其中，分配g（T5）时要兼顾与g（T1）和g（T2）的线性无关性，因此，分配成g（T5）=（1 1）。另外，由于子树内部的所有节点（原图中的边）和该子树使用相同的全局编码矢量，因此自然地得到原图所有边的全局编码矢量。本例中，以子树T5为例，原图中边DG，GH，GI的全局编码矢量都是（1 1）。

表1 全局编码核的动态分配表

（5）假设线图中编码节点DF，DG，FJ的局部编码矢量分别为l（DF）=（l1l2），l（DG）=（l3l4），l（FJ）=（l5l6），则应用式（5）可得：

写成向量的形式分别为：

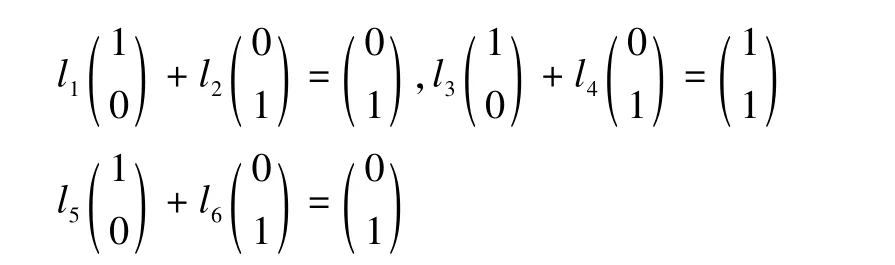
解得l（DF）=（0 1），l（DG）=（1 1），l（FJ）=（0 1）。

经过上述编码过程，接收节点J的2条入边收到的2个符号分别是σ1和σ2；接收节点H的2条入边收到的2个符号分别是σ1和σ1⊕σ2；接收节点I的2条入边收到的2个符号分别是σ1⊕σ2和σ2。经过模2运算后，在H和I也可以恢复出σ1和σ2，实现了组播的功能。

4.3 算法分析

应用LNCBSD算法伪代码中的符号，为了把原图转化为线图，需要扫描原图的全部边并建立邻接表，因此，其时间复杂度为O（|E|2）。由线图生成子树图的过程中，广度优先搜索的复杂度为O（|LV|+ |LE|），所以生成子树节点的复杂度为O（|LE||LV|+ |LE|2），拓扑排序的复杂度为O（|LV|+|LE|）。考虑到|LV|=|E|，且有|LE|=Θ（|E|），因此，生成子树图的复杂度为O（|E|2）。在子树图T中，为了给每个接收节点Ri建立静态子树集，需要在源节点S所位于的h个子树和接收节点Ri所位于的h个子树之间一一对应地建立h条路径，其时间复杂度为O（h|TE|）。进一步，由于存在着|R|个接收节点，因此建立静态子树集的时间复杂度为O（h|TE||R|）。分配全局网络编码矢量g（tni）时，需要检测h个h维向量的线性无关性，其复杂度为O（h2），所以为所有子树分配全局网络编码矢量的复杂度为O（h2|TE||R|）。应用式（5）计算局部编码矢量的复杂度为O（|TV|3）。

从译码的角度看，在每个接收节点处应用式（3）求解符号σ1，σ2，…，σh的复杂度是O（h2）。对大多数实际网络，经过子树分解后，子树图的节点数和边数都远小于原始网络的节点数和边数，即|TV|＜＜|V|，|TE|＜＜|E|，所以，问题的规模和编码复杂度大大降低。

4.4 仿真实验

本节基于Matlab设计了一组仿真实验对LNCBSD算法和文献［10］提出的多项式时间算法的效率做比较。首先，作为算法的输入，随机生成一个由n个节点（标号为1～n）构成的有向无环网络。为了防止环路的产生，网络中有向边都是由低序号节点指向高序号节点。2个节点之间的有向边按照概率p=0.7生成。另外，节点1充当源节点，再选取满足组播条件的2个接收节点。其次，在生成的网络中执行2种算法。为了比较算法的复杂度，对每次仿真读取原图和子树图的节点数和边数进行比较，并统计2种算法的运行时间，结果如图5～图7所示。可见，子树分解缩减了编码问题的规模和算法的运行时间，本文算法是一种高效的网络编码算法。

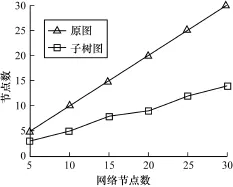
图5 原图和子树图的节点数比较

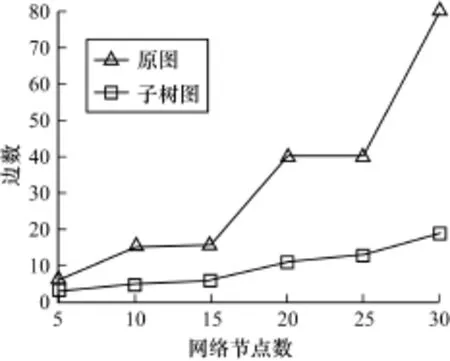
图6 原图和子树图的边数比较

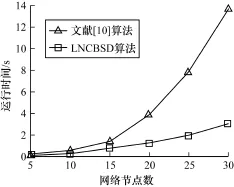
图7 LNCBSD和文献［10］算法的运行时间比较

5 结束语

本文提出了一种基于子树分解的组播网络编码算法（LNCBSD），该算法可用于解决固定拓扑有线网络的单源组播网络编码问题。LNCBSD算法借助于线图变换和子树分解把原始网络变成了子树图，每棵子树始于源节点或编码节点，终于接收节点或另一个编码节点，在每棵子树内部流动着相同的符号，不需要进行编码。由于子树图的节点数和边数远小于原始网络的节点数和边数，因此子树分解大幅缩减了问题的规模和编码的复杂度。因为网络拓扑不变，所以算法只需要执行一次就可以获得各个边的全局编码矢量和局部编码矢量，在随后的数据组播过程中，接收节点只需要解析发送符号即可，不需要重复分配和计算编码矢量。

LNCBSD算法是一种确定性算法，必须在拓扑已知的条件下有效，因此，不适用于如Ad Hoc这种拓扑可变的无线移动网络。另外，算法还有一些不完善的地方和不适用的场合。这是下一步的研究方向，具体包括：（1）算法不适用于无向图网络和拓扑未知网络，这需要用到诸如随机网络编码等的分布式编码方法。（2）算法没有考虑传输延时造成的符号不同步接收问题，这可以通过对发送符号进行分组来解决。（3）算法对单源组播应用有效。对于多源组播应用，可以通过增加虚拟源节点和虚拟边的方法转换成单源组播问题。但对于其他任意的应用场景，比如多重单播、多源任意播等应用，则可能要用到矢量编码甚至非线性编码［8］。此外，针对实际应用中有环网络、非单位容量边以及链路失效等问题，还需要对本文算法进行改进。

［1］ Fragouli C，Soljanin E.Network Coding Fundamentals［J］. Foundations and Trends in Networking，2007，2（1）：33-42.

［2］ Yeung RW.信息论与网络编码［M］.蔡 宁，译.北京：高等教育出版社，2011：411-483.

［3］ Koetter R，Medard M.An A lgebraic Approach to Network Coding［J］.IEEE/ACM Transactions on Network，2003，11（5）：782-795.

［4］ Cannons J，Dougherty R，Freiling C，et al.Network Routing Capacity［J］.IEEE Transactions on Information Theory，2006，52（3）：777-788.

［5］ Dougherty R，Freiling C，Zeger K.Unachievability of Network Coding Capacity［J］.IEEE Transactions on Information Theory，2006，52（6）：2365-2372.

［6］ Chekuri C，Fragouli C，Soljanin E.On Average Throughput and Alphabet Size in Network Coding［J］. IEEE Transactions on Information Theory，2006，52（6）：2410-2424.

［7］ Li S Y，Sun Q，Shao Z，et al.Linear Network Coding：Theory and Algorithm s［J］.Proceedings of the IEEE，2011，99（3）：372-387.

［8］ Dougherty R，Freiling C，Zeger K.Insufficiency of Linear Coding in Network Information Flow［J］.IEEE Transactions on Information Theory，2005，51（8）：2745-2759.

［9］ Kotter R，Kschischang F R.Coding for Errors and Erasures in Random Network Coding［J］.IEEE Transactions on Information Theory，2008，54（8）：3579-3591.

［10］ Ho T，Medard M，Koetter R，et al.A Random Linear Network Coding Approach to Multicast［J］.IEEE Transactions on Information Theory，2006，52（10）：4413-4430.

［11］ Jaggi S，Sanders P，Chou P A，et al.Polynom ial Time Algorithms for Multicast Network Code Construction［J］. IEEE Transactions on Information Theory，2005，51（6）：1973-1982.

［12］ Ebrahim i JB，Fragouli C.A lgebraic Algorithm for Vector Network Coding［J］.IEEE Transactions on Information Theory，2011，57（2）：996-1007.

［13］ Bassoli R，Marques H，Rodriguez J，et al.Network Coding Theory：A Survey［J］.IEEE Communications Surveys&Tutorials，2013，15（4）：1950-1978.

［14］ Ahlswede R，Cai N，Li S Y，et al.Network Information Flow［J］.IEEE Transactions on Information Theory，2000，46（4）：1204-1216.

［15］ Buckley F，Lew inter M.图论简明教程［M］.李慧霸，王凤芹，译.北京：清华大学出版社，2005：69-70.

［16］ Harvey N JA，Karger D R，Murota K.Deterministic Network Coding by Matrix Completion［C］//Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithm.New York，USA：ACM Press，2005：489-498.

［17］ Fragouli C，Soljanin E.Information Flow Decomposition for Network Coding［J］.IEEE Transactions on Information Theory，2004，52（3）：829-848.

［18］ Montanari A，Urbanke R L.Iterative Coding for Network Coding［J］.IEEE Transactions on Information Theory，2013，59（3）：1563-1572.

［19］ Lien C，Chang C，Lee D.A Universal Stabilization Algorithm for Multicast Flows with Network Coding［J］. IEEE Transactions on Communications，2013，61（2）：712-721.

［20］ Marden JR，Effros M.The Price of Selfishness in Network Coding［J］.IEEE Transactions on Information Theory，2012，58（4）：2349-2361.

［21］ 文瑞涵，冯 钢.基于网络编码的多跳无线网络可靠组播［J］.电子与信息学报，2012，34（11）：2721-2727.

［22］ 屈毓锛，陈 晨，董 超，等.基于Markov状态转移方法的网络编码时延分析［J］.通信学报，2013，34（9）：77-83.

［23］ 郭网媚，李 娜，王 骁.序列矩阵表示的卷积网络编码的译码方法［J］.吉林大学学报，2013，43（4）：1076-1081.

［24］ Ahuja R K，Magnanti R L，Orlin JB.Network Flows［M］. Englewood Cliffs，USA：Prentice Hall，1993：77-79.

编辑 金胡考

A Multicast Linear Network Coding Algorithm Based on Subtree Decomposition

LIU Yantao，XIA Guiyang，XU Jing，QIN Na
（College of Engineering，Bohai University，Jinzhou 121000，China）

Aiming at network coding for single source multicast networks w th fixed topology，this paper proposes a Linear Network Coding（LNC）algorithm based on subtree decomposition.It is com posed of five steps：line graph transforming，subtree decomposition，edge disjoint path search，global coding vector assignment and local coding vector calculation.The algorithm starts with input of a Directed Acyclic Graph（DAG）with multicast property，and ends with output of global coding vectors and local coding vectors of each edge.Subtree decomposition is based on such a consideration that there is no need of coding within a subtree but only between subtrees.It is proved by theoretical analyses and experimental results show that，both network scale and complexity of path search and coding are greatly decreased through subtree decomposition，which greatly decreases running time of network coding algorithm.It can draw the conclusion that the proposed algorithm is an efficient algorithm to single source multicast networks.

Linear Network Coding（LNC）；Directed Acyclic Graph（DAG）；line graph；subtree decomposition；coding vector

刘宴涛，夏桂阳，徐 静，等.一种基于子树分解的组播线性网络编码算法［J］.计算机工程，2015，41（11）：153-159.

英文引用格式：Liu Yantao，Xia Guiyang，Xu Jing，et al.A Multicast Linear Network Coding Algorithm Based on Subtree Decomposition［J］.Computer Engineering，2015，41（11）：153-159.

1000-3428（2015）11-0153-07

A

TN915

10.3969/j.issn.1000-3428.2015.11.027

国家自然科学基金资助项目（61101129，61227001）；山东省航天创新基金资助项目（2014JJ005）。

刘宴涛（1975-），男，副教授、博士，主研方向：Ad Hoc网络，网络编码，网络仿真；夏桂阳、徐 静、秦 娜，硕士研究生。

2014-08-18

2014-12-24 E-m ail：liuyantaocn@163.com