基于相对变化分析的多模态卷烟制叶丝段故障监测

王 伟，赵春晖，楼卫东，张利宏

1.浙江中烟工业有限责任公司，杭州市西湖区科海路118号 310024

2.浙江大学控制科学与工程学系 工业控制技术国家重点实验室，杭州市西湖区浙大路38号 310027

基于相对变化分析的多模态卷烟制叶丝段故障监测

王 伟1,2，赵春晖2，楼卫东1，张利宏1

1.浙江中烟工业有限责任公司，杭州市西湖区科海路118号 310024

2.浙江大学控制科学与工程学系 工业控制技术国家重点实验室，杭州市西湖区浙大路38号 310027

为解决卷烟制叶丝段中采用传统单变量统计过程控制方法故障监测效果欠佳等问题，通过对制叶丝段关键设备的运行特性分析，提出了一种基于相对变化分析的故障监测方法。该方法采用属性展开方式将具有批次、时间和属性特点的三维数据展开成二维数据，采用主元分析方法进行参考模态的统计建模和故障监测，根据备选模态的潜在过程波动以及与参考模态的相对变化，将参考模态监测模型的主元子空间和残差子空间分别进行分解，在分解后的4个子空间中进行备选模态的统计建模和故障监测。基于设备实际运行数据进行离线验证，结果表明：与彩虹图、过程能力指数等传统故障监测方法相比，该方法能更深入地揭示不同模态、不同批次间的过程变量动态性以及变量间关联关系的变化，可以及时、有效地检测出设备故障。

卷烟；制叶丝段；多批次；多模态；主元分析；建模；子空间分解；故障监测

随着我国烟草行业整体实力的不断提高，有效提升设备的智能化水平和高效运行能力已成为卷烟工业企业关注的焦点，而设备故障监测是保证设备智能化和高效运行的重要手段。目前针对卷烟制叶丝段，主要以连续过程单变量统计过程控制方法为基础［1-10］，利用彩虹图和过程能力指数对关键设备的可直接测量并用单变量描述的故障进行监测。但上述研究主要是对某一产品牌号同一批次内的过程特性进行分析，仅局限于单一时间轴的研究，缺少对批次轴上动态信息的有效分析，这种局限于批次内对单个过程变量进行独立监测的方法，无法及时反映过程变量的动态性以及变量间关联关系的变化，同时也未充分考虑由于生产策略以及运行条件的调整而产生的多模态特性。以主元分析（Principal Component Analysis，PCA）为代表的多元统计分析方法，可以从海量数据中提取出高质量信息进行设备状态的综合统计监测，在石油化工、钢铁制造、有色冶金、火力发电、注塑封装、半导体生产等工业过程监测领域得到了广泛应用［11-12］。多元统计分析方法在烟草行业的应用及相关研究主要集中在卷烟感官质量和化学成分等方面的监测［13-15］，在卷烟生产设备的故障监测领域尚未见报道。近年来，应用多元统计分析方法针对多模态过程的故障监测得到了越来越多的关注［16-21］，主要采用多模型思想对不同模型分别建立监测模型，进而形成包含全部模态的模型库，并根据当前数据在模型库中选取匹配度最高的模型进行在线监测。为此，借鉴多模态间歇过程［22-23］的已有研究成果，通过分析卷烟制叶丝段关键设备运行过程的多批次、多模态特性，提出一种基于相对变化分析的故障监测方法，并根据设备实际运行数据离线验证该方法的有效性，以期为提高卷烟制叶丝段设备故障监测的可靠性和准确性提供理论支撑。

1 过程变量选取与数据处理

1.1 过程变量选取

卷烟制丝过程属于典型的流程制造批次过程，既具有批量产品生产的特点，又具有多个生产批次、产品频繁变化的特点。卷烟制丝过程主要由片烟预处理段、制叶丝段和掺配加香段3个工艺段组成，其中制叶丝段是将片烟制成合格的叶丝。杭州卷烟厂制叶丝段的关键设备有德国Hauni公司的Sirox增温增湿和KLD薄板烘丝设备，包含有23个过程变量，见表1。

表1 杭州卷烟厂制叶丝段的过程变量

1.2 三维数据处理

针对“利群（软长嘴）”叶丝牌号的一个生产批次操作过程具有Ki个采样点和J个测量变量，则该生产批次可以得到一个二维数据矩阵，对该产品牌号重复I个生产批次后，获得的原始数据可以表述为一个三维数据矩阵X（I×J×Ki）。

杭州卷烟厂制丝管理系统中的过程变量每10 s采样一次，为克服测量噪声的影响并与制丝管理系统彩虹图监测数据的频率保持一致，采用平滑滤波方法对连续6个采样数据做算数平均以得到一个有效数据，获得三维过程变量数据矩阵X（I×J×Ki）。由于每个生产批次操作时间不确定造成批次间的采样数据不等长，第i个批次的样本点为 Ki，见图 1。

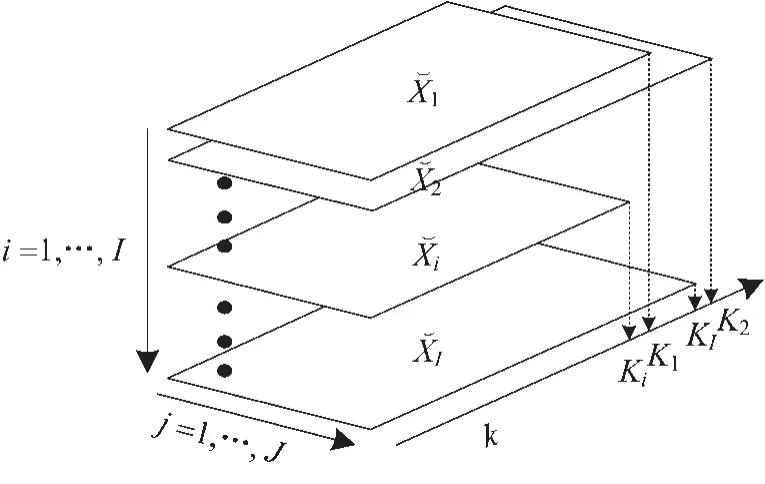
图1 卷烟制叶丝段的三维不等长数据

通过对制叶丝段设备运行数据的分析发现，同一批次内只存在一个稳定工况，说明变量间的相互关系具有相同的过程特征，同时考虑数据不等长特点，采用属性展开方式将三维矩阵X（I×J×Ki）展开成二维矩阵X（IKi× J），见图2。

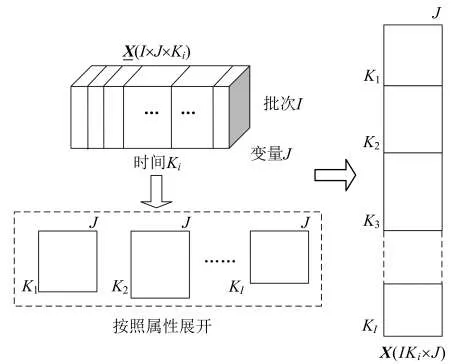
图2 按照属性展开后的二维数据分析单元

设二维矩阵X（I Ki×J）内任意一点的变量为xik，j，对该变量进行减均值、除标准差等标准化预处理。标准化后的数据突出过程变量测量值在时间方向上的变化，由于同一批次内只存在一个稳定工况，因此该均值和方差代表了过程运行的平均水平和波动程度。标准化处理的计算公式为：

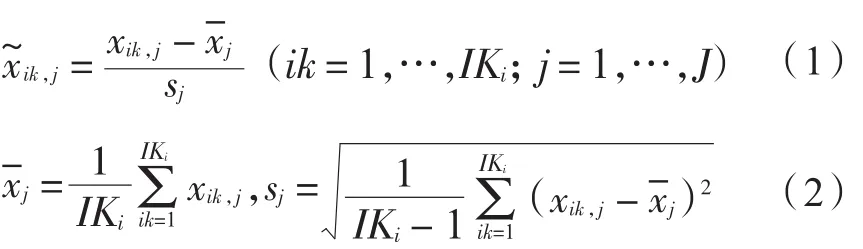
2 统计监测模型与故障在线监测

PCA方法要求用来建模的正常过程数据必须来自于单一的生产操作范围（即一个稳定的运行模态），对于某一产品牌号的一个生产批次而言，除去料头和料尾的干扰，在物料的整个中间处理过程只存在一个稳定的运行模态，可以利用PCA方法通过三维数据的属性展开进行统计建模和在线监测。然而，由于生产策略以及运行条件的调整，在相同产品牌号的不同批次间会存在不同的稳定工作点，表现为正常过程数据的均值、方差、相关关系等特征变量会有明显的变化，即不同批次间具有多个稳定的运行模态，无法直接采用PCA方法对多个稳定运行模态进行统计建模和在线监测。因此，本研究中根据备选模态的潜在过程波动以及与参考模态的相对变化，采用面向多模态间歇过程的子空间分解方法进行统计建模和在线监测。

2.1 参考模态的统计监测模型

通过对现场生产策略以及运行条件的收集整理，将制叶丝段设备的一个稳定运行模态作为参考模态，采集该模态下“利群（软长嘴）”叶丝牌号不同批次的设备运行数据，通过数据处理获得参考模态建模数据矩阵Xr（IrKir×J）。将其进行PCA分解，PCA分解的计算公式为：

式中：Tr为主元子空间中（IrKir× Rr）维的得分矩阵；Pr为主元子空间中（J× Rr）维的负载矩阵；Er为残差子空间中（IrKir×J）维的残差矩阵为残差子空间中维的负载矩阵，R表示主元个

r数，由累计贡献率确定

设λ1，λ2，…，λJ为建模数据集Xr的协方差矩阵的全部特征值，保留原始数据空间中90%以上的波动信息，则由累计贡献率方法确定主元个数Rr的计算公式为：

2.2 参考模态监测模型的控制限

基于参考模态建模数据，离线计算主成分子空间的Hotelling-T2和残差子空间的SPE（Squared Prediction Error）统计量。Tr2监测统计量的计算公式为：

式中：tr，ik＝xr，ikPr为（1× Rr）维的主元得分向量，xr，ik为建模数据 Xr的第 ik 行；对角矩阵 Sr＝diag（λ1，…，λRr）由建模数据 Xr的协方差矩阵的前Rr个特征值所构成。

SPEr监测统计量的计算公式为：

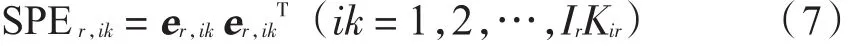
式中：er，ik表示xr，ik与重构的偏差向量，xr，ik＝表示重构得到的（1× J）维估计向量。

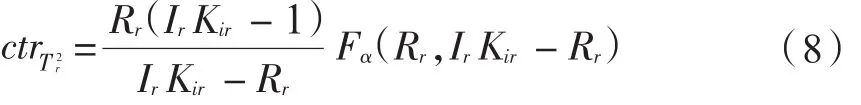
式中：Rr为保留的主元个数；IrKir为样本数；α为置信度，Fα（Rr，IrKir－Rr）是对应于置信度为α，自由度为Rr，IrKir－Rr条件下的F分布临界值。

根据χ2分布计算SPEr监测统计量的控制限ctrSPEr为：

式中：var(·)为围绕参考模态中心的波动方差。

如果Ratioa，r（i）＞1，表明备选模态中第i个方向上的波动大于参考模态该方向上的波动。Ratioa，r中大于1的方向所包含的波动是导致备选模态数据下，参考模态PCA监测模型监测统计量超限的原因。选取Ratioa，r中大于1的方向所对应的Pr的列，构成中剩余的列构成显然

式中：g＝v/2n，h＝2n2/v，n、v分别为 SPEr监测统计量的均值和方差。

2.3 备选模态的统计监测模型

2.3.1 主元子空间分解和统计建模

将与参考模态不同的另一种稳定运行模态作为备选模态，采集该模态下“利群（软长嘴）”叶丝牌号不同批次的设备运行数据，通过数据处理获得备选模态建模数据矩阵Xa（IaKia×J）。将其在Pr方向上进行投影，获得参考模态的主元得分Ta：

为表征主元子空间中备选模态和参考模态波动的比值，引入 Rr维的 Ratioa，r指标：

台肇地区部分注水管线使用年限较长，管壁结垢、腐蚀严重，注水压力损失较大，增加了无效的能耗，加之部分老化的复合管，出现穿孔、渗漏、损坏等现象[3]，对注水系统效率产生负面影响。

式中：（J×Ra，f）维负载矩阵 Pa，f和（J×Ra，0）维负载矩阵 Pa，0的主元个数分别为且

2.3.2 残差子空间分解和统计建模

将建模数据Xa在方向上进行投影，获得参考模态残差子空间中的波动Ea：

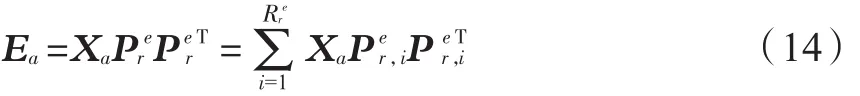
式中：·2表示欧式距离。

如果Δa，r（i）＞0，表明备选模态中第i个方向上的波动大于参考模态该方向上的波动。Δa，r中大于零的方向所包含的波动是导致在备选模态数据下，参考模态PCA监测模型SPEr监测统计量超限的原因。选取Δa，r中大于零的方向所对应的的列，构成中剩余的列构成显然

最终的残差计算公式为：

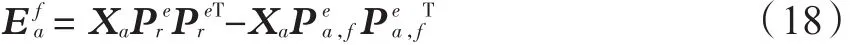
2.4 备选模态监测模型的控制限

基于备选模态建模数据，离线计算备选模态下4个监测模型Tf2、Tn2、Te2、SPEf监测统计量：

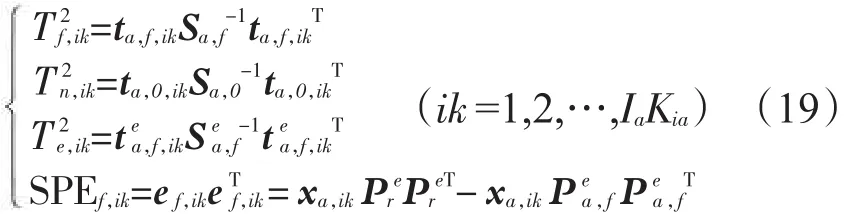
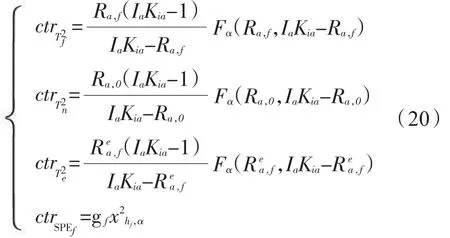
式中：α为置信度，Fα（·）为对应于置信度为α的 F分布临界值分别为SPEf统计量的均值和方差。

2.5 基于统计监测模型的故障在线监测

在线监测时，利用参考模态建模数据的均值和标准差对有效数据进行标准化处理，获得xr，new（1×J）。采用参考模态监测模型计算T2r，new和SPEr，new监测指标：

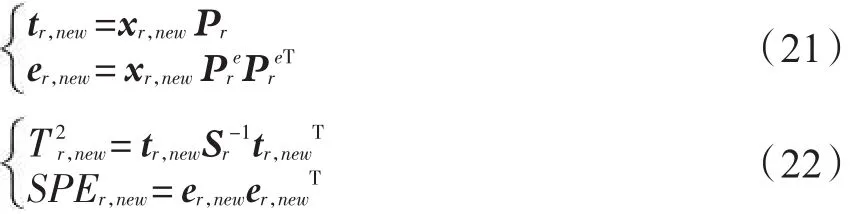
式中：Pr和Pre分别为参考模态主元子空间和残差子空间的负载矩阵；对角矩阵Sr由建模数据集Xr的协方差矩阵的前Rr个特征值所构成。

如果两个监测统计量都位于控制限内，表明制叶丝段处于参考模态的正常状态，如果其中至少一个监测统计量超出控制限，则需利用备选模态监测模型进行进一步分析。

利用备选模态建模数据的均值和标准差对有效数据进行标准化处理，获得 xa，new（1×J）。采用备选模态监测模型计算监测指标：

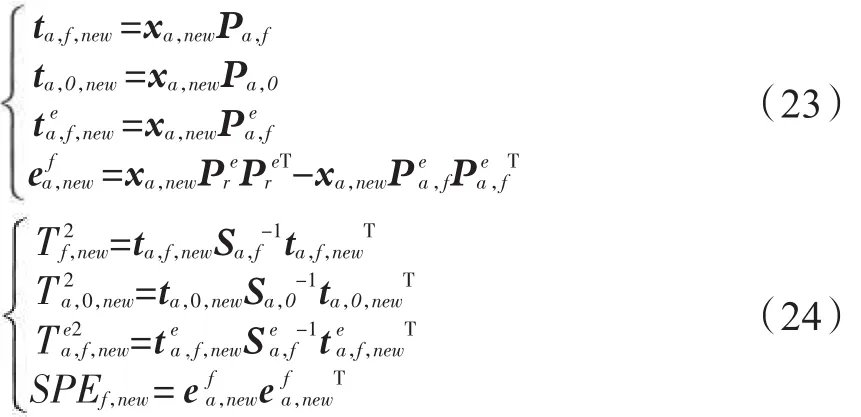
如果4个监测统计量都位于相应控制限内，表明制叶丝段处于备选模态的正常状态，如果其中至少一个监测统计量超出控制限，则表明制叶丝段发生故障。

3 数据验证与结果分析

选取杭州卷烟厂2014年6月—2015年4月制叶丝段C线“利群（软长嘴）”叶丝牌号的设备运行数据进行监测模型的离线验证，实验使用Matlab 2011b软件，算法通过编写m文件实现。

3.1 参考模态监测模型的效果验证

选取“利群（软长嘴）”叶丝牌号参考模态下28个正常批次运行数据作为原始建模数据，通过数据处理获得参考模态的二维建模数据矩阵Xr（2 677×23）。采用主元分析法建立参考模态统计监测模型，确定主元个数为10（即Rr=10），则Pr为（23×10）维负载矩阵；，则维负载矩阵。控制限的置信度选取为0.99，T2统计量的控制限ctrT2为23.36，SPE统计量的控制限ctrSPE为8.42。

选取参考模态下10个正常批次运行数据作为原始测试数据，通过数据处理获得二维测试数据矩阵Xr（1 077×23），使用参考模态监测模型对参考模态测试数据在线监测，结果见图3。为进行比较，重新选取2个参考模态下正常批次的运行数据并进行数据处理，在第41个样本点时，令1区筒壁温度的值跃性增长10%，一直持续到第100个样本点时恢复正常，使用参考模态监测模型对参考模态故障数据在线监测，结果见图4。

引入首次故障报警时间，定义为连续10个监测统计量超过对应控制限的采样时间点。由图3可知，在两个监测子空间中有个别时刻的监测统计量超出控制限，主要为生产过程中的随机干扰所致。根据首次故障报警的定义，两个监测统计量和SPEr都未发生故障报警，表明参考模态监测模型具有准确监测参考模态正常批次的能力。由图4可知，当1区筒壁温度故障时，在第50个采样时刻检测出首次故障报警，表明参考模态监测模型具有准确监测参考模态故障批次的能力。

3.2 备选模态监测模型的效果验证

选取备选模态下7个正常批次运行数据作为原始测试数据，通过数据处理获得二维测试数据矩阵Xr（711×23），使用参考模态监测模型对备选模态测试数据在线监测，结果见图5。由图5可知，两个监测统计量和SPEr在第10个采样时刻均发生首次故障报警，通过现场排查，引起故障的原因是由于生产策略以及运行条件调整，属于与参考模态不同的另一个稳定运行模态。为避免产生误报警，需要构建备选模态监测模型，并在参考模态监测模型的监测统计量超限时，利用备选模态监测模型做进一步判断。

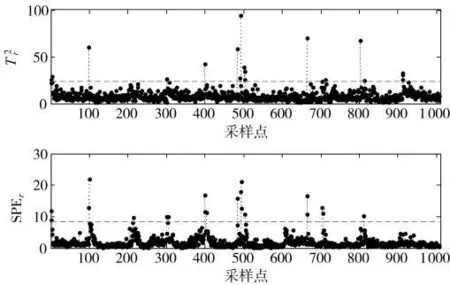
图3 使用参考模态监测模型对参考模态测试数据的监测结果

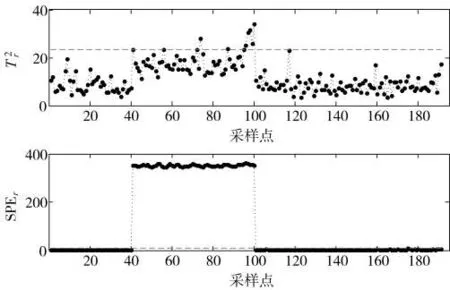
图4 使用参考模态监测模型对参考模态故障数据的监测结果

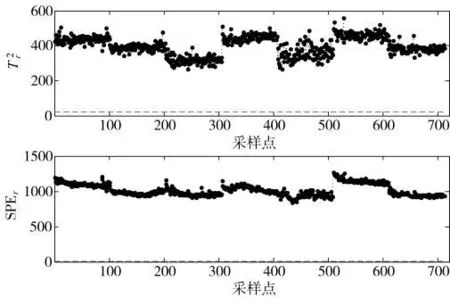
图5 使用参考模态监测模型对备选模态测试数据的监测结果

选取“利群（软长嘴）”叶丝牌号备选模态下另外7个正常批次运行数据作为原始建模数据，通过数据处理获得备选模态的二维建模数据矩阵Xa（702×23）。采用相对变化分析对参考模态监测模型的主元子空间进行分解获得 Pa，f和 Pa，0子空间，通过指标 Ratioa，r的计算可以将 Rr分解为 R*a和两部分，计算得到，则维矩阵；，则为（23×4）维矩阵。Pa，f和 Pa，0子空间中主元个数分别为 Ra，f=6、Ra，0=1，对应的负载矩阵Pa，f为（23×6）维矩阵、Pa，0为（23×1）维矩阵。采用相对变化分析对参考模态监测模型的残差子空间进行分解获得子空间和残差子空间，通过指标Δa，r的计算可以将分解为和两部分，计算得到则维矩阵；则为（23×8）维矩阵。子空间中主元分数为对应的负载矩阵为（23×4）维矩阵。控制限的置信度选取为 0.99，SPEf监测统计量的控制限分别为 ctrT2f=17.11、ctrT2n=13.46、ctrT2e=6.68、ctrSPEf=16.24。选取图5中使用的备选模态下7个正常批次运行数据作为原始测试数据，通过数据处理获得二维测试数据矩阵Xa（711×23），使用备选模态监测模型对备选模态测试数据进行监测，结果见图6。

由图6可知，在4个监测子空间中有个别时刻的监测统计量超出控制限，同样为生产过程中的随机干扰所致。根据首次故障报警的定义，4个监测统计量都未发生故障报警，表明备选模态监测模型具有准确监测备选模态正常批次的能力。

基于备选模态测试数据Xa（711×23），在备选模态监测模型Pea，f子空间中引入指数形式的扰动K（1-e-t/τ），扰动参数为 K=5，τ=200，扰动从第 151个采样点开始，至第550个采样点结束。为进行比较，基于备选模态建模数据 Xa（702×23），采用主元分析法建立备选模态的传统PCA监测模型，使用备选模态监测模型和传统PCA监测模型进行监测，结果见图7和图8。

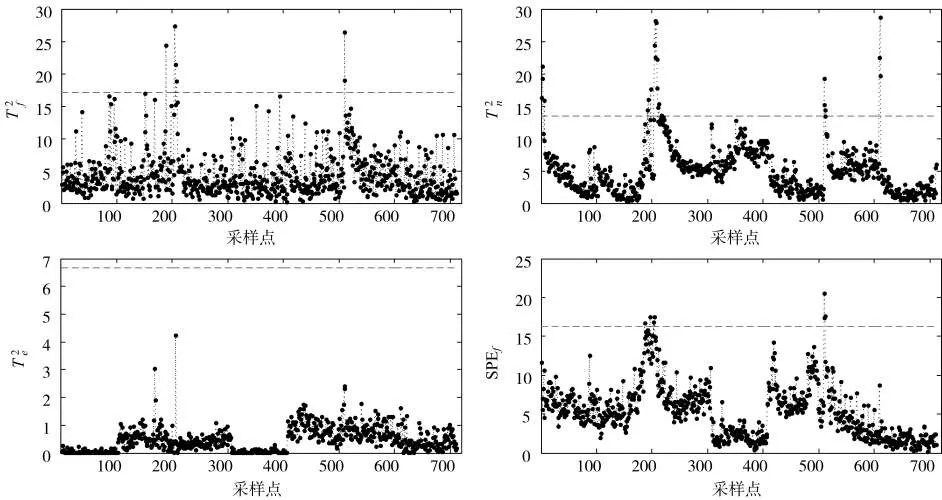
图6 使用备选模态监测模型对备选模态测试数据的监测结果

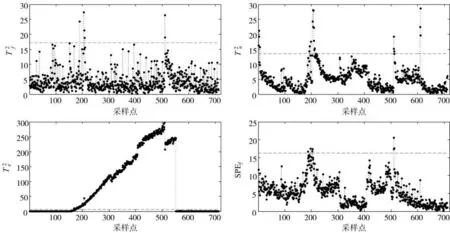
图7 子空间添加扰动后使用备选模态监测模型的监测结果

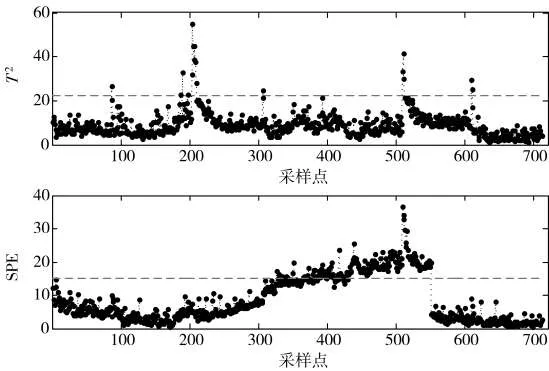
图8 子空间添加扰动后使用传统PCA监测模型的监测结果

由图7和图8可知，备选模态监测模型和传统PCA监测模型均可以监测到故障发生。其中，备选模态监测模型的监测统计量T2e超过控制限，首次故障报警发生在第181个采样点；传统PCA监测模型的监测统计量SPE超过控制限，首次故障报警发生在第395个采样点。可见，与传统PCA监测模型相比，备选模态监测模型能够更早检测出故障发生。

4 结论

本研究中将面向多模态间歇过程的三维数据分析和子空间分解方法引入卷烟制叶丝段故障监测中，通过对制叶丝段关键设备的运行特性分析，将设备的一个稳定运行模态作为参考模态，采用三维数据属性展开和PCA方法进行参考模态主元子空间和残差子空间的统计建模和在线监测。将与参考模态不同的另一个稳定运行模态作为备选模态，定义 Radioa，r和Δa，r两个衡量指标深入分析不同模态各个监测方向上的过程特性变化，基于不同模态间的相对变化分别对参考模态的主元子空间和残差子空间进行分解，在获得的4个子空间中分别进行基于PCA方法的统计建模和故障监测。相比彩虹图、过程能力指数等传统故障监测方法，本文中所提出的方法能够更深入地揭示不同模态、不同批次间的过程变量动态性以及变量间关联关系的变化，基于设备实际运行数据的离线验证表明，该方法能够更灵敏、更有效地检测出设备故障。

［1］ 李攀，张家毅，程哲，等.卷烟企业自动控制技术的发展趋势［J］.烟草科技，2002（2）：21-24.

［2］ 张敏，童亿刚，戴志渊，等.SPC技术在制丝质量管理中的初步应用［J］.烟草科技，2004（9）：10-11.

［3］ 黄胜，李建辉，张永川.长沙卷烟厂SPC系统的应用实践［J］.中国烟草学报，2008，14（S1）：14-17.

［4］ Mishra B，Dangayach G S.Performance improvement through statistical process control：a longitudinal study［J］.International Journal of Globalization and Small Business，2009，3（1）：55-72.

［5］ 李文泉，赵文田，李文斌.统计过程控制技术SPC在烟草制丝生产中的应用［J］.机械工程与自动化，2009（5）：116-118.

［6］ 罗江，刘强斌.SPC系统在卷烟工业企业质量管理中的应用实践［J］.产业经济，2011（3）：67-72.

［7］ 纪盛强，程晶晶，李郡.基于SPC和神经网络的卷烟制丝生产质量监控方法研究［J］.工业控制计算机，2011，24（12）：65-68.

［8］ 李铁军，杨得强，李强.SPC系统在卷烟制丝工艺质量控制的应用［J］.中国质量，2013（4）：87-88.

［9］ 朱敏，王培琛，张学礼，等.基于统计过程控制的卷烟品控系统［J］.可编程控制器与工厂自动化，2014（3）：58-62.

［10］钱杰，徐进，季琦，等.制造执行系统在烟草企业中的应用［J］.机械制造与自动化，2014，43（2）：147-149.

［11］Wang H，Chai T Y，Ding J L，et al.Data driven fault diagnosis and fault tolerant control：some advances and possible new directions［J］.Acta Automatica Sinica，2009，35（6）：739-747.

［12］刘强，柴天佑，秦泗钊，等.基于数据和知识的工业过程监视及故障诊断综述［J］.控制与决策，2010，25（6）：801-807.

［13］杨锦忠，宋希云.多元统计分析及其在烟草学中的应用［J］.中国烟草学报，2014，20（5）：134-138.

［14］邵惠芳，赵昕宇，许自成，等.基于Fisher判别分析的烤烟感官质量与工业应用价值的关系研究［J］.中国烟草学报，2011，17（6）：13-18.

［15］李伟，冯洪涛，周桂圆，等.Hotelling T2结合多组分NIR校正模型在卷烟生产过程质量监测中的应用［J］.烟草科技，2014（7）：5-9.

［16］ Zhao S J，Zhang J，Xu Y M.Monitoring of processes with multiple operating modes through multiple principal component analysis models［J］.Industrial&Engineering Chemistry Research， 2004， 43（22）：7025-7035.

［17］Zhao S J，Zhang J，Xu Y M.Performance monitoring of processes with multiple operating modes through multiple PLS models［J］.Journal of Process Control，2006，16（7）：763-772.

［18］Lee Y H，Jin H D，Han C H.On-line process state classification for adaptive monitoring［J］.Industrial&Engineering Chemistry Research， 2006， 45（9）：3095-3107.

［19］Camacho J， Pico J. Online monitoring of batch processes using multi-phase principal component analysis［J］.Journalof Process Control， 2006，16（10）：1021-1035.

［20］Xie X，Shi H B.Dynamic multimode process modeling and monitoring using adaptive Gaussian mixture models［J］.Industrial and Engineering Chemistry Research，2012，51（15）：5497-5505.

［21］Zhang Y W， WangC， LuR Q.Modelingand monitoring of multimode process based on subspace separation［J］.ChemicalEngineering Research and Design，2013，91（5）：831-842.

［22］Zhao C H，Yao Y，Gao F R，et al.Statistical analysis and online monitoring for multimode processes with between-mode transitions ［J］.ChemicalEngineering Science.2010，65（22）：5961-5975.

［23］Zhao C H.Concurrent phase partition between-mode statistical analysis for multimode and multiphase batch process monitoring［J］.AICHE Journal，2014，60（2）：559-573.

Failure Monitoring of Multi-mode Tobacco Strip Processing Based on Relative Variation Analysis

WANG Wei1,2,ZHAO Chunhui2,LOU Weidong1,and ZHANG Lihong1
1.China Tobacco Zhejiang Industrial Co.,Ltd.,Hangzhou 310024,China
2.State Key Laboratory of Industrial Control Technology,Department of Control Science and Engineering,Zhejiang University,Hangzhou 310027,China

Not satisfied with the traditional monovariant statistical process control in tobacco strip processing,a failure monitoring approach based on relative variation analysis was proposed via analyzing the running characteristics of key processing equipments.The approach adopted attribution expansion to convert the three-dimensional data of batch,time and attribution characteristics into two-dimensional data and applied principal component analysis method to statistical modeling for failure monitoring under reference mode.According to the potential process fluctuation of alternate mode and its relative variation against the reference mode,the principal component subspace and residual subspace of monitoring model for reference mode were dissolved separately,then the statistical modeling for failure monitoring under alternate mode were carried out in the dissolved four subspaces.Off-line validation was conducted based on actual running data of equipments,the results showed that:comparing with traditional failure monitoring methods,such as pre-control diagram and process capability index,the proposed methodrevealed the dynamic variations of process variables and correlation between variables for different modes and batches in depth,and detected equipment failures timely and effectively.

Cigarette;Strip processing;Multi-batch;Multi-mode;Modeling;Principal component analysis Failure monitoring

TS432

A

1002-0861（2015）12-0078-09

10.16135/j.issn1002-0861.20151213

2015-06-26

2015-09-16

国家自然科学基金资助项目“批次过程监测与故障诊断的基础理论研究”(61422306)和“间歇过程高效运行的建模控制方法及应用”（61433005)。

王伟(1982—)，博士，工程师，主要从事复杂工业过程智能建模、运行优化和故障诊断研究。E-mail:wangwei-hy@zjtobacco.com

王伟，赵春晖，楼卫东，等.基于相对变化分析的多模态卷烟制叶丝段故障监测［J］.烟草科技，2015，48（12）：78-86.WANG Wei,ZHAO Chunhui,LOU Weidong,et al.Failure monitoring of multi-mode tobacco strip processing based on relative variation analysis［J］.Tobacco Science&Technology,2015,48（12）：78-86.

责任编辑 曹 娟