机床上下料机器人运动学分析与仿真

余伊薇

(湖北久之洋红外系统股份有限公司，湖北 武汉 430000)

机床上下料机器人运动学分析与仿真

余伊薇

(湖北久之洋红外系统股份有限公司，湖北 武汉 430000)

采用D-H坐标方法对机床上下料机器人运动学进行分析，获得了运动学正解和逆解。采用蒙特卡洛方法，运用MATLAB编程计算了其工作空间，然后在工作空间内对其运动路径进行了规划。将该路径的逆解数值在ADAMS中进行了虚拟样机仿真，获得的实验数据为上下料机器人结构设计和优化提供了很好的理论依据。

D-H坐标；机床上下料机器人；仿真；运动学

0 引言

机床上下料机器人适用于机床、生产线的自动上料/下料、工件移位翻转、工件转序等，主要针对圆盘类、长轴类、不规则形状、金属板类等工件，在工业自动化中得到广泛的应用。机器人的运动学性能一直是机器人设计研究的核心工作，它是空间轨迹规划和优化设计的基础。本文采用ADAMS仿真软件对其进行了运动学仿真，并验证了轨迹规划的正确性。

1 机器人结构

图1为机床上下料机器人物理样机图。从图1可以看出，本文设计的6自由度机床上下料机器人由底座、腰部、大臂、小臂、手腕及手部等6部分组成，每个关节均为旋转关节且安装安川伺服电机，通过6轴联动使机器人末端点完成规定的轨迹路径运动，从而实现机床的上下料功能。该6自由度机器人在工作空间的活动范围内能达到任意的位置，其结构紧凑，体积精小，动作灵活，适用于机床的上下料作业。

图1 机床上下料机器人物理样机

2 机床上下料机器人的运动学正解和逆解

本文采用D-H[1]法建立机器人末端坐标系到基座坐标系之间的齐次变换矩阵，通过一个4阶的齐次变换矩阵来描述连杆相对机身的位姿，依次通过这种齐次变换矩阵建立机床上下料机器人的运动学方程，进而求得其运动学正解和逆解，同时它们也是运动学研究的重点。

2.1 运动学正解

采用小端法建立机床上下料机器人的D-H坐标系，如图2所示，其D-H参数如表1所示。

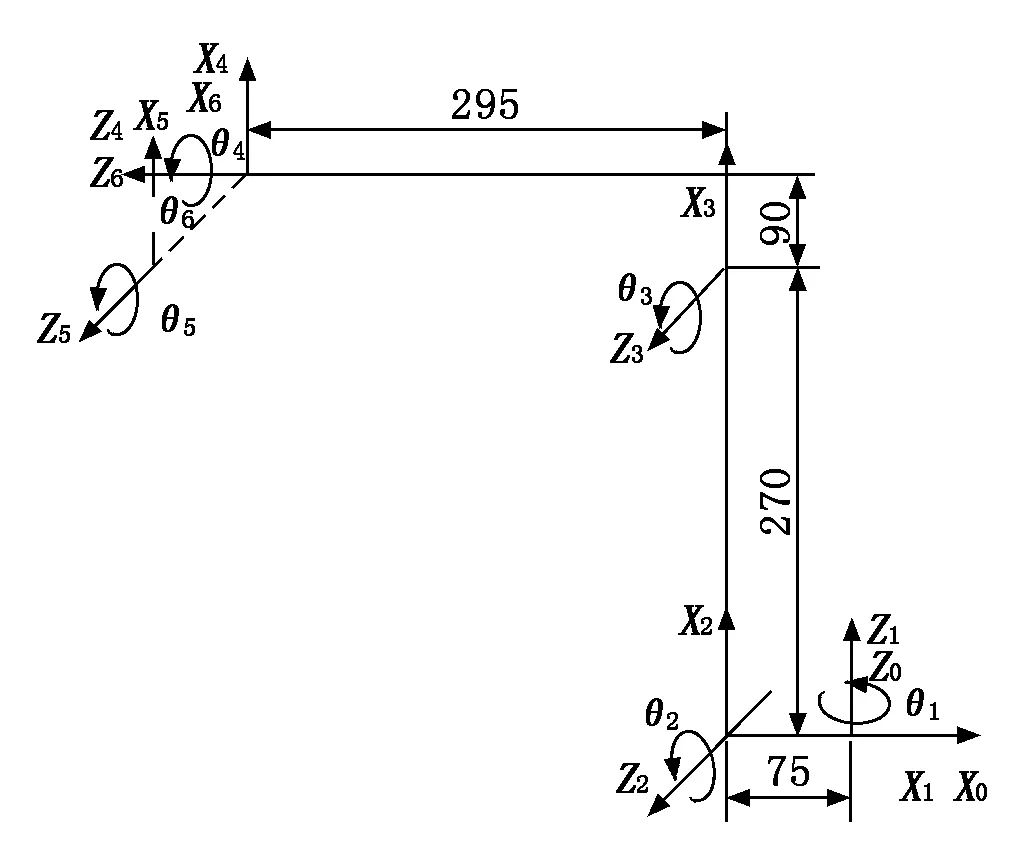
图2 机床上下料机器人D-H坐标系

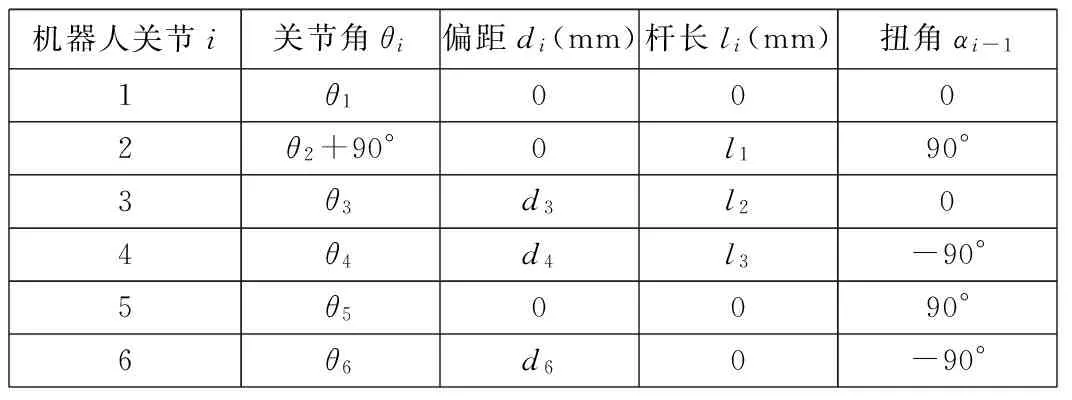
机器人关节i关节角θi偏距di(mm)杆长li(mm)扭角αi-11θ10002θ2+90°0l190°3θ3d3l204θ4d4l3-90°5θ50090°6θ6d60-90°

(1)

其中：s=sin；c=cos。

将表1中的D-H参数代入式(1)中，可求得相邻连杆之间的变换矩阵，将其依次相乘，就可得到机床上下料机器人末端执行器相对于机身坐标系的变换矩阵为：

(2)

2.2 运动学逆解

先将机床上下料机器人的运动方程写为：

(3)

其中：nx、ny、nz为法向矢量n在固定坐标系3个坐标轴方向的分量；ox、oy、oz为姿态矢量o在固定坐标系3个坐标轴方向的分量；ax、ay、az为接近矢量a在固定坐标系3个坐标轴方向的分量；px、py、pz为在固定坐标系中的位置坐标。

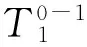
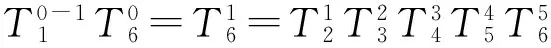
(4)

根据等式(4)中的两边矩阵中第二行第四列元素对应相等可得：

-s1(px-d6ax)+c1(py-d6ay)=0⟹

θ1=arctan((py-d6ay)/(px-d6ax)).

类此可依次求得其他关节转角：

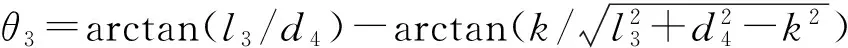
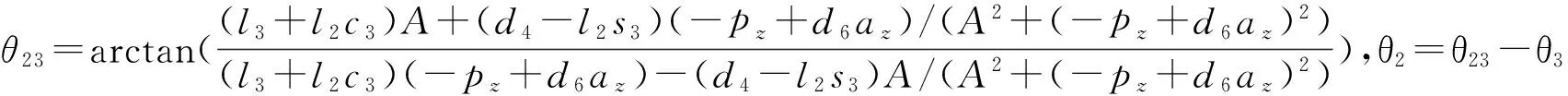
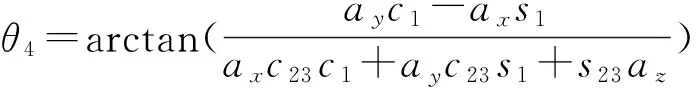
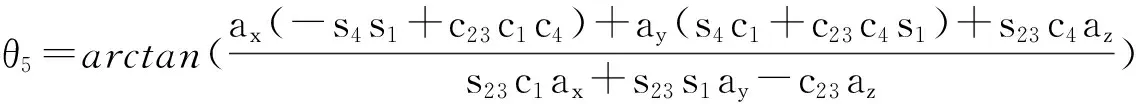
3.1 运动路径规划

为了满足机床上下料机器人的作业任务，需要对其运动路径规划进行研究，同时要考虑机器人的工作空间，它是衡量机器人作业能力范围的一个重要参数指标，通过工作空间的形状和大小来查看机器人末端的动作区域[2]。本文中机床上下料机器人的工作空间计算分析采用蒙特卡洛[3]方法，根据运动学正解在MATLAB中编写求机器人空间的程序，得到工作空间的三维点云图，如图3所示。

根据机器人所要完成的作业任务来规划末端的运动路径，机器人拟完成“中”字运动路径，其末端姿态始终与YZ平面垂直。机器人完成作业任务需要经过6个关键点，其可分成6个阶段来完成，如图4所示。

图3 机器人的工作空间 图4 “中”字的路径

规划图

3.2ADAMS运动路径仿真

将Pro/E中建立的机器人三维模型导入到ADAMS中，设置工作环境，编辑各构件的材料属性，添加各旋转运动副和驱动，导入各关节的样条驱动角度值。仿真时间设置为3s，仿真步数为200。仿真完成后，得到机器人末端的运动轨迹如图5所示。

仿真中机床上下料机器人按照设定的位姿其末端执行器完成了“中”字的轨迹运动，进一步验证了运动学正解和逆解的正确性，所求得的关节角度值可用于物理样机的驱动控制，同时可以观察机器人在整个运动过程中的运动情况，实际应用中可考察机器人避障的情况，进而也说明了机器人的机械设计能够完成机床上下料的任务。

图5 机器人各关键点的运动轨迹

4 结论

本文对机床上下料机器人进行了运动学分析，通过D-H方法得到了运动学正解和逆解，然后在工作空间范围内对上下料机器人末端的运动路径进行了规划，最后在ADAMS动力学仿真软件中进行仿真，验证了运动学求解和运动路径规划的正确性，为机床上下料机器人的轨迹规划提供了很好的理论依据。

和英文摘要参考文献：

[1] 刘极峰.机器人技术基础[M].北京：高等教育出版社,2006.

[2] 毕诸明,吴瑞珉.工业机器人的工作空间综合[J].机器人,1994(5):43-56.

[3] 崔玉洁,张祖立.基于蒙特卡洛方法的采摘工业机器人工作空间分析[J].农机化研究,2007(12):62-63.

[4] 蔡自兴.机器人学基础[M].北京：机械工业出版社，2009.

[5] Denavit J, Hartenberg R S.A kinematic notation for lower-pair mechanisms based on matrices[J].Journal of Applied Mechanics,1995,21(5):215-221.

[6] Francisco Valero, Vicente Mata, Antonio Besa.Trajectory planning in workspaces with obstacles taking into account the dynamic robot behavior[J].Mechanism and Machine Theory,2006，41:525-536.

[7] 马如奇，郝双晖，郑伟峰，等.基于MATLAB与ADAMS的机械臂联合仿真研究[J].机械设计与制造，2010(4)：93-95.

[8] 李增刚.ADAMS入门详解与实例[M].北京: 国防工业出版社, 2006.

Kinematic Analysis and Simulation of Machine Tending Robot

YU Yi-wei

(Hubei Jiuzhiyang Infrared System Co.,Ltd., Wuhan 430000, China)

This paper applies D-H coordinate method to robots’ kinematic analysis, and obtains the forward and inverse kinematic solutions. By use of Monte Carlo method, the workspace of the robot is calculated using MATLAB Programming, and then the movement path is planned in the workspace. The robot is simulated in ADAMS by using the inverse solution. The experimental data obtained for the machine tending robot provides a good theoretical basis for the robot’s design and structure optimization.

D-H coordinates; machine tending robot; simulation; kinematics

1672- 6413(2015)06- 0172- 02

2015- 07- 06；

2015- 10- 18

余伊薇(1990-)，女，湖北武汉人，助理工程师，硕士，主要从事机器自动化监测。

TP242.2

A