3-RPS和3-SPR机构的工作空间差异分析

原 政

(潞安职业技术学院 机电工程系，山西 长治 046204)

3-RPS和3-SPR机构的工作空间差异分析

原 政

(潞安职业技术学院 机电工程系，山西 长治 046204)

基于螺旋理论分别对3-RPS和3-SPR机构的自由度进行了分析，揭示了两机构由于动平台和静平台的倒置引起的运动转轴的位置变化。采用搜索法分别绘制了两机构的工作空间，揭示了转轴位置的差异引起的工作空间的不同。

3-RPS；3-SPR；螺旋理论；工作空间

0 引言

少自由度并联机构具有结构简单、制造成本低及控制容易等优点，近年来，它已成为机器人领域的研究热点之一。在各类少自由度并联机构中，两转一移三自由度(2R+1T)并联机构是比较重要的一类机构，在诸多领域得到了广泛的应用。本文采用螺旋理论对3-RPS和3-SPR机构进行深入分析，揭示由于动、静平台位置不同引起的机构运动性质和工作空间的变化。

1 3-RPS的自由度分析

如图1所示，3-RPS机构是由上、下平台皆为等边三角形的动平台abc和静平台ABC以及连接上下两个平台的3个分支构成。其中3个分支与上平台即动平台abc相连的运动副为球铰副S，与下平台即静平台ABC相连的为转动副R；在球铰副与转动副之间的为移动副P。固定坐标系O-XYZ固连在静平台上，原点O在静平台中心处，X轴沿着OA方向由O指向A，Z轴垂直于静平台向上，Y轴按右手坐标系确定。与动平台固连的坐标系Q-xyz的Q点与动平台中心固连，x轴沿Qa方向由Q指向a，z轴过Q点垂直于动平台向上，y轴按右手坐标系确定。图2为3-RPS单分支的反螺旋。

利用修正的Kutzbach-Grübler公式求解该机器人机构的自由度M，修正的Kutzbach-Grübler公式为：

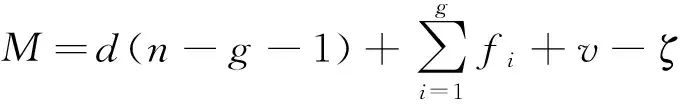
(1)

其中：d为机构的阶数；n为构件的数目；g为运动副的数目；fi为第i个运动副的自由度数；v为机构的冗余约束数；ζ为机构的局部自由度数。

3-RPS机构反螺旋的约束力为过球副中心点平行于转动副的线矢量。由于对称性，另外两个分支对静平台的约束同样为过各分支中的球铰副中心点且平行于静平台内转动副轴线的两个力线矢。这样平台就受到了3个约束力，但这3个约束力不共轴，由此可知该机构无公共约束即λ=0，无冗余约束即v=0，无局部自由度即ζ=0；在该机构中，机构的阶数d=6，构件数n=8，运动副数g=9，所有运动副具有的自由度数之和为：∑fi=15。代入公式(1)得机构的自由度数：M=3。

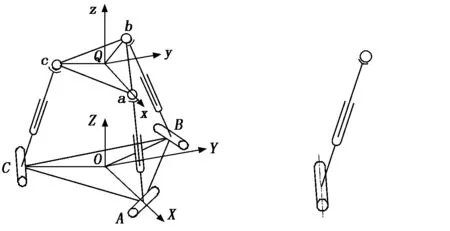
图1 3-RPS机构 图2 3-RPS单分支的反螺旋

自由度的瞬时性判断：由于求取的反螺旋的方向取决于3-RPS机构的结构特性，因此该机构任意时刻自由度性质不变。

按照螺旋理论求解RPS分支的反螺旋即约束螺旋。按照反螺旋的性质：若约束螺旋为约束力螺旋，则该螺旋必须与转动副轴线共面，且同时与移动副轴线垂直；若约束螺旋为约束力偶，则该螺旋必须与转动副轴线垂直。因此可以得到RPS分支的约束螺旋为经过球铰副中心且平行于转动副轴线方向的约束力螺旋。

由以上分析可知：动平台abc受到3个共面约束力，方向分别平行于各自分支的转动副轴线。根据图1还可以看出，动平台abc的运动螺旋为绕x轴的转动、绕y轴的转动以及沿z轴的移动即(2R+1T)。

2 3-SPR的自由度分析

针对3-SPR机构建立如图3所示坐标系。从图3中可以看出：3-SPR和3-RPS机构的主要区别在于两种机构动、静平台的运动副类型进行了互换。3-SPR机构的动平台均由转动副连接，其静平台均由球铰副连接；而3-RPS则恰恰相反，它的动平台均由球铰副连接，静平台均由转动副连接。图4为3-SPR机构单分支的反螺旋。

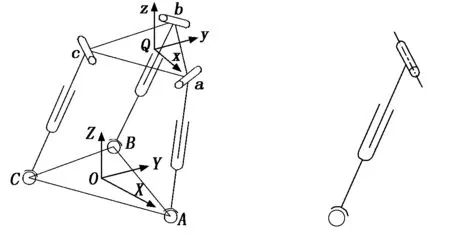
图3 3-SPR机构 图4 3-SPR单分支的反螺旋

3-SPR机构的动平台abc共受到了3个约束力，且3个约束力共面，方向分别平行于各自分支的转动副轴线，故而没有公共约束，同样没有冗余约束和局部自由度，其机构的阶数、构件数、自由度数与3-RPS机构相同。代入自由度计算公式(1)可得自由度仍然为3。

同样根据图3可以看出，动平台abc的运动螺旋也包含绕x轴的转动、绕y轴的转动以及沿z轴的移动即(2R+1T)。

3 工作空间分析

依据螺旋理论，只有与约束力共面的直线才能作为转轴。对3-RPS机构来说，约束力所在的平面即动平台所在的平面，因此转轴分布在动平台平面内；对3-SPR机构来说，约束力所在的平面为动平台运行中与静平台重合的平面，因此转轴分布在动平台与静平台重合的平面内，由此可见，两机构的转轴所在平面不同，故而导致两机构工作空间的不同。

3.1 工作空间约束条件

机构的工作空间主要受转动副转角、连杆干涉、杆长等因素的影响。结合机构的运动副和运动形式可知，机构的工作空间主要受以下几个因素的影响：①驱动副的运动范围限制；②运动副转角运动范围限制；③连杆间的干涉。据此得出机构工作空间的约束条件为：

(2)

其中：li为移动副行程；lmin、lmax分别为移动副行程的最小值和最大值；θi是球铰副的实际转角(即分支连杆方向与球铰副中心线间的夹角)；θmax为球铰副的最大允许转角；D是分支连杆的直径；Dij是两个分支间的距离。

3.2 搜索法确定工作空间

3-RPS和3-SPR机构均具有绕x轴的转动、绕y轴的转动以及沿z轴的移动这三个独立的运动。因此通过搜索动平台中心点的位置坐标可以确定机构的位置工作空间。定义欧拉角α=0和β=0时动平台中心点与静平台中心点间的距离为初始高度z。给定机构的几何约束条件以及初始高度z，可以得出机构在此初始高度条件下动平台可以达到的工作空间。

其中，移动副行程li可根据反解计算得到，设定

移动副的移动范围为：500 mm≤li≤750 mm；球铰副的转角约束条件为：

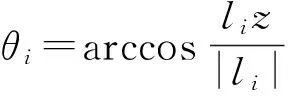
(3)

其中：i=1～3；θi≤30°；z为初始高度。

转动副的约束条件为：

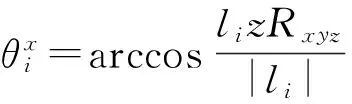
(4)

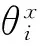
利用式(3)和式(4)进行MATLAB编程，由此得到3-RPS与3-SPR的工作空间，分别如图5和图6所示。

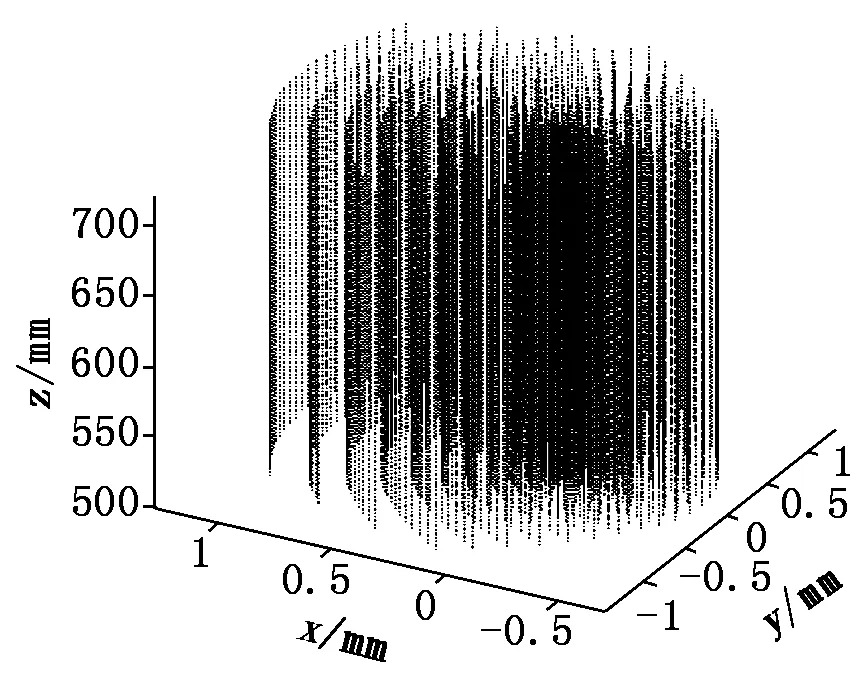
图5 3-RPS工作空间

图6 3-SPR工作空间

从图4和图5中可以看出：对于3-RPS机构，转轴分布在与动平台重合的面上，同时受到静平台约束，因此工作空间相对较小；对于3-SPR机构，转轴分布在动平台运行时与静平台重合的平面上，因此工作空间较3-RPS大很多。

4 结论

经过分析可以看出，3-RPS和3-SPR机构虽然只是动、静平台进行了互换，其自由度数和类型没有发生变化，但其工作空间的形态发生了变化，工作空间的大小也存在一定的差异。从分析结果可以看出，3-SPR机构比3-RPS机构具有更好的特性。

[1] 黄真，赵永生，赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

[2] 赵铁石,赵永生,黄真.欠秩并联机器人能连续转动转轴存在的物理条件和数学判据[J].机器人,1999(5):347-351.

[3] Huang Z,Tao W,Fang Y.Study on the kinematic characteristics of 3 DOF in-parallel actuated platform mechanisms[J].Mechanism and Machine Theory,1996,31(8):999-1007.

Analysis of Workspace Differences between 3-RPS and 3-SPR Mechanisms

YUAN Zheng

(Lu’An Vocational & Technical College, Changzhi 046204, China)

The degrees of freedom of 3-RPS and 3-SPR are analyzed separately based on screw theory, the changes of the movement shafts caused by the inversion of the moving platform and the fixed platform are pointed out. The workspaces of two mechanisms are mapped by the search method, which concludes that different movement shaft will lead to the difference of the workspace.

3-RPS; 3-SPR; screw theory; workspace

1672- 6413(2015)06- 0170- 02

2015- 09- 26；

2015- 10- 16

原政(1986-)，男，山西长治人，助教，硕士，主要研究方向为机械设计及自动化。

TP242∶TH112

A