某型号搬运机器人倍速平移机构轻量化设计

席 堃，丁晓红，汪兵兵，杨琴琴，余慧杰

(1.上海理工大学 机械工程学院，上海 200093；2.上海发那科机器人有限公司，上海 201906)

某型号搬运机器人倍速平移机构轻量化设计

席 堃1，丁晓红1，汪兵兵1，杨琴琴2，余慧杰1

(1.上海理工大学 机械工程学院，上海 200093；2.上海发那科机器人有限公司，上海 201906)

在满足一定刚度的条件下，要求搬运机器人的倍速平移机构的高速运动部件减轻质量，以减少主机器人驱动功率，达到降低成本、提高机器人的操作精度和生产节拍的目的。首先运用多刚体系统动力学分析得到倍速平移机构主梁结构所受的动态载荷；然后利用有限元法进行瞬态响应分析；最后用等效静态载荷法计算得到等效静态载荷，并将该载荷作为力边界条件，运用变密度法建立拓扑优化模型，对倍速平移机构主梁结构进行轻量化设计。与优化前模型相比，优化后主梁质量减少了8.9%，同时其刚度提高了14.0%。

搬运机器人；倍速平移机构；结构拓扑优化

0 引言

搬运机器人是一种冲压自动化系统中的搬运平台，已经被广泛地应用于汽车和航空航天行业。根据生产中的实际需求，在搬运机器人法兰盘上安装一个倍速平移机构，可实现工件在前、后压力机之间的快速平移运动。但是随之引入了两个问题：一是由于移动速度快，倍速平移机构在高速运动中会产生很大的惯性力，导致部件发生弹性变形，影响机构的定位精度；二是对于主机器人来讲，倍速平移机构也是负载，故减少了机器人的最大搬运重量。因此，为了提高搬运机器人的操作精度和生产节拍，减小主机器人的驱动功率，本文对倍速平移机构进行轻量化设计。

实现结构轻量化的重要手段之一是结构拓扑优化设计技术。Park[1]等提出等效静态载荷法，Kang[2]等将该方法应用于柔性多体动力学响应优化中，通过柔性多体动力学方程导出等效静态载荷，以之为边界条件进行静态结构拓扑优化。Hong[3]等提出运用多刚体系统动力学分析代替柔性多体动力学分析，得到动态的约束反力，通过瞬态动力学分析得到相应位移场，再借助等效静态载荷原理计算等效静态载荷，以之作为力边界条件进行系列静态结构拓扑优化。

本文运用多刚体系统动力学理论和等效静态载荷法，结合结构拓扑优化技术对某型号冲压搬运机器人的倍速平移机构的主梁结构进行轻量化设计。

1 基于等效静态载荷法的结构优化设计方法

当结构承受动态载荷时，在某一时刻，结构会发生变形，从而产生一个位移场。如果在这一时刻存在一个静态载荷作用于结构之上，该载荷产生与动态载荷作用下相同的位移场，那么称该静态载荷为这一动态载荷在这一时刻的等效静态载荷[4]。

结构的优化过程如下：

(1) 赋初值。令迭代次数p=0，xp=x0，其中x为设计变量。

(2) 根据结构运动时间将结构的运动过程等分为一定的时间步，对结构进行瞬态动力学分析。无阻尼情况下，动态载荷作用按式(1)所示的结构运动方程进行分析[5]：

(1)

其中：t为时间；M为质量矩阵；K为刚度矩阵；y为动态位移矢量；r为结构所受外部动态载荷。

(3) 进行等效静态载荷计算。将式(1)移项可得：

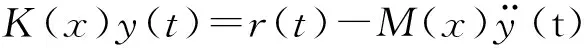
(2)

设

K(x)y(t)=feq.

(3)

其中：feq为t时刻的等效静态载荷。根据式(2)计算结构在某一时刻的等效静态载荷，可以看出，等效静态载荷包括外力和结构的惯性力，通过计算每个离散时间步可以得出它们的值。一般地，可以在每个时间步通过数值计算得出方程(1)的解，即在离散的时域中可求解式(1)，因此在离散的时域内也可以求解等效静态载荷。在i时刻，等效静态载荷可以在进行柔性多体动力学瞬态分析后求得：

(4)

其中：n为瞬态分析中所截取的时间点的个数，即等效静态载荷的数目。

(4) 使用计算所得的等效静态载荷求解线性静态响应优化问题。

(5) 比较设计变量。当p=0，令p=p+1，转到第2步；当p>0，如果‖xp-xp-1‖/‖xp-1‖<ε，优化终止，否则令p=p+1，转到第2步。其中ε是一个极小的数。

2 倍速平移机构的主梁结构轻量化设计

2.1 主梁结构的静力分析

某型号搬运机器人倍速平移机构主梁结构(如图1所示)重32.6 kg。主梁上、下各安装两对滚动导轨，主梁结构通过上导轨框架结构和机器人法兰盘连接，下导轨和端拾器连接。为了得到主梁力学性能，可以通过有限元分析法得到其位移和应力分布情况。考虑到实际工况复杂，建立有限元模型困难，故根据经验，只考虑最危险工况，即主梁一端固定，另一端施加集中力(如图1中箭头所示)的条件下，对主梁进行静力分析。主梁有限元模型如图2所示。

图1 主梁结构模型 图2 主梁有限元模型

分析得到的主梁结构位移云图和应力云图如图3和图4所示。由图3、图4可以看出，主梁结构在最危险工况下，最大位移为12.9 mm，最大应力为46.9 MPa。

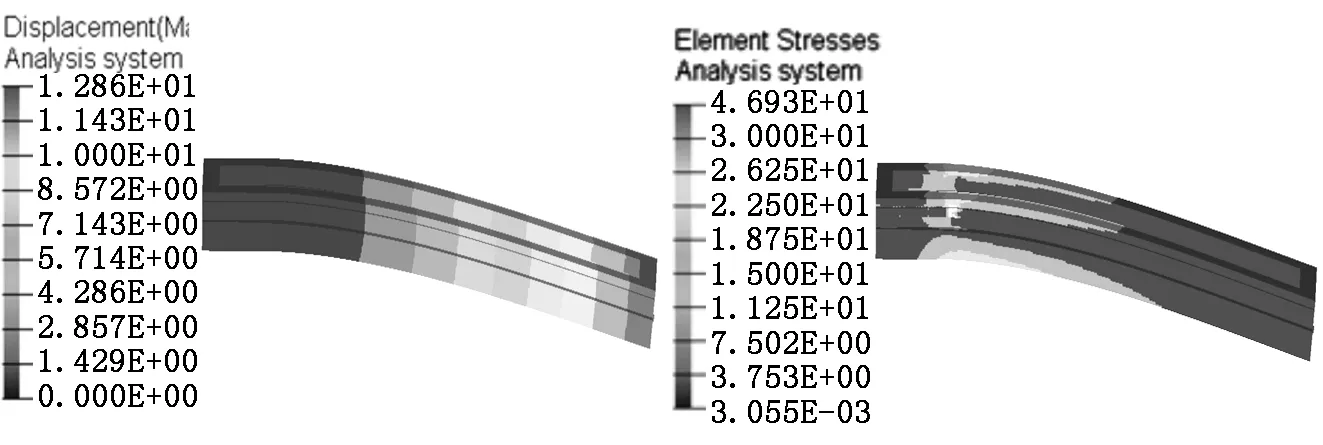
图3 主梁结构位移云图 图4 主梁结构应力云图

2.2 主梁结构拓扑优化

由于搬运机器人负载能力有限，倍速平移机构是附加的负载，其质量越大，机器人所能搬运的零件质量越小，因此要减少倍速平移机构的质量。在满足一定刚度条件下减少倍速平移机构的质量，还可以较小机器人的驱动功率，降低生产成本。结构拓扑优化技术能够在给定的空间结构中形成合理的材料分布。为了模拟主梁在现实工况中所受的载荷，本文应用多体动力学仿真分析技术建立在最危险工况下倍速平移机构的多体动力学模型，如图5所示。主梁结构作为拓扑优化对象，需要将其全部填充材料，并作为柔性体，导轨副和工件假定为刚性体。上、下两对滑动副在同步传动带的作用下做方向相反的匀速运动。设仿真时间步长为100，仿真时间为0.9 s。

采用密度法对主梁结构进行拓扑优化设计[6]。取主梁结构为设计区域，其余为非设计区域。拓扑优化数学模型为：

(5)

其中：U为主梁结构最大应变能；Vf和V0为主梁结构优化后体积及原体积；f为体积分数。

图5 最危险工况下多体动力学模型

图6为结构最大应变能的迭代历程。从图6中可以看出，在第10个迭代步，结构最大应变能趋于收敛，应变能从9 650 J减小到8 980 J。

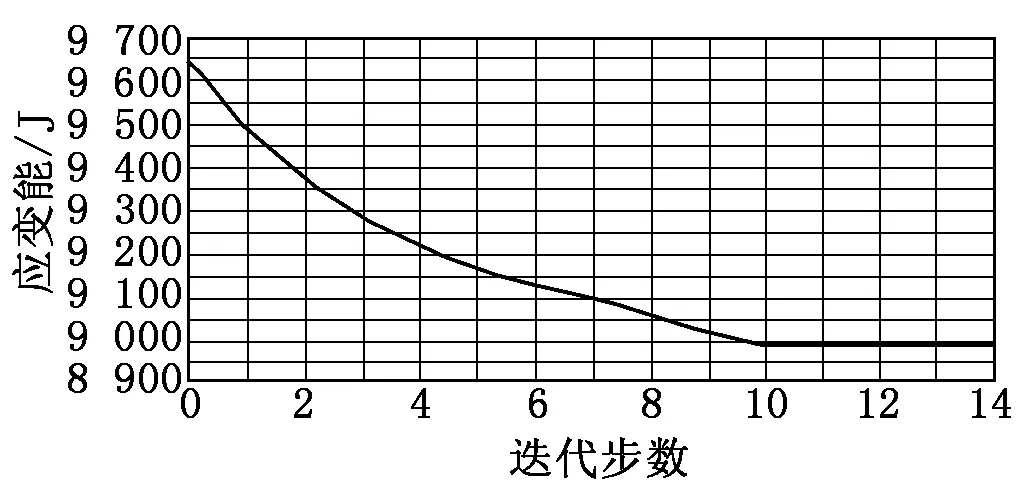
图6 主梁应变能迭代历程

图7为优化后主梁结构的单元密度云图，反映了每个单元所含材料的多少。密度为1的区域充满了材料，密度为0的区域没有材料，其他为过渡区域。根据图7中的信息，可得到拓扑优化方案。

图7 主梁结构的单元密度云图

2.3 优化后结构分析比较

根据优化结果重新设计主梁结构，如图8所示。在相同危险工况下对优化后主梁结构进行静力分析，建立有限元模型，如图9所示。

分析得到的优化后主梁的位移和应力云图如图10和图11所示。由图10和图11可以看出：优化后主梁结构在最危险工况下，最大位移为11.1 mm，比优化前结构的最大位移减小了14.0%；最大应力为40.3MPa，比优化前结构的应力减少了14.1%。优化后立梁质量由优化前的32.6 kg下降到29.7 kg，减少8.9%。

图8 优化后主梁结构示意图 图9 优化后主梁有限元模型

3 结论

本文通过运用等效静态载荷法,把动态载荷转化为等效静态载荷，然后将其作为边界条件加入优化过程，对搬运机器人倍速平移机构的主梁结构进行轻量化设计。根据主梁结构优化单元密度云图，重新设计主梁结构。整个方法使得优化后的主梁质量减少了8.9%，同时刚度提高了14.0%。研究结果表明：基于等效静态载荷法的优化方法可有效地处理高速运动机构的轻量化设计问题。

图10 优化后主梁位移图 图11 优化后主梁应力图

[1] Park G J.Analytic methods for design practice[M].London:Springer,2007.

[2] Kang B S,Park G J,Arora J S.Optimization of flexible multibody dynamics systems using the equivalent static loads[J].AIAA,2005,43(4):846-852.

[3] Hong E P,You B J,Kim C H,et al.Optimization of flexible components of multibody systems via equivalent static loads[J].Strucural and Multidisciplinary Optimization,2010,40(1-6):549-562.

[4] Choi Y H,Jang S H,Park H M,et al.A genetic algorithm based multi-step design optimization of a machine structure for minimum weight and compliance[C]//SICE Annual Conference.[s.l.]：SICE,2005:476-481.

[5] Haug E J.Intermediate dynamics[M].New Jersey: Prentice-Hall, 1992.

[6] Bendsoe M P,Sigmund O.Material interpolation schemes in topology optimization[J].Archive of Applied Mechanics,1999,69(9):635-654.

Lightweight Design of Double-speed-translational Mechanism for Transfer Robot

XI Kun1, DING Xiao-hong1, WANG Bing-bing1, YANG Qin-qin2, YU Hui-jie1

(1.School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Shanghai Fanuc Robotics Co., Ltd., Shanghai 201906, China)

Firstly, the dynamic loads on main beam of double-speed-translational mechanism are calculated by multi-rigid-body system dynamics analysis technics. Then the transient response of main beam to transient excitations is studied using the finite element method, then the equivalent static loads are calculated by the equivalent static loads method, which are used as the force boundary conditions. Finally, by variable density method, an optimal topology model is established to support the lightweight design of the main beam structure of double-speed-translational mechanism. Compared with the model without optimization, the mass of the new main beam decreases by 8.9%, while its stiffness increases by 14.0%.

transfer robot; double-speed-transtational mechanism; structural topology optimization

1672- 6413(2015)06- 0038- 03

2015- 01- 22；

2015- 08- 20

席堃(1989-)，男，甘肃兰州人，在读硕士研究生，研究方向为结构分析与优化。

TP242.3

A

上海市宝山区科学技术委员会产学研合作项目(CXY-2012-11)