一类变异型 Chebyshev－Halley迭代法的收敛性*

徐秀斌， 包振威， 何 濛

(浙江师范大学数理与信息工程学院，浙江金华 321004)

一类变异型 Chebyshev－Halley迭代法的收敛性*

徐秀斌， 包振威， 何 濛

(浙江师范大学数理与信息工程学院，浙江金华 321004)

研究了一类变异型Chebyshev－Halley迭代法的收敛性.给出了在满足条件‖F"(x)‖≤ω(‖x‖)时的迭代法收敛性判据及半局部收敛性的证明，最后分析了参数α的变化对收敛半径的影响，以期为某种参数的选择提供依据.

非线性方程;Chebyshev－Halley型迭代法;收敛判据;半局部收敛

0 引言

定义非线性算子F:Ω⊂X→Y.其中:X和Y是同型Banach空间;F具有二阶连续导数F"(x);Ω为非空开凸集.为求解方程F(x)=0，文献［1］提出了Chebyshev－Halley迭代法

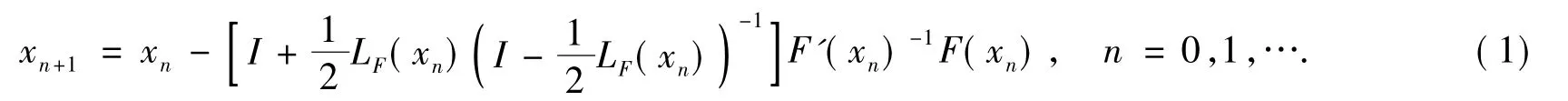
式(1)中:I为单位算子;LF(x)=F'(x)－1F"(x)F'(x)－1F(x)，x∈Ω.并且在Newton－Kantorovich条件下证明了其收敛性.随后文献［2］对更一般的Chebyshev－Halley迭代类进行了研究;文献［3－4］加入了参数α∈［0，1］，给出和分析了一类变型后的Chebyshev－Halley迭代法

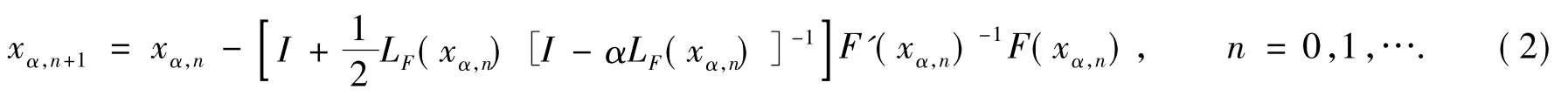
该方法包含了Chebyshev方法(α=0)、Halley方法和凸加速Newton法(即super－Halley法) (α=1).许多学者讨论了这些方法的收敛性，如文献［5］用条件‖F"(x)‖≤K和‖F‴(x)‖≤N讨论收敛性;文献［6－8］利用Lipschitz条件代替‖F‴(x)‖≤N讨论了收敛性

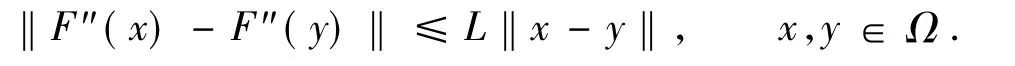
文献［3］则尝试了在Hölder条件下证明收敛性，

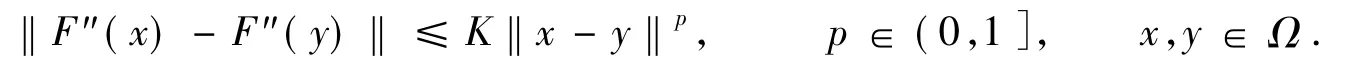
文献［1］利用如下条件讨论了收敛性:

式(3)中，ω(0)≥0，且当z＞0时，ω(z)是非减的连续实函数.

本文用‖F"(x)‖≤ω(‖x‖)，x∈Ω作为条件讨论了式(2)的收敛性，并得到了较好的结果.首先参照文献［9］，给出下列条件(记为条件(Φ)):

1)F为Banach空间X的非空开凸集Ω到Banach空间Y中的二阶可导非线性映像.

2)存在初始点xα，0∈Ω，并且Γ(xα，0)=F'(xα，0)－1存在，‖Γ(xα，0)‖≤β，‖Γ(xα，0)F(xα，0)‖≤η.

3)‖F"(x)‖≤ω(‖x‖)，x∈Ω.其中，ω(0)≥0，且当z＞0时，ω(z)是非减的连续实函数.

4)存在一个实函数φ∈C［0，1］，φ(t)≤1，使得当t∈［0，1］，z∈(0，+∞)时，ω(tz)≤φ(t)ω(z).

5)定义实函数M(t)=ω(‖xα，0‖+t)，则下列方程至少存在一个正根:

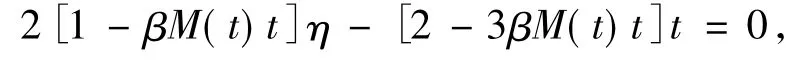
并把最小的正根记为R.

1 迭代分析和半局部收敛定理

引理1 在条件(Φ)下成立如下关系:

引理1的前3条证明可以参见文献［9］中的引理1和引理2的证明，第4条的证明不难得到，这里就不再赘述.

引理2 在条件(Φ)下，对n=0，1，…，有

定理1 在条件(Φ)下，变异型Chebyshev－Halley迭代法收敛于F(x)在B(xα，0;R)中的唯一零点x*.

2 收敛半径分析

［1］Ezquerro J A，Hernández M A.Halley's method for operators with unbounded second derivative［J］.Appl Num Math，2007，57(1):354－360.

［2］Gutiérrez J M，Hernández M A.A family of Chebyshev－Halley type methods in Banach spaces［J］.Bull Austral Math Soc，1997，55(1):113－130.

［3］Ye Xintao，Li Chong.Convergence of the family of the deformed Euler－Halley iterations under the Hölder condition of the second derivative［J］.J Comput Appl Math，2006，194(1):294－308.

［4］Ye Xintao，Li Chong，Shen Weiping.Convergence of the variants of the Chebyshev－Halley iteration family under the Hölder condition of the first derivative［J］.J Comput Appl Math，2007，203(1):279－288.

［5］Safiev R A.On some iterative processes［J］.Zh Vychisl Mat i Mat Fiz，1964，4(1):139－143.

［6］Argyros I K.The Halley method in Banach spaces and the Ptak error estimates［J］.Rev Acad Cienc Zaragoza，1997，52(2):31－41.

［7］Yamamoto T.On the method of tangent hyperbolas in Banach spaces［J］.J Comput Appl Math，1988，21(1):75－86.

［8］Candela V，Marquina A.Recurrence relations for rational cubic methods I:The Halley method［J］.Computing，1990，44(1):169－184.

［9］Hernández M A.A modification of the classical Kantorovich conditions for Newton's method［J］.J Comput Appl Math，2001，137(1):201－205.

(责任编辑 陶立方)

Convergence of the variants of a Chebyshev-Halley iteration family

XU Xiubin， BAO Zhenwei， HE Meng

(College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua Zhejiang 321004，China)

Under condition‖F"(x)‖≤ω(‖x‖)，the convergence of the variants of a Chebyshev－Halley iteration family was discussed.The convergence criterion and semi－local convergence were obtained.The impact of the change of parameter α on the convergence radius was analyzed，so a kind of choosing criterion for parameters was provided.

nonlinear equations;Chebyshev－Halley type iterations;convergence criteria;semilocal convergence

O241

A

1001－5051(2015)01－0034－07

�:2014－08－05;

2014－09－12

国家自然科学基金资助项目(61170109)

徐秀斌(1962－)，男，浙江兰溪人，教授，博士.研究方向:数值逼近.

10.16218/j.issn.1001－5051.2015.01.006