渐近非扩张型映像不动点的粘性逼近法*

李柳红， 王元恒

(浙江师范大学数理与信息工程学院，浙江金华 321004)

渐近非扩张型映像不动点的粘性逼近法*

李柳红， 王元恒

(浙江师范大学数理与信息工程学院，浙江金华 321004)

在一致凸Banach空间E的非空闭凸子集C上研究了渐近非扩张映像T不动点问题，引入了一种新的更加广泛的粘性逼近迭代算法，在适当条件下证明了该迭代序列{xn}强收敛于映像T的不动点x*∈F(T)，并且x*是一个变分不等式的解.所得结果改进和推广了其他相应结果.

粘性逼近;渐近非扩张映像;不动点;变分不等式;强收敛

0 引言

1 预备知识

2 主要结果

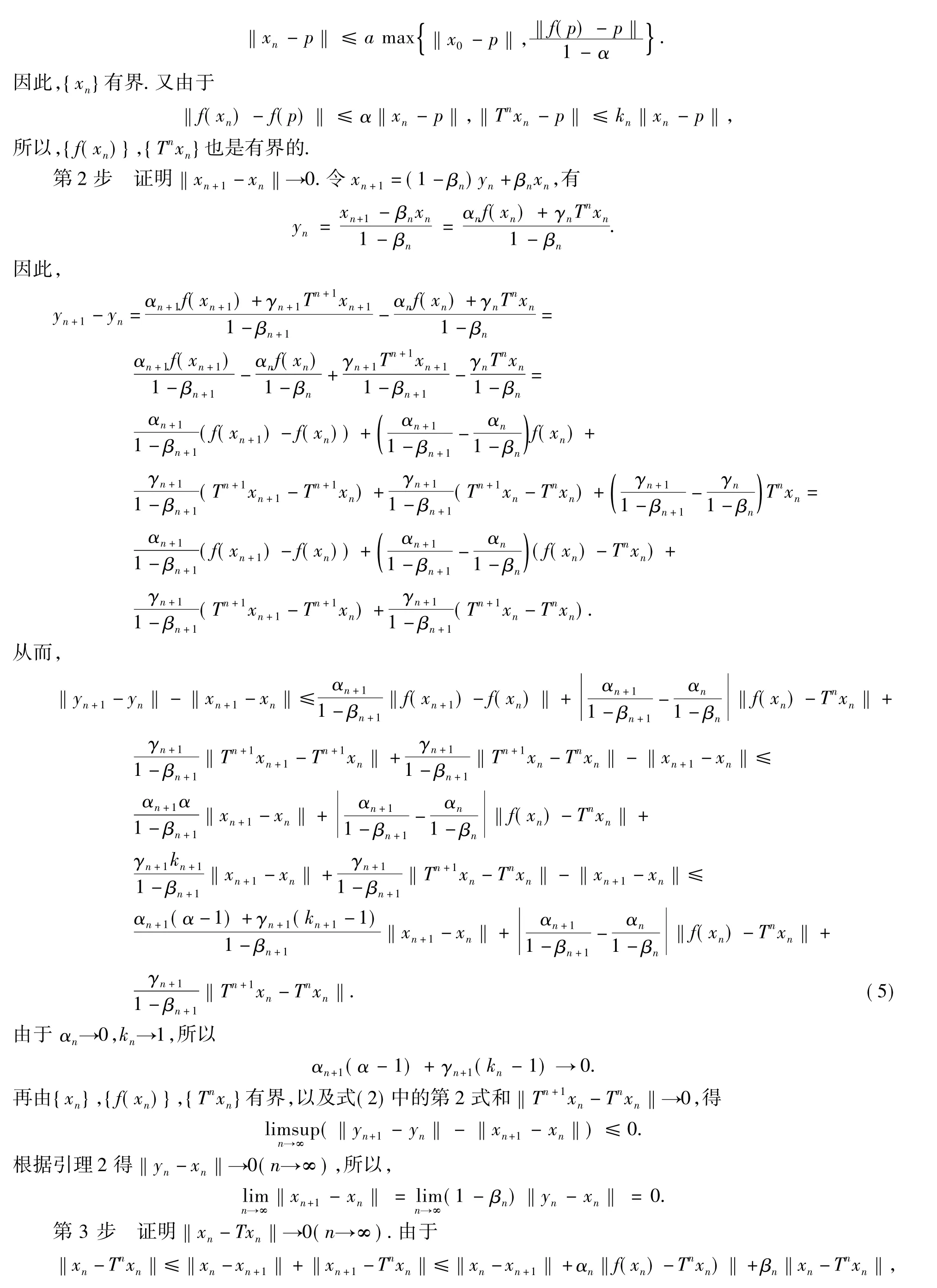
［1］Moudafi A.Viscosity approximation methods for fixed－points problems［J］.J Math Anal Appl，2000，241(1):46－55.

［2］Xu Hongkun.Viscosity approximation methods for nonexpansive mappings［J］.J Math Anal Appl，2004，298(1):279－291.

［3］王元恒，徐卫.非扩张映像不动点的一种变形迭代算法［J］.浙江大学学报:理学版，2009，36(3):259－263.

［4］Goebel K，Kirk W A.A fixed point theorem for asymptotically nonexpansive mappings［J］.Proc Am Math Soc，1972，35:171－174.

［5］曾六川.Banach空间中带误差的修正的Ishicawa迭代程序［J］.数学学报，2004，47(2):219－228.

［6］Chen Junmin，Zhang Junmin，Fan Tiegang.Viscosity approximation methods for nonexpansive mappings and monotone mappings［J］.J Math Anal Appl，2007，334(2):1450－1461.

［7］Song Yisheng，Chen Rudong，Zhou Haiyun.Viscosity approximation methods for nonexpansive mapping sequences in Banach spaces［J］.Nonlinear Anal，2007，66(5):1016－1024.

［8］赵良才，张石生.Banach空间中渐近非扩张映像具误差的强收敛性定理［J］.数学学报，2008，51(1):99－108.

［9］董家帅，王元恒，罗红平.渐近非扩张型映像的黏性三步迭代序列强收敛性［J］.浙江师范大学学报:自然科学版，2012，35(3):241－245.

［10］Ceng L C，Guu S M，Yao J C.A general composite iterative algorithm for nonexpansive mappings in Hilbert spaces［J］.Comput Math Appl，2011，61(9):2447－2455.

［11］罗红平，王元恒.三重复合修正的Ishikawa迭代序列强收敛性［J］.浙江师范大学学报:自然科学版，2013，36(1):31－36.

［12］石惠敏，王元恒.渐近伪压缩映像不动点的三步带误差修正迭代逼近［J］.系统科学与数学，2014，34(1):119－128.

［13］Wang Yuanheng，Xia Yonghui.Strong convergence of asymptotically pseudocontractions with the demiclosedness principle in Banach spaces［J］.Fixed Point Theory Appl，2012，45:1－8.

［14］Cho Y J，Zhou Haiyun，Guo Ginti.Weak and strong convergence theorems for three－step iterations with errors for asymptotically nonexpansive mappings［J］.Comput Math Appl，2004，47(4/5):707－717.

［15］Wang Yuanheng.Strong convergence theorems for asymptotically weak G－pseudo－ψ－contractive nonself－mappings with the generalized projection in Banach spaces［J］.Abstr Appl Anal，2012，2012:1－11.

(责任编辑 陶立方)

A new viscosity approximating method for the fixed points of asymptotically nonexpansive mappings

LI Liuhong， WANG Yuanheng

(College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua Zhejiang 321004，China)

A new viscosity approximating method was introduced for the fixed points of an asymptotically nonexpansive mapping T in a nonempty closed convex subset C of an uniformly convex Banach space E.Under certain appropriate conditions，it was proved that the new iterative sequence{xn}converges strongly to a fixed point x*∈ F(T)，which would be also the solution of a variational inequality.The results improved and extended the corresponding results reported by some other authors.

viscosity approximating method;asymptotically nonexpansive mapping;fixed point;variational inequality;strong convergence

O177.91

A

1001－5051(2015)01－0041－06

�:2014－06－18;

2014－09－22

国家自然科学基金资助项目(11271330);浙江省自然科学基金资助项目(LY14A010011)

李柳红(1988－)，女，江西乐平人，硕士研究生.研究方向:非线性泛函分析.

王元恒.E－mail:yhwang@zjnu.cn

10.16218/j.issn.1001－5051.2015.01.007