利用Periodic Fourier法研究橡胶混凝土隔振基础对轨道振动的影响
2015-12-05刘维宁周顺华孙晓静
金 浩,刘维宁,周顺华,孙晓静
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.北京交通大学 土木建筑工程学院,北京 100044)
利用Periodic Fourier法研究橡胶混凝土隔振基础对轨道振动的影响
金 浩1,刘维宁2,周顺华1,孙晓静2
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.北京交通大学 土木建筑工程学院,北京 100044)
地下铁道轨道减振措施研究是一个受到持续关注的问题,本文创新性地引入橡胶混凝土隔振基础这一概念。并利用Peiodic-Fourier方法,探讨了橡胶混凝土隔振基础物理参数对钢轨振动位移的影响。研究结果表明:(1)高频激励荷载引起的钢轨位移比低频激励荷载引起的钢轨位移小;(2)橡胶混凝土隔振基础刚度越大,相应的共振频率越大,但引起的钢轨振动位移越小;(3)橡胶混凝土隔振基础阻尼越大,相应的共振频率越小,且引起的钢轨振动位移也越小。
振动与波;橡胶混凝土;地下铁道;减振;Periodic-Fourier方法;钢轨位移
近几年,地下铁道引起的环境振动问题[1]和钢轨波形磨耗问题[2]日益受到关注。大量科研工作者[3-5]对环境振动预测方法和轨道减振措施进行了卓有成效的探究。经过前期的调查和分析,本文提出了一种创新性的轨道减振措施,即橡胶混凝土隔振基础[6]。
橡胶混凝土(Crumb Rubber Concrete,CRC)是一种采用废旧橡胶作为集料配制而成的新型水泥混凝土[7]。通过调配橡胶粒径大小以及橡胶的掺入量,可以调节橡胶混凝土的刚度和阻尼等物理参数。相比目前常规使用的混凝土基础,橡胶混凝土基础将具有可调节性等优点。橡胶混凝土隔振基础铺设方式如图1所示。
Periodic-Fourier方法最早见D J Mead[8]对周期结构波传播和振动响应的分析。1996年,P M Belot-serkovskiy[9]利用该方法对简谐荷载作用下的无限周期结构进行了分析。2001年,H Kruse[10]等利用前面的研究,总结出了一种用于分析线形、周期车辆-轨道结构的算法。2006年,Mohammed利用Perioic-Fourier方法,对离散浮置板轨道进行了移动简谐荷载作用和移动单点转向架的动力分析,Periodic-Fourier方法最大的特点就是运算的高效性和Fourier-repeating-uint方法相对比,同样的算例花了19分钟,而Periodic-Fourier方法仅花了2秒钟[12]。
鉴于此,本文将利用Periodic Fourier方法,分析橡胶混凝土隔振基础物理性质(刚度和阻尼)对钢轨振动的影响。

图1 橡胶混凝土隔振基础示意图
1 隔振基础数学模型
由于考虑的钢轨为离散支撑轨道,轮轨耦合作用形成的力通过扣件及支承块将以近似点荷载的形式作用在隔振基础上。因此,隔振基础对扣件的支撑作用近似为(中间支承块)串联的弹簧-阻尼系统[13]。扣件、支承块和隔振基础串联如图2所示。
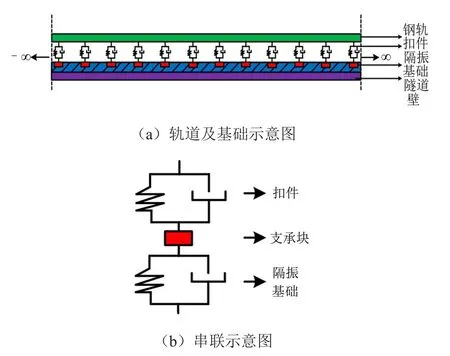
图2 扣件、支承块和隔振基础复合刚度计算示意图
扣件刚度为kfs,阻尼为cfs,则扣件复合刚度ckfs为
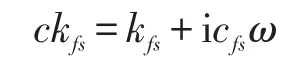
橡胶混凝土隔振基础刚度为kfo,阻尼为cfo,则橡胶混凝土隔振基础复合刚度ckfo为
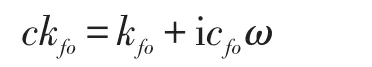
因此,扣件、支承块和橡胶混凝土隔振基础的复合刚度为
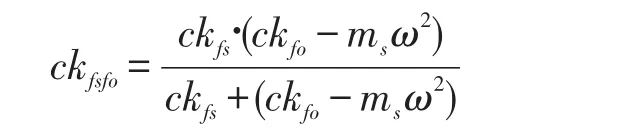
式中ms为支承块质量,角频率ω=2πf。
2 移动简谐荷载作用下轨道模型
假定钢轨为Bernoulli-Euler梁,线密度为ρ,抗弯刚度为EI。钢轨由间距为l的扣件系统支撑,扣件下面为支承块以及隔振基础。沿钢轨方向为x,x的法线方向为y。设钢轨位移为y(x,t)。单位简谐荷载eiω0t作用在钢轨上,移动速度为v,出发位置为x=0处,如图3所示。
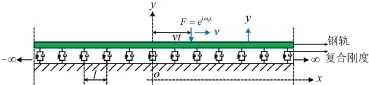
图3 移动简谐荷载作用下轨道模型
假定y(x,t)满足以下周期性条件[9]
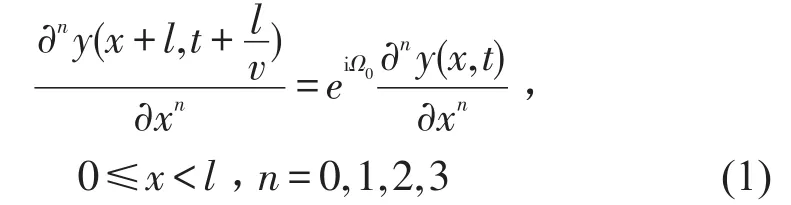
式中无量纲Ω0=ω0l/v,表示力相位随时间的变化。
根据Bernoulli-Euler梁理论,可以得到钢轨的控制方程
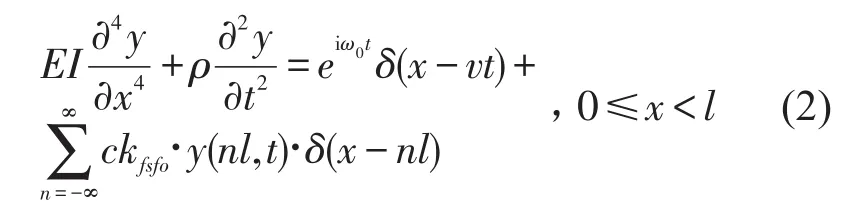
式中δ为Dirac函数。
根据周期性条件(1),可以得到相邻单元位移、变形、剪力以及弯矩之间的关系如下
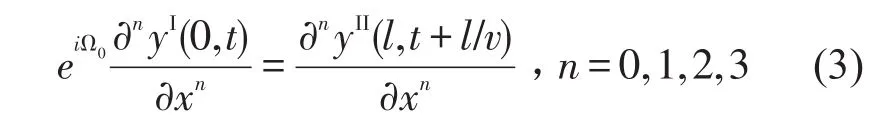
式中,上标I和II分别代表单元I和单元II。
对周期性支撑的Bernoulli-Euler梁进行受力分析,如图4单元所示。

图4 周期性单元受力分析
可以得到相邻单元位移、变形、剪力以及弯矩之间的关系
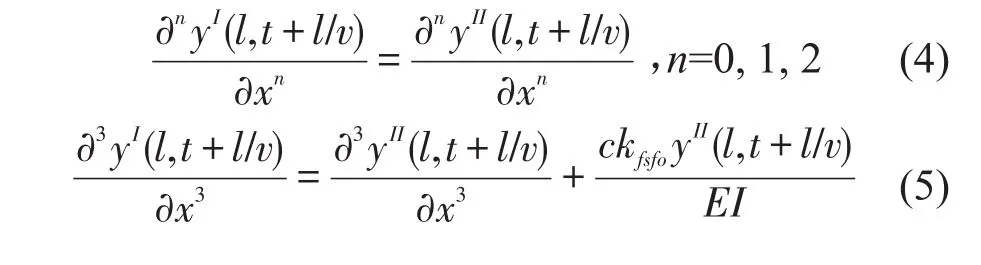
将方程(3)代入方程(4)和方程(5),可以得到公式(2)的边界条件。即对于重复性单元(譬如单元I),认为钢轨位移的零阶偏导数∂0y(x,t)/∂x0(位移)、1阶偏导数∂1y(x,t)/∂x1(变形)以及2阶偏导数∂2y(x,t)/∂x2(弯矩)在周期性支撑条件下具有式(6)关系;钢轨位移的3阶偏导数∂3y(x,t)/∂x3(剪力)在节点处不相等,具有式(7)关系。

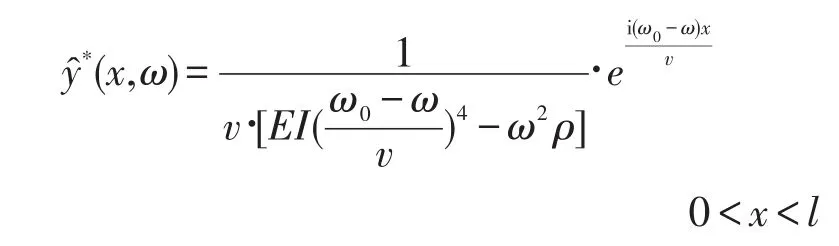
所以,方程(8)的通解为
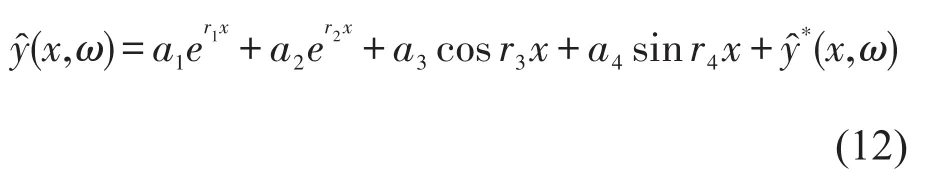
令x=0,代入方程(12),得到
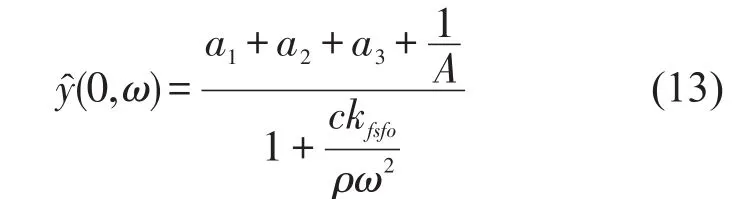
将通解(12)代入边界条件方程(9)和(10),以及结合方程(13),得到

为了方便求解以及书写清晰,将上式写成矩阵形式

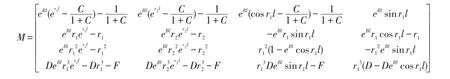
根据高斯消元法,即可得到a1,a2,a3和a4。代入式(12),得到频域下钢轨位移为
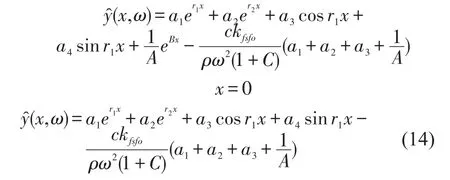
而后,通过Fourier逆变换,可以得到时域下的响应解

3 动力响应结果
钢轨线密度为ρ=60 kg/m,弹性模量E=2.1×1011Pa,截面惯性矩I=3.04×10-5m4。钢轨由间距为l=0.625 m的DTVI2扣件系统支撑,扣件刚度为kfs=7.8 ×107N/m,扣件阻尼为cfs=5×104N/(m/s)。支承块质量ms=50 kg。简谐荷载移动速度为v=10 m/s,从x=0处出发,角频率分别取ω0=640πrad/s、1 600πrad/ s和2 560π rad/s(即f0=320 Hz、800 Hz和1 280 Hz)。
3.1 不同激励荷载频率
从图5可以看出,钢轨最大位移频率由外部激励荷载频率决定;并且外部激励荷载频率越高,钢轨最大位移响应越小。
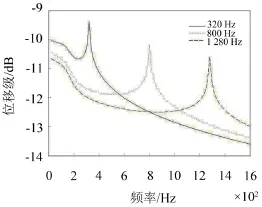
图5 钢轨位移响应(x=0.5 l,kfo=1×107N/m,cfo=1×104N/(m/s))
3.2 不同隔振基础刚度

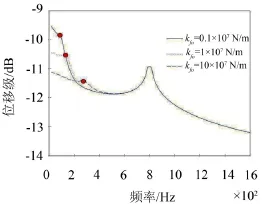
图6 钢轨位移响应(x=0.5 l,f0=800 Hz,cfo=1×104N/(m/s))
3.3 不同隔振基础阻尼
从图7可以看出,隔振基础阻尼越大,由支承块质量引起的自振频率就越小,相应幅值也越小。和隔振基础刚度对钢轨位移影响相同,外部激励频率引起的响应,不随隔振基础阻尼的改变而改变。

图7 钢轨位移响应(x=0.5 l,f0=800 Hz,kfo=1×107N/m)
4 结语
通过不同激励荷载频率、不同橡胶混凝土隔振基础刚度以及不同橡胶混凝土隔振基础阻尼对钢轨振动位移响应影响分析,得到如下结论:
(1)高频激励荷载引起的钢轨位移比低频激励荷载引起的钢轨位移小;
(2)橡胶混凝土隔振基础刚度越大,相应的共振频率越大,但是引起的钢轨振动位移越小;橡胶混凝土隔振基础阻尼越大,相应的共振频率越小,且引起的钢轨振动位移也越小。
因此,从控制钢轨振动位移的角度,宜选择高刚度和高阻尼的橡胶混凝土隔振基础。
[1]涂勤明,雷晓燕,毛顺茂.地铁产生的环境振动及轨道结构减振分析[J].噪声与振动控制,2014,34(4):178-183.
[2]刘维宁,任静,刘卫丰,等.北京地铁钢轨波磨测试分析[J].都市快轨交通,2011,24(3):6-9.
[3]金浩,刘维宁.蚁群算法耦合LS-DYNA梯式轨枕轨道动力特性优化[J].振动与冲击,2013,32(2):24-28.
[4]王文斌,刘维宁,孙宁,等.基于脉冲激励的地铁运营引起邻近建筑物内振动预测方法[J].中国铁道科学,2012,33(4):139-144.
[5]黄凯,白鸿柏,路纯红,等.应用复合减振器的梯形轨枕提高轨道的减振效果[J].噪声与振动控制,2013,33(5):161-165.
[6]金浩.基于改进蚁群算法梯式轨道及橡胶混凝土隔振基础优化研究[D].北京:北京交通大学,2013.
[7]刘春生.橡胶集料混凝土的耐久性能及在桥面铺装上的应用研究[D].天津:天津大学,2010.
[8]Mead D J.Vibration response and wave propagation in periodic structures[J].Journal of Engineering for Industry,1971,93:783.
[9]Belotserkovskiy P M.On the oscillations of infinite periodic beams subjected to a moving concentrated force[J]. Journal of Sound and Vibration,1996,193(3):705-712.
[10]Kruse H,Popp K.A modular algorithm for linear,periodic train-track models[J].Archive of Applied Mechanics, 2001,71(6):473-486.
[11]Hussein M,Hunt H.Modelling of floating-slab track with discontinuous slab Part 2:response to moving trains[J]. Low Frequency Noise,Vibration and Active Control, 2006,25(2):111-118.
[12]Hussein M,Hunt H.Modelling of Floating-Slab Track with Discontinuous Slab Part 1:Response to Oscillating Moving Loads[J].Low Frequency Noise,Vibration and Active Control,2006,25(1):23-39.
[13]贾颖绚.基于解析的车轨耦合模型及地铁对环境的振动影响研究[D].北京:北京交通大学,2009.
Study on Vibration Reduction Characteristics of the CRC Foundation Using Periodic-Fourier Method
JIN Hao1,LIU Wei-ning2,ZHOU Shun-hua1,SUN Xiao-jing2
(1.Key Laboratory of Rood and Traftic Engineering of Ministry of Education,Tongi University, Shanghai 201804,China; 2.School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China)
A novel type of a crumb rubber concrete(CRC)foundation was proposed for vibration reduction of railway tracks of subways.The Periodic-Fourier method was adopted to build the mathematical model and analyze the influence of different physical parameters of the CRC foundation on the vibration displacement of the rails.The results show that in comparison with the conventional foundations,the rail displacement induced by high-frequency excitation is greatly reduced, and the rail displacement induced by high-frequency excitation is smaller than that by low-frequency excitation;the larger stiffness of the CRC foundation can lead to larger resonant frequency and smaller vibration displacement of the rails;increasing the damping of the CRC foundation can reduce the resonant frequency and the vibration displacement of the rails.
vibration and wave;crumb rubber concrete(CRC);subway;vibration reduction;periodic-Fourier method;rail displacement
U231
A
10.3969/j.issn.1006-1335.2015.02.031
1006-1355(2015)02-0144-05
2014-12-03
国家自然科学基金项目(51278043);国家自然科学基金项目(51408033);高等学校博士学科点专项科研基金(20110009120023)
金浩(1986-),男,浙江诸暨人,讲师,博士,从事轨道振动控制研究。E-mail:zhujijinhao@gmail.com
