风电机组齿轮箱传动系统建模与动力学特性仿真分析

董 健，胡 亮，程志学，柳亦兵

（华北电力大学 能源动力与机械工程学院，北京 102206）

风电机组齿轮箱传动系统建模与动力学特性仿真分析

董 健，胡 亮，程志学，柳亦兵

（华北电力大学 能源动力与机械工程学院，北京 102206）

针对目前风电机组常见的两级行星轮系加一级平行轴传动的齿轮箱结构，建立其传动系统虚拟样机模型。基于Hertz弹性接触理论建立仿真齿轮啮合刚度计算公式；借助ADAMS动力学分析软件，对轮齿动态啮合力进行仿真，研究轮齿啮合力在齿轮转动过程中的变化规律；将输出级小齿轮柔性化，建立传动系统的刚柔耦合模型，分析仿真过程中输出级小齿轮的应力变化。利用ADAMS对复杂齿轮箱传动系统进行动力学建模与仿真取得很好的效果，为传动系统的动态设计及优化提供依据。

振动与波；齿轮箱；虚拟样机；动力学分析；动态响应

风电机组齿轮箱作为风电机组中的重要组成部分，其主要功能是传递扭矩和升速。行星齿轮传动由于其结构紧凑、传动比大、传动平稳等优点，被广泛用于机械传动的各个领域。风电机组齿轮箱传动系统多采用行星齿轮加平行轴齿轮复合传动的形式。国内外学者对齿轮箱做了大量研究。李润方、王建军等在文献[1]中系统的阐述了齿轮系统动力学的基本理论及分析方法。陈裴等[2]基于ADAMS多体动力学仿真软件，对行星齿轮进行刚柔耦合仿真，分析了太阳轮发生故障后的动力学响应。朱才朝等[3]在考虑齿轮系统时变刚度、齿侧间隙和制造误差的基础上，建立了具有多级齿轮传动的大型风电齿轮箱的齿轮—传动轴—箱体系统耦合非线性动力学模型，在考虑系统内部激励的情况下对整个耦合系统动态特性进行了研究。Gang Liu，Robert G. Parker等[4]考虑齿轮副摩擦力及其弯曲效应，对单齿轮副的动态特性进行了分析。Woohyung Kim等在文献[5]中分析了由轴承变形引起的齿轮时变压力角及重合度对行星齿轮动态响应的影响。刘振皓、巫世晶等[6]以ADAMS软件为平台建立了复合行星齿轮传动系统的虚拟样机模型，对其动力学特性进行仿真研究，为改善系统动力学特性及实现系统的动态设计提供依据。李兴然等[7]利用Pro/E软件建立了配气机构的三维实体模型，结合ANSYS软件和ADAMS软件，建立了配气机构的多柔体动力学模型。但是目前对于两级行星齿轮传动系统动力学特性的研究文献较少。

本文利用Pro/E和ADAMS软件建立了两级行星齿轮传动加一级平行轴齿轮传动系统的虚拟样机模型，并对其动力学特性进行了仿真分析。

1 基于ADAMS的动力学理论

ADAMS中定义刚体的广义坐标时采用质心的笛卡尔坐标和反应刚体方位的欧拉角，即考虑约束方程，ADAMS利用带拉格朗日乘子的拉格朗日第一类方程的能量形式得到如下方程

T为系统广义坐标表达的动能，qj为广义坐标，Qj为广义坐标qj方向的广义力，最后一项为约束方程和拉格朗日乘子在广义坐标qj方向的约束反力。

引入广义动量Pj

由系统运动方程、约束方程构成的系统动力学微分代数方程为

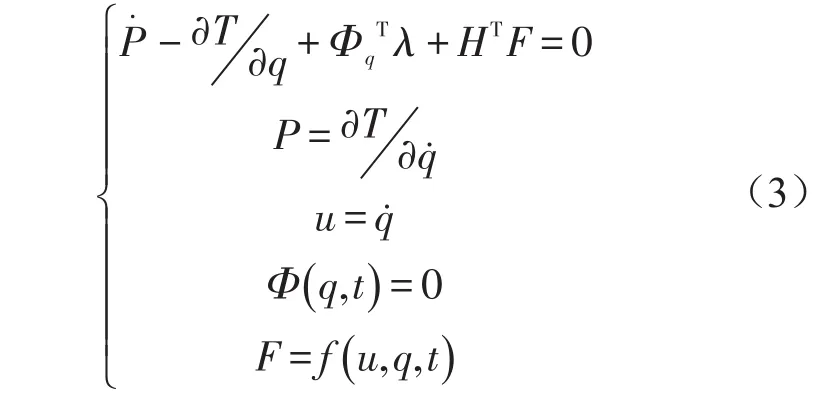
其中Φ为约束函数，Φq为约束方程的Jacobian矩阵，λ为拉格朗日乘子，H为外力坐标转换矩阵，F为系统所受外力。

为避免微分方程的Jacobian矩阵出现病态，可采用降阶积分方法。利用SI 2降阶积分方法对微分代数方程进行变换，得到公式

ADAMS中采用变系数的BDF刚性积分法对式（4）所示的动力学微分方程进行求解[8]，BDF刚性积分方法是一种自动变阶、变步长的预估校正法，主要分为预估阶段、校正阶段和误差控制阶段。

在预估阶段，根据当前时刻的系统状态矢量值，用泰勒级数预估下一时刻系统的状态矢量值

式中时间步长h=tn+1-tn。这种预估算法得到的新时刻的系统状态矢量值通常不准确，可以由Gear k+ 1阶积分求解程序来校正。

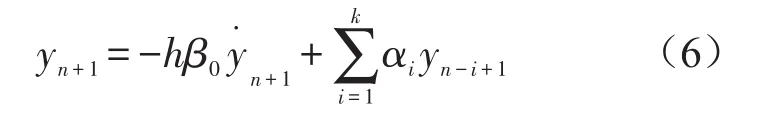
式中 yn+1为 y(t)在t=tn+1时的近似值；β0和 αi为Gear积分程序的系数值。式（6）经过整理，可以表示为

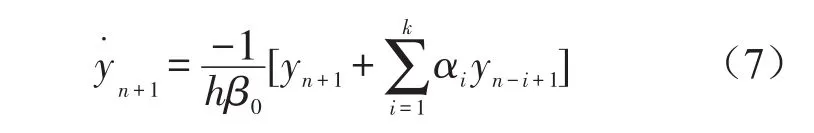
在校正阶段，将状态变量的值代入系统方程G(y,y·,t)=0，如果方程成立则状态变量就为方程的解；若G(y,y·,t)≠0，利用修正的Newton-Raphson求解线性方程得到Δy，更新y，使系统方程更接近于成立。JΔy=G(y,y·,tn+1)，其中J为系统的雅克比矩阵。重复上述步骤，直到Δy足够小。

在误差控制阶段，对状态向量的预测值与校正值进行比较，如果误差过大，则舍弃此解；如果误差在允许范围以内，则接受此解。不论误差大小，都要对步长h和阶数n进行求解，直到达到仿真结束时间停止。

2 传动系统虚拟样机模型

2.1 模型建立

本文所研究风电机组齿轮箱传动系统为两级行星齿轮加一级平行轴齿轮传动形式，其结构简图如图1所示，啮合副1、3为内啮合，啮合副2、4、5为外啮合。

传动系统关键齿轮部件参数如表1所示，按表格参数利用三维绘图软件Pro/E建立传动系统各部件三维模型并进行装配，经检验确保系统无干涉后，另存为x_t文件格式导入到ADAMS中，定义材料属性，得到传动系统虚拟样机模型如图2所示。

2.2 添加约束

ADAMS约束库中提供了多种约束类型，常用的约束有旋转副（joint）、固定副（fixed）以及接触（contact）。根据实际的运行情况在零件之间以及零件与大地（ground）之间添加约束：主轴与大地、太阳轮与大地、行星轮与行星架、输出级齿轮与大地之间添加转动副；行星轮与太阳轮、行星轮与齿圈、输出级齿轮之间添加接触；主轴和低速级行星架、低速级太阳轮和中间级行星架、齿圈和大地之间添加固定副。传动系统虚拟样机模型中共包含10个旋转副、6个固定副、13个接触副。

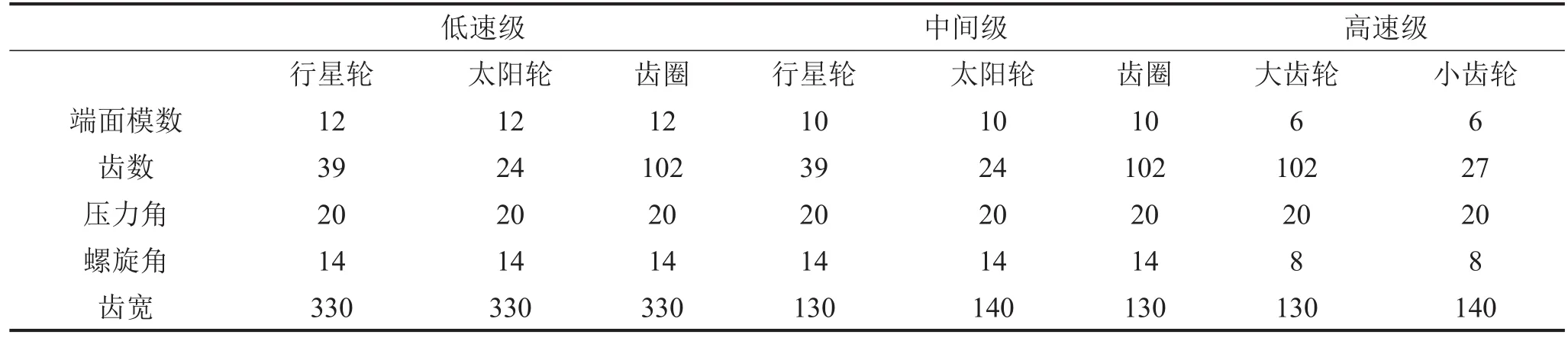
表1 传动系统关键齿轮部件参数

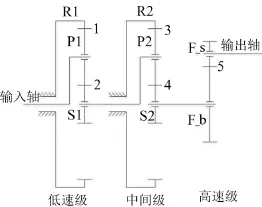
图1 传动系统结构简图

图2 传动系统虚拟样机模型

2.3 定义接触

两个构件的表面发生接触时，构件就会在接触的位置产生接触力。ADAMS中可以通过定义接触模拟轮齿的啮合过程。ADAMS中计算接触力的方法有冲击函数法和补偿法[9]。冲击函数法根据Hertz弹性接触理论，采用Impact函数提供的非线性等效弹簧阻尼模型作为接触力的计算模型，接触力由两部分组成：一是由于两构件相互渗入而产生的弹性力；另一个是由于相对速度产生的阻尼力。本文采用冲击函数法计算轮齿接触力。基于冲击函数法的轮齿接触力的计算公式为：

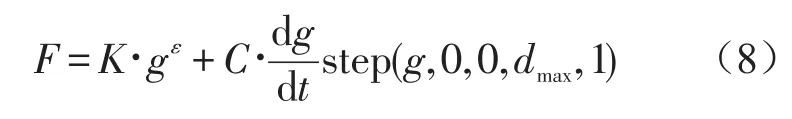
式中K为刚度系数；g为碰撞过程中相互渗入的深度；e为碰撞指数；C为阻尼系数；step为阶跃函数；dmax为碰撞过程最大允许穿透深度。

刚度系数K取决于相互碰撞物体的材料和结构形式，计算公式为

式中R为综合曲率半径，E为综合弹性模量，可由下式计算

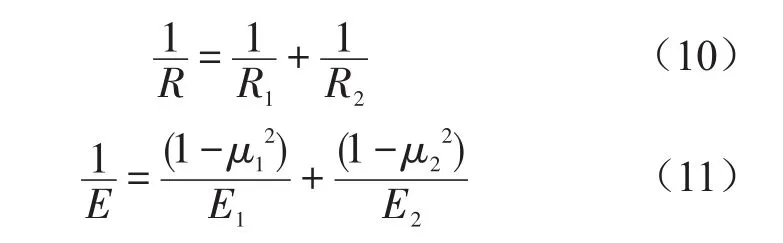
将式（10）、式（11）代入到公式（9）得到

式中E1、E2为两个接触齿轮材料的弹性模量；μ1、μ2为两个接触齿轮材料的泊松比；R1、R2为两接触齿轮接触点的当量半径，由于齿轮的齿高和分度圆半径相比较小，因此变动范围不大，可近似以分度圆上的值来代替，这样的近似误差不大[10]。

齿轮的弹性模量E1=E2=2.1×105MPa，泊松比μ1=μ2=0.29。根据经验，最大穿透深度dmax取0.2 mm，阻尼系数C取30N/(s·mm)，碰撞指数e取1.5。

2.4 斜齿轮受力分析

斜齿轮啮合过程中，轮齿所受总法向力Fn处于与轮齿相垂直的法面上，可分解为轴向力Fa、径向力Fr、圆周力Ft，计算公式为

式中αn为齿轮法向压力角，β为齿轮螺旋角，T为齿轮所受转矩，P为功率单位是kW，n为转速，单位是r/min。

对行星齿轮与太阳轮啮合副，其受力如图3所示。

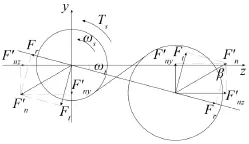
图3 行星齿轮与太阳轮啮合副受力分析

图中Ts为太阳轮所受转矩，ωs为太阳轮角速度，ω为行星架角速度，斜齿轮所受总法向力Fn在斜齿轮旋转平面内的投影太阳轮所受轮齿接触力沿y，z方向的接触力为

3 动力学仿真

3.1 设置仿真条件

齿轮箱输入转速为17.4 r/min，总传动比为104.125，结合各级齿轮齿数算出第一级行星齿轮啮合频率为29.58Hz，第二级行星齿轮啮合频率155.295 Hz，输出级齿轮啮合频率为815.298 8 Hz。

为使输入转速不出现突变，在主轴上以STEP函数添加一个速度驱动在0.2 s时转速达到104.4º/s即17.4 r/min，并保持不变。在输出级齿轮添加一个负载转矩大小为7.9×106N·mm，设置仿真时间为1 s，仿真步长为0.000 1 s。

3.2 运动学分析

图4为齿轮箱传动系统稳定运行时各级齿轮角速度曲线，从仿真结果可以看出，稳定运行时各级齿轮角速度在均值附近波动，包含有明显的周期成分。

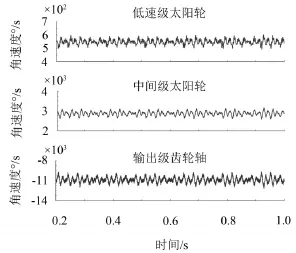
图4 齿轮箱传动系统各级齿轮角速度曲线

各级齿轮角速度仿真结果与理论计算结果如表2所示，仿真结果与理论计算结果十分接近，误差很小。

表2 各级齿轮角速度仿真值与理论值对比（º/s）

3.3 动力学分析

图5为低速级行星齿轮与太阳轮啮合齿轮副作用在太阳轮上啮合力矩的时域波形及其频谱。从图中可以看出传动系统稳定运行时，作用在太阳轮上的啮合力矩在均值附近波动，并含有一定的周期成分，啮合力矩的均值为5.21×107N·mm，表明渐开线齿轮在啮合过程中存在冲击振动。从频谱中可以看出，啮合力矩时域波形中主要频率成分为第一级啮合频率的2倍频，同时包含了第一级啮合频率1倍频、3倍频等成分。

图5 低速级行星齿轮与太阳轮啮合力矩时域波形及其频谱

图6为中间级行星齿轮与太阳轮啮合齿轮副作用在太阳轮上的啮合力矩的时域波形及其频谱。从图中可以看出，传动系统稳定运行时中间级太阳轮所受啮合力矩同低速级太阳轮所受啮合力矩具有同样的规律：在均值上下波动，同时包含一定的频率成分，啮合力矩的均值为9.95×106N·mm。从其频谱图中可以看出，太阳轮所受啮合力矩中包含有多种频率成分，图中谱线59.23 Hz对应第一级啮合频率的2倍频，310.29 Hz对应第二级啮合频率的2倍频。

输出级啮合齿轮副作用在输出轴上的啮合力矩的时域波形及其频谱如图7所示，从图中可以看出作用在输出轴上的啮合力矩具有明显的周期成分，啮合力矩在一个均值上下波动，啮合力矩的均值为8.024×106N·mm。从其频谱中可以看出输出轴所受啮合力矩中明显的频率成分为30.54 Hz，对应输出轴的转频，同时还包含了输出级啮合频率的1倍频以及2倍频等成分。

图6 中间级行星齿轮与太阳轮啮合力矩时域波形及其频谱

图7 输出级齿轮副啮合力矩时域波形及其频谱

表3为各级齿轮所受力矩的理论值与仿真值对比。从表中可以看出仿真得到各级齿轮所受啮合力矩的均值与理论计算值十分接近。

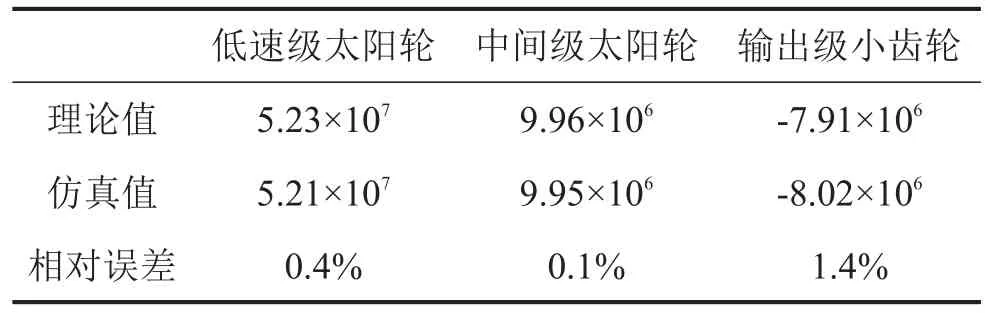
表3 各级齿轮所受力矩仿真值与理论值对比（N·mm）

图8为中间级太阳轮所受轮齿接触力在y方向和z方向的分量。从图中可看出中间级太阳轮所受y方向接触力和z方向接触力变化规律相似，相位差大约为90°，与理论分析结果一致。

图8 中间级太阳轮所受接触力在y、z方向分量

轮齿啮合力中径向力和圆周力分量对轴承的选型以及轴的优化设计十分重要。图9给出了输出级齿轮副啮合力圆周力分量的时域波形及其频谱，圆周力分量的均值为-9.61×104N，从其频谱图中可以看出圆周力分量中主要的频率成分为输出级啮合频率的1倍频成分，同时还包含低速级啮合频率的2倍频、中间级啮合频率的2倍频以及输出级啮合频率的2倍频成分等。

图9 输出级齿轮副啮合力圆周力分量时域波形及其频谱

输出级齿轮副啮合力径向力分量的时域波形及其频谱如图10所示，径向力分量均值为3.69×104N。对比径向力分量频谱图和圆周力方向频谱图可以发现，信号中包含有相同的频率成分，轴承选型及输出轴的设计时应使轴承和轴的固有频率避开圆周力和径向力中包含的频率成分。

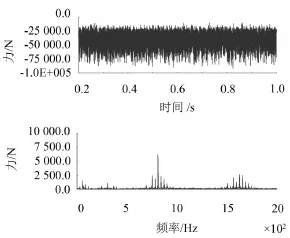
图10 输出级齿轮副啮合力径向力分量时域波形及其频谱

3.4 刚柔耦合分析

风电机组齿轮箱实际运行时，输出级小齿轮发生故障的概率较高，因此将输出级小齿轮柔性化后导入到ADAMS中建立传动系统的刚柔耦合模型。模型仿真条件同刚体模型一致，仿真得到小齿轮最大应力为55.96 MPa。图11为应力最大处节点的应力时间历程曲线，从图中可以看出应力变化具有一定的周期性。

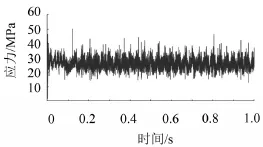
图11 应力最大处节点应力时间历程曲线

4 结语

本文以风电机组齿轮箱中常见的两级行星齿轮加一级平行轴齿轮传动结构为研究对象，利用ADAMS动力学仿真软件建立了其传动系统的虚拟样机模型，对传动系统的动力学特性进行仿真分析，得出如下结论：

(1)仿真得到各级齿轮的角速度以及啮合力幅值与理论计算值十分接近，误差很小；

(2)稳定运行时啮合力中包含明显的动载成分，从啮合力频谱中可以发现信号中包含了丰富的频率成分，其中各级啮合频率的1倍频、2倍频等高频成分突出，对传动系统的的振动信号进行分析时应重点关注这些频率成分；

(3)输出级小齿轮危险点处的应力变化具有明显的周期性，其最大应力小于小齿轮材料的屈服应力。

对常见的风电机组齿轮箱传动系统虚拟样机的动力学特性进行仿真研究，为改善传动系统动力学特性，实现传动系统的动态设计提供了一定的指导依据。

致谢

本文的工作得到中国华能集团公司科技项目“风机设备状态监测及故障诊断系统的研制”（HNKJ13-H20-05）资助，在此表示衷心的感谢。

[1]李润方，王建军.齿轮系统动力学[M].北京：科学出版社，1997.

[2]陈裴，荆建平.行星齿轮断齿故障动力学仿真与故障提取[J].噪声与振动控制，2014，34(05)：182-186.

[3]朱才朝，黄泽好，唐倩，等.风力发电齿轮箱系统耦合非线性动态特性的研究[J].机械工程学报，2005，41(8)：203-207.

[4]Gang Liu,Robert G Parker.Impact of tooth friction and its bending effect on gear dynamics[J].Journal of Sound and Vibration,2009,320(4-5):1039-1063.

[5]Woohyung Kim,Ji Yeong Lee,Jintai Chung.Dynamic analysis for a planetary gear with time-varying pressure angles and contact ratios[J].Journal of Sound and Vibration,2012,331(4):883-901.

[6]刘振皓，巫世晶，潜波，等.复合行星齿轮传动系统虚拟样机仿真研究[J].中国机械工程，2012，23(16)：1962-1966.

[7]李兴然，张保成，续彦芳，等.配气机构多柔体系统动力学仿真[J].噪声与振动控制，2010，30(3)：74-77.

[8]陈立平.机械系统动力学分析及ADAMS应用教程[M].北京：清华大学出版社，2005.

[9]李增刚.ADAMS入门详解与实例[M].北京：国防工业出版社，2012.

[10]龙凯，程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真，2002，19(6)：16-22.

Modeling and Dynamic SimulationAnalysis of Wind Turbine Gearbox Transmission System

DONG Jian,HU Liang,CHENG Zhi-xue,LIU Yi-bing
（School of Energy,Power and Mechanical Engineering,North China Electric Power University, Beijing 102206,China)

Virtual prototype model of the drive system of a wind turbine generator with a common gearbox of twostage planetary and one-stage parallel shaft gear transmission was built.Based on the Hertz elastic contact theory,the formula of gear mesh stiffness was established.By means of the dynamics analysis software ADAMS,the dynamic performance of the gear meshing was simulated and the meshing force was obtained.Then,the rigid-flexible model of the transmission system with a flexible output-stage pinion was established,and the stress variation of the pinion was analyzed. It is shown that the method of using ADAMS for dynamic simulation and modeling of complicated gear transmission system is very effective.The simulation results can provide some useful reference for gearbox optimal design.

vibration and wave;gearbox;virtual prototype;dynamic analysis;dynamic response

TH113；TH132.4

A

10.3969/j.issn.1006-1335.2015.03.020

1006-1355(2015)03-0092-06

2014－12－12

董健（1982－），男，博士生，主要研究方向：机械系统动力学特性分析。E-mail:dongjian@gdupc.cn