考虑声振耦合的平板结构声振特性优化研究
2015-12-05周奇郑王德石李永哲
周奇郑,王德石,李永哲
(海军工程大学,武汉 430033)
考虑声振耦合的平板结构声振特性优化研究
周奇郑,王德石,李永哲
(海军工程大学,武汉 430033)
研究多个动力吸振器优化结构的声振特性。根据Hamilton变分原理建立多个动力吸振器—平板—介质系统的声振耦合动力学方程,给出简支边界条件下耦合方程的解;以吸振器的质量、刚度、阻尼和位置为设计变量,以平板结构表面平均振速级和辐射声功率级为优化目标,采用遗传算法进行优化研究。研究表明:在一定频段内,单个动力吸振器能够降低优化目标10 dB左右,采用多个动力吸振器能够控制结构较宽频带的噪声;对于水下结构,可采用两个动力吸振器进行优化,但不能将空气中吸振器的优化结果直接用于水下结构。研究结果可为动力吸振器的减振降噪设计提供理论依据。
振动与波;声振耦合;平板;动力吸振器;遗传算法;声振优化
结构声振优化设计是采用附加质量、动力吸振器等方式改变结构表面速度分布,使结构成为弱辐射体。在多个动力吸振器-结构-介质系统中,吸振器与结构的振动耦合以及结构振动与其表面声压的耦合,使得系统的声振研究变得更为复杂。由于水介质的特性阻抗是空气的三千多倍,对于水下结构的声振优化问题必须考虑流体介质对结构的反作用。因此,本文将研究含声振耦合效应平板结构声振特性的优化问题。
1975年,Lang和Dym首次提出了结构声辐射的优化问题,以厚度和密度为设计变量,优化了双层板间的传声损失[1]。之后,Naghshineh等通过优化结构表面的速度分布使结构辐射声功率最小,即使结构成为弱辐射体[2]。Koopmann等用有限元计算结构的表面振速,用波叠加法计算结构的辐射声功率,以附加质量块的位置为设计变量,优化了振动结构表面的声功率[3]。文[4]在此基础上,用一组结构模态振型叠加重构结构表面形状,以每阶模态振型权系数为设计变量,采用遗传算法优化配置每阶模态振型权系数获得最优结构形状,以达到声辐射功率最小的目的。动力吸振器结构简单,能够有效抑制频率范围较小的结构的振动,在工程实践中得到了广泛应用[5]。文[6]在对飞机壁板附加动力吸振器后振动分析的基础上,设计了适合飞机壁板安装的动力吸振器并进行了实验研究,结果与理论分析一致。文[7]以电磁吸振器的质量、刚度、阻尼和位置为设计变量,优化了平板的辐射声功率,并进行了实验研究。文[8]忽略结构修改后固有频率的变化,将设计变量看作外部阻抗,对结构的表面振速进行了重新分布,给出了一种基于模型修改使结构辐射声功率最小的方法。这些研究都是先求出结构表面振速,然后根据边界元或波叠加法给出结构的辐射声功率,目前将流体介质的反作用考虑在结构声振优化中的研究很少。
基于此本文将流体介质的声压耦合在平板结构的动力学方程中,用模态展开法给出动力吸振器-平板-介质耦合系统的近似解析解,然后以吸振器的质量、刚度、阻尼和位置为设计变量,研究耦合系统的声振优化问题。
1 平板—吸振器声振耦合动力学方程
研究置于无限大声障板中平板结构的声振优化问题如图1所示,平板上布置有Q个动力吸振器。平板的结构参数:弹性模量为E,密度为ρ,泊松比为μ;几何参数:长为a,宽为b,厚度为h,作用在平板上的激励力为F(t)=F0ejωt,作用在平板表面的声压为p(x,y,0,t)。平板上(xi,yi)处布置的第i个动力吸振器的质量为mi,刚度为ki,阻尼为ci。假设平板中面上各点仅作沿z轴方向的微幅振动,位移为w,动力学吸振器的振动位移为ui,下面根据Hamilton变分原理导出多个动力吸振器-平板-介质系统的声振耦合方程。
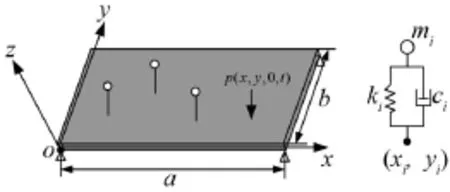
图1 含动力吸振器平板的声振模型
根据Kirchhoff假设,平板的势能可表示为

这里假定作用在平板上的力为点激励力,激励位置为(x0,y0)。
Q个动力吸振器的动能为

其势能为

吸振器阻尼力所做虚功为

根据Hamilton变分原理,得吸振器-平板的声振耦合动力学方程为

根据Green公式,有

其中δ()为Dirac函数。
2 声振耦合方程求解
根据模态展开法,平板在强迫激励下的振动位移可表示为

其中ψmn(x,y )为振型函数,对于四边简支平板
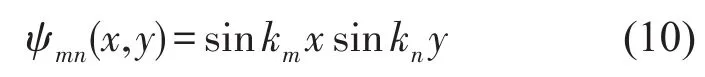
其中km=mπ/a,kn=nπ/b。结构受到外部激励作用时,将发生机械振动,进而向外压缩介质并辐射噪声。根据Rayleigh积分公式,平板表面声压可由其表面位移表示为

由于吸振器置于平板之上,将随平板一起振动,因此可将吸振器的振动位移写为

将式(9)、(11)、(12)代入式(8),将第二式两端乘以并沿平板表面积分可得


为Kww中的元素,根据矩阵K可求得耦合系统的固有频率,M、N分别表示在x、y轴方向上所取最大模态的序数。
得到声振耦合方程的解之后就可以根据式(11)求出平板的表面声压,进而求得平板的声辐射特性,利用结构振动表面声强积分可获得结构的辐射声功率,即有

其中T表示共轭转置,S为平板表面面积。结构表面法向振速均方值
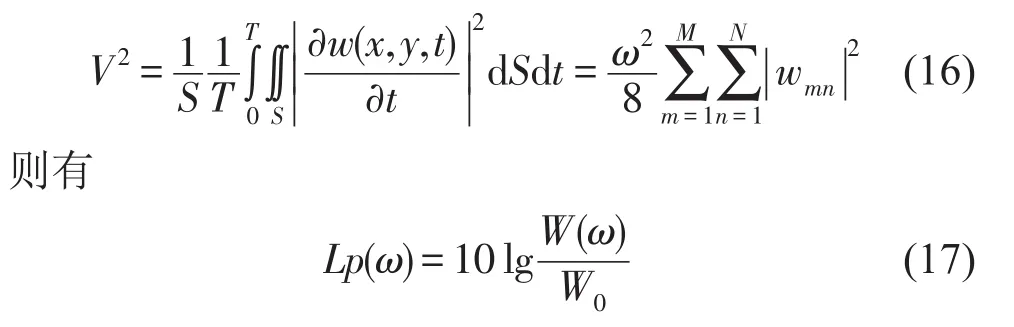
取参考声功率为W0=1×10-12W,参考振速为
3 声振特性优化
在结构表面布置动力吸振器的目的是为了改变结构表面的速度分布,进而控制结构的辐射声,使结构成为弱辐射体。下面利用遗传算法研究多个动力吸振器作用下平板结构声振特性的优化问题。以吸振器的结构参数和位置参数为优化变量,即

将目标函数选定为平板结构在一定频率范围内辐射声功率级和表面平均振速级的平均值J,即

其中S为频率范围内计算频率的总数,α、β为分配给辐射声功率级和表面平均振速级的权重系数,这里取α=0.5、β=0.5。遗传算法中,种群规模设定为200,迭代次数设定为300。
选择置于无限大声障板中的四边简支钢板为研究对象,钢板的参数为:长a=0.8 m,宽b=0.6 m,厚h=0.003 m;杨氏模量E=2.16×101(1N/m2),密度 ρ=7.85×10(3kg/m3),泊松比υ=0.3,根据研究对象的特性参数可给出优化变量的范围为

研究空气介质中,激励力幅值为1 N、作用点在(a/5,b/5)、激励频率范围在10 Hz~300 Hz内结构的声振特性,空气密度ρ0=1.293(kg/m3),声速c0=344(m/s)。表1给出了优化前后平均值J的变化情况,由表1知,优化前目标函数J=62.4 dB,采用一个吸振器优化后降低了18.7%,采用两个吸振器优化后J降低了26.0%,采用三个吸振器优化后J降低了27.0%。图2为优化前后频率范围在10 Hz~300 Hz内空气中平板的辐射声功率级和表面平均振速级,由图2知,优化后平板辐射声功率级和表面平均振速级曲线都得到了改善,共振频率向高频区偏移,频段内固有频率的数目也相对减少;动力吸振器对平板前几阶共振频率处峰值控制得比较明显;结合表1知,单个动力吸振器能够降低优化目标10 dB左右;增加吸振器个数可控制较高共振频率处的峰值,但对整个频段内平均值J的影响不大。

表1 空气中动力吸振器优化目标的结果
表2给出了空气中动力吸振器的优化结果,表3为平板前5×5阶固有频率的固有频率。单个吸振器优化时的阻尼振动频率 f1=528.3 Hz,与平板(1,5)、(2,5)、(4,4)阶固有频率接近。两个吸振器优化时的阻尼振动频率 f1=351.3Hz,与平板(1,4)、(2,4)、(4,3)、(5,2)阶固有频率接近;阻尼振动频率f2=488.6 Hz,与平板(4,3)阶固有频率接近。三个吸振器优化时的阻尼振动频率 f1=274.8 Hz,与平板(2,3)、(3,3)、(4,2)阶固有频率接近;阻尼振动频率f2=313.1 Hz,与平板(5,1)阶固有频率接近;阻尼振动频率 f3=352.9 Hz,与平板(1,4)、(2,4)、(4,3)、(5,2)阶固有频率接近。上述分析表明,在一定频率范围内采用动力吸振器优化平板的声振特性,吸振器的阻尼振动频率要与结构的高阶固有频率接近。采用多个吸振器时,吸振器的阻尼振动频率要在所选结构模态频率范围内合理分布。

表2 空气中动力吸振器参数的优化结果

表3 平板的前5×5阶固有频率(Hz)
研究水中激励力幅值为1 N、作用点在(a/5,b/ 5)、激励频率范围在10 Hz~300 Hz内平板声振特性的优化问题,水密度 ρ0=1 000(kg/m3),声速c0=1 500(m/s)。表4给出了优化前后平均值J的变化情况,采用单个吸振器优化后J降低了16.2%,采用两个吸振器后J降低了25.4%,采用三个吸振器后降低了27.6%。比较表1知,低阶共振频率处峰值控制的比较明显;单个动力吸振器能够降低优化目标10 dB左右,且单个吸振器对空气中结构声振特性的优化效果高于水中的;采用三个吸振器能够控制结构较宽频带的优化目标。图3为优化前后频率范围10 Hz~300 Hz内水中平板的辐射声功率级和表面平均振速级。由图3知,优化后平板辐射声功率级和表面平均振速级曲线都得到了改善,共振频率向高频区偏移,频段内固有频率的数目也相对减少;动力吸振器对平板前几阶共振频率处峰值控制得比较明显,增加吸振器个数可控制较高共振频率处的峰值,但对整个频段内平均值J的影响不大。比较图2知,水中平板结构的声辐射功率级和表面平均振速级比空气中大10 dB左右,因此在对水下结构进行声振优化时需考虑水介质的反作用。

表4 水中动力吸振器优化目标的结果

图2 优化前后空气中平板的声振特性

图3 优化前后水中平板的声振特性
表5给出了空气中动力吸振器的优化结果,单个吸振器优化时的阻尼振动频率 f1=491.1 Hz,与平板(4,4)、(5,3)阶固有频率接近。两个吸振器优化时的阻尼振动频率 f1=350.7 Hz,与平板(1,4)、(4,3)、(2,4)、(5,2)阶固有频率接近;阻尼振动频率f2=488.6 Hz,与平板(5,3)阶固有频率接近。三个吸振器优化时的阻尼振动频率 f1=365.4 Hz,与平板(1,4)、(5,2)、(2,4)、(4,3)阶固有频率接近;阻尼振动频率 f2=389.0 Hz,与平板(1,4)、(4,3)、(5,2)阶固有频率接近;阻尼振动频率 f3=488.5 Hz,与平板(5,3)阶固有频率接近。水中的优化结果和空气中的结果有明显区别,即不能直接将空气中的优化结果用于水中。

表5 水中吸振器参数的优化结果
4 结语
研究了考虑声振耦合效应时平板结构声振特性的优化问题。由Hamilton变分原理建立了多个动力吸振器-平板-介质系统的声振耦合方程,给出了简支边界条件下耦合系统的近似解;以动力吸振器的质量、刚度、阻尼和位置为设计变量,采用遗传算法对平板结构的表面平均振速级和辐射声功率级进行了优化研究。研究表明:
(1)由于动力吸振器能够与结构的振动耦合,改变了结构的固有频率,可以有效控制结构的振动与声辐射;
(2)动力吸振器能够有效降低结构低频段的振动与声辐射,对于较宽频段的振动与声辐射的控制,可采用多个动力吸振器;
(3)对于水下结构,仍可采用两个动力吸振器进行优化,但需考虑水介质的影响。
研究结果可为设计具有减振降噪效果的动力吸振器提供理论依据,也可为研究用非线性动力吸振器优化结构的声振特性奠定基础。
[1]Lang M A,Dym C L.Optimal acoustic design of sandwich Panels[J].Journal of the Acoustical Society of America,1975,57:1481-1487.
[2]Naghshineh K,Koopmann G H,Belegundu A.Material tailoring of structures to achieve a minimum radiation condition[J].Journal of the Acoustical Society of America,1992,92(1):841-855.
[3]Constans E W,Koopmann G H,Belegundu A D.The use of modal tailoring to minimize the radiated sound power of vibrating shells:theory and experiment[J].Journal of Sound and Vibration,1998,217(2):335-352.
[4]夏雪宝,向阳,吴绍维.基于波叠加法的结构声辐射形状优化研究[J].武汉理工大学学报,2014,36(1):94-98.
[5]杨恺,崔龙,黄海.主被动电磁式动力吸振器及其在桁架振动控制中的应用[J].振动与冲击,2012,31(18):14-19.
[6]孙朝晖,戴扬,孙进才.动力吸振器用于飞机壁板减振降噪的研究[J].西北工业大学学报,1993,14(10):B506-B507.
[7]Nagaya K,Li L.Control of sound noise radiated from a plate using dynamic absorbers under the optimization by neural network[J].Journal of Sound and Vibration, 1997,208(2):289-298.
[8]逯还通,陈克安,李双.基于辐射声功率最小化的安静结构设计[J].应用声学,2007,26(3):143-150.
[9]Li W L,Gibeling H J.An analytical solution for the self and mutual radiation resistance efficiency[J].Journal of Sound and Vibration,2001,245(1):1-16.
Vibro-acoustic Characteristic Optimization of Plates Considering Vibro-acoustic Coupling
ZHOU Qi-zheng,WANG De-shi,LI Yong-zhe
(Naval University of Engineering,Wuhan 430033,China)
The problem of vibro-acoustic characteristic optimization of a plate with dynamic vibration absorbers was investigated.The vibro-acoustic coupling equations of the absorber-plate-medium system were formulated based on Hamilton variational principle.The solutions of the coupling equations under simply-supported constraint condition were given by modal expansion method.Taking the mass,stiffness,damping and location of the vibration absorber as design variables,and the acoustic radiation power level and the surface quadratic velocity level as the objective,the plate-absorbers system was optimized by means of the genetic algorithm.The results reveal that a single dynamic vibration absorber can reduce the optimization objective by 10 dB in some frequency spectrum band,while using multiple vibration absorbers can control the noise in a wider spectrum band.For underwater structures,the optimization can be realized by using two absorbers.But the optimization results of the absorbers in the air cannot be used in the underwater structures directly.The results of this work can be used to design the dynamic vibration absorbers for vibration and noise control of structures.
vibration and wave;vibro-acoustic coupling;plate;dynamic vibration absorber;genetic algorithm; vibro-acoustic optimization
TB53
A
10.3969/j.issn.1006-1335.2015.03.019
1006-1355(2015)03-0087-05
2014-10-29
国家自然科学基金资助项目(11372350);海军工程大学博士创新基金资助项目
周奇郑(1985-),男,河南省邓州市人,博士生,主要研究方向:非线性振动、振动与噪声控制。E-mail:zqizheng@126.com。
王德石(1963-),男,博士生导师。
