建筑物出口的人员疏散研究1
2015-12-05赵士达
赵士达 张 楠 赵 颖
建筑物出口的人员疏散研究1
赵士达 张 楠 赵 颖
(天津市地震局,天津 300201)
根据建筑物出口疏散的特点,提出了一种改进型的元胞自动机模型。研究了影响人员疏散速度的两个因素:人员之间的相互拥挤产生的冲突和人员移动到出口时由于转弯导致的移动速度减慢。使用数学方法推导得出了摩擦冲突函数和转弯函数。通过计算机仿真与实际疏散实验对比发现,在不考虑转弯因素的情况下,仿真结果与实验结果偏差较大,而在同时考虑相互冲突和转弯因素时的仿真结果与实验结果偏差很小,验证了这两个因素是疏散仿真不可忽略的因素。通过分析仿真结果,验证了本文所采用的模型和函数能够准确地反映实际疏散过程,具有较高的实用价值。
元胞自动机 人群疏散 摩擦函数 转弯函数 疏散仿真
引言
随着社会的发展,人们对地震、火灾等突发事件越来越重视。为了减少人员伤亡和财产损失,各级地方政府先后制定了各种应对突发事件的应急预案。其中,制定人员疏散方案是应急预案的一项重点内容(赵士达等,2014),需要对人的运动行为进行系统研究。在过去的十几年里,各国学者对人员疏散行为进行了广泛深入的研究。其中人员疏散中的决策过程主要通过元胞自动机(Cellular Automata,CA)的规则进行演化并表现出来(朱刚等,2006;杨兆升等,2011)。自1966年由Von Neumann首次提出元胞自动机的概念以来,因为元胞自动机能将局部变化的反馈作用表现出来,并在模拟系统中具有较好的突变和自组织等特性,已被广泛应用于人群疏散、城市交通控制等领域(岳昊,2008)。为了减轻灾害发生时的损失,国内外诸多学者以CA模型为基础,从不同的角度对人员疏散过程进行了深入的研究,如:Heather等(2009)和Gong等(2000)将模糊规则引入到CA模型,建立了模糊元胞自动机(Fuzzy Cellular Automata,FCA)模型,并广泛应用于人员流动、城市发展等研究领域;朱艺等(2007)针对人口密度和出口条件对疏散过程进行了研究;张俊娜等(2012)将人工势能场与CA模型相结合,对人员疏散过程进行了研究。经过统计调查发现,在紧急情况下人员疏散时间主要花费在建筑物出口附近(Steffen等,2009)。所以,本文将对建筑物出口人员疏散进行研究。考虑到出口附近等待被疏散的人员通常是后排人与前排人交错排列,为此还对经典的二维元胞自动机空间模型进行了改进,并在此模型基础上分析了人之间的摩擦力和人运动到出口附近转弯对他人移动速度的影响。
1 改进的出口模型
经典的元胞自动机二维网格划分方法是将整个空间划分为若干个大小相等、整齐排列的正方形,它的冯·诺依曼型邻域如图1(a)所示。但是在人员疏散时,后排人为了获得更好的视野会选择交叉排列的方式,所以本文采用交叉式的网格划分方式,其邻域如图1(b)所示。从图1(b)可以看出,人会根据运动规律移动到其邻域元胞中,但是在实际疏散中出口附近的人不会选择后退,即不会向远离出口的方向运动。所以,本文对出口附近元胞自动机模型进行了改进,改进后的模型空间网格划分方式如图2所示。元胞E是紧邻出口的元胞,人需要经过元胞E到达出口。笔者将元胞1、2、3、4的人移动到元胞E的概率定义为∈[0,1],并将在一个时间步长内通过元胞E离开出口的概率定义为∈[0,1]。当元胞1、2、3、4只有1个人要进入元胞E时,该人进入元胞E的概率为1。当有2个或者2个以上人要进入元胞E时,就会产生冲突,即最多只有1个人可以进入元胞E,他人将保持在原来的位置不动。
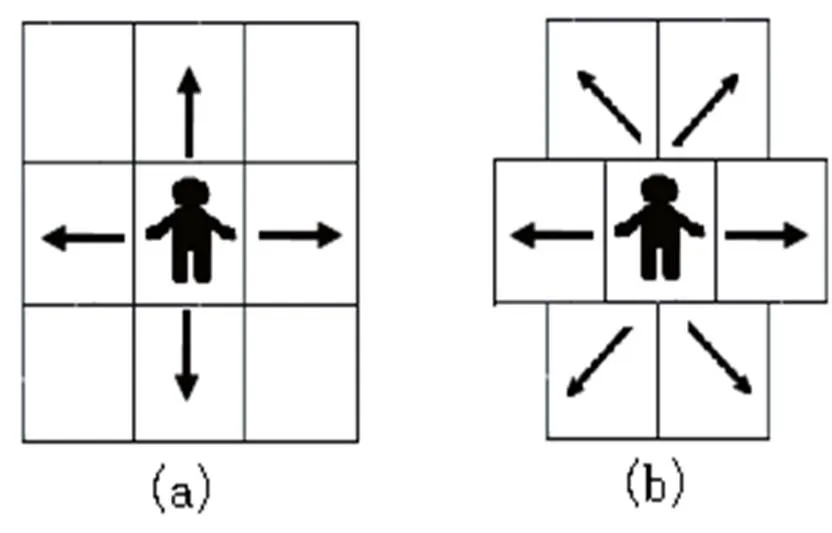
图1 整齐排列和交叉排列两种模型的邻域定义方式

图2 改进的出口模型
同时将全部人员保持在原来位置的概率定义为,那么人员成功移动到元胞E的概率就是1-。人员保持在原来位置的概率φ(k)可以用公式(1)来表示,其中k为同时向元胞E移动的人员数量。在下文中笔者将φ称为摩擦系数。
(1)
2 疏散人员之间的摩擦函数
通过公式(1)可以看出,在图2模型中当ke≥2时,摩擦系数是一个常量,它并不能反映出拥挤时人员之间的相互作用。所以本文引入摩擦函数ζ∈[0,1]。其中,ζ∈[0,1]表示在多个人员同时向同一个元胞移动时,不给其他人员让行的概率;摩擦函数ζ表示的物理意义是疏散时发生冲突并且冲突不能够解决的概率。这里,首先分析冲突发生时冲突被解决的两种情况:一是当冲突发生时,所有人员都选择保持在原来位置上给其他人让路,不存在多人竞争同一个位置的情况;二是只有一个人选择不给其他人让路,其他的人员选择保持在原来的位置不动,也不存在人员相互竞争的情况。摩擦函数的数学表达式如公式(2):
在公式(2)中,(1-ζ)k表示冲突发生时冲突被解决的第一种情况;kζ(1-ζ)k-1表示冲突被解决的第二种情况。由公式(2)可以得出:当k=1时,ζ=0;当k=∞时,ζ=1。其中,k=1时的物理意义是只有一个人试图移动到出口元胞时,不会发生冲突,移动到出口元胞的概率为1;k=∞时的物理意义是非常多的人试图同时移动到出口元胞时,冲突十分严重,几乎没有人能移动到出口元胞。从Daichi等(2007)的实验中可以看出,当k≥2时摩擦系数始终为常量,而摩擦函数随着k的增大而增大。这说明摩擦函数反映了不同k的阻塞强度。这里,笔者引用Daichi等(2007)的摩擦系数和摩擦函数随k变化的函数图,如图3所示。
图3 摩擦系数和摩擦函数随k改变的变化
Fig. 3 Values of the frictional parameter and the frictional function vs.e
从图3可以看出,摩擦函数随着k的增大而增大。同时从公式(2)也可以看出,摩擦函数的大小与产生冲突的人员数量有关,与元胞自动机网格划分方式无关。也就是说,本文所采用的摩擦函数不仅适用于本文所采用的元胞空间划分方式,而且也可以用于其它的元胞空间划分方式。
3 人员运动时的转弯函数
在疏散过程中人员的运动方向会随时发生变化。在每次运动方向发生变化时,人员会做出转弯的动作,这导致了人员的移动速度减慢。本文引入转弯函数用以表示行人在运动中由于转弯导致的减速效果,其数学表达式如公式(3):
(3)
其中θ∈[0,π]为人员移动转弯的角度。
例如在图2中,元胞1和4的人员先要移动到元胞E,再从元胞E移动到出口,这需要转弯90°,即θ=90°;元胞2和3的人员要移动到出口需要转弯30°。Η≥0为惯性系数,它反应人员惯性的大小。在本文第一部分提到了人员移动到元胞E的概率和在一个时间步长移动到出口的概率,这两个概率的关系可以通过一个简化的指数函数来表示(Ansgar等,2003),其数学表达式如公式(4):
(4)
由公式(4)可以看出,在一定时转弯的角度越大,人员移动速度降低的越快,离开出口的概率也就越小。
4 平均疏散速度
人员要移动到出口需要先移动到出口的邻域元胞,假设出口的邻域元胞个数为n,邻域元胞中同时想移动到出口元胞的人员个数为k。那么n个邻域中,k个人员试图移动到出口元胞的概率(k)如公式(5):
一个人成功移动到出口的概率就是k个人同时试图移动到出口并且冲突被解决的所有可能,因此,一个人成功移动到出口的概率(n)可以用公式(6)表示:
定义在时刻出口元胞没有被疏散人员占据的概率为π(0)和出口元胞被其邻域元胞中的人员占据的概率为π(),其中为出口元胞的第个邻域,那么在+1时刻,出口元胞的状态可以通过以下方程式表示:
(7)
在→∞时,通过方程式(7)可以推导出π∞()的数学表达式(8):
其中∈[1,n]。因为,所以由公式(7)和(8)可以得出π∞(0)的数学表达式(9):
假设出口宽度为一个元胞的宽度,那么一个步长时间内的平均疏散人数可以表示为:
(10)
5 计算机仿真与疏散实验
本文对人员疏散进行计算机仿真并与实际疏散仿真实验进行对比。在仿真中需要对18名人员按9种方式从建筑物中疏散。其中建筑物为长4m,宽3.5m的长方形,出口位于长边中央处,宽度为0.5m,9种疏散方式如图4所示。
在(H)和(I)两种疏散方式中人员可以自由移动,在其它疏散方式中人员按照图4中所示的方式移动。平均疏散人数可以通过以下公式计算得出:
(11)
式中,和分别表示第个被疏散的人员和第个被疏散的人员;t和t分别表示第个人员和第个人员被疏散的时刻。
在(A)到(D)的疏散方式中,仿真初期人员运动相对较快,出口附近没有冲突,计算平均疏散人数时要等人员运动状态稳定后进行计算,所以本文取=5,=18。在(E)到(I)的疏散方式中,疏散末期出口附近人员数量减少,人员移动速度相对较快,在计算平均疏散人数时不应包括疏散末期,所以本文取=1,=14。
对这9种疏散方式分别进行2次仿真。在第一次仿真时,只考虑人员之间的摩擦力作用,不考虑转弯对疏散的影响,可计算得到平均疏散人数
通过计算机仿真结果和实际试验结果综合分型,笔者得出了以下几点结论:
(1)对比(B)、(E)和(G)三种疏散方式可以发现,随着n(n≥2)的增大,出口附近发生冲突也越严重,疏散速度也越慢。
(2)当n一定时,在不考虑转弯函数的仿真时,(B)、(C)和(D)三种疏散方式的仿真疏散速度基本相同,但其仿真速度与实际试验的速度相差较大;在考虑转弯函数的仿真和实际试验时,(B)、(C)和(D)三种疏散方式的仿真疏散速度随着θ增大而降低,与实际试验的疏散速度相差不大,验证了转弯过程对人员疏散的减速效果。
(3)观察(G)、(H)和(I)三种疏散方式发现,其疏散速度非常相似。这是因为(H)和(I)两种疏散方式在人员之间会自由运动,当达到稳定状态时人员之间会分别占据出口的4个邻域,其疏散方式与(G)类似。
(4)通过图5可以发现,
(5)仿真中
6 结论与展望
根据建筑物出口人员疏散的特点,本文提出了一种改进型的元胞自动机空间划分模型。介绍了影响人员疏散速度的两个函数:摩擦函数和转弯函数。根据数学理论推导得出了相关函数的数学表达式。同时,使用文中的数学公式和相关参数对人员疏散进行了计算机仿真,分别得出了考虑转弯因素和不考虑转弯因素的人员疏散时间,并将这一仿真结果与Daichi等(2009)的疏散实验结果进行了对比。通过对比发现,考虑转弯函数的仿真结果与实际疏散结果更接近,更能充分地反映人员的疏散过程。
杨兆升,高学英,孙迪,2011. 城市交通疏散救援的元胞自动机模型. 交通运输工程学报, 2(4):114—120.
岳昊,2008. 基于元胞自动机的行人流仿真模型研究. 北京:北京交通大学, 14—25.
张俊娜,范海菊,2012. 基于人工势场和Agent的人员疏散系统仿真. 计算机应用,32(6):1753—1756.
赵士达,张楠,杨爽,2014. 基于Android系统的避难场所查询软件开发. 电子技术应用,40(3):133—136.
朱刚,马良,2006. 基于元胞自动机的物流系统选址模型. 上海理工大学学报,(1):19—22.
朱艺,杨立中,李健,2007. 不同房间结构下人员疏散的CA模拟研究. 火灾科学,16(3):175—179.
Steffen B., Seyfried A., 2009. Methods for measuring pedestrian density, flow, speed and direction with minimal scatter. Physica A: Statistical Mechanics and its Applications, (12): 015.
Kirchen A., Nishinani K., Schadschneider A., 2003. Friction effects and clogging in a cellular automaton model for pedestrian dynamics. Physical Review E-PHYS REVE, 67: 056122.
Yanagisawa D., Nishinar K., 2007a. Mean-field theory for pedestrian outflow through an exit. Physical Review E-PHYS REVE, 76 (6): 75-80.
Yanagisawa D., Kimuna A., 2009b. Analysis on Pedestrian Outflow through an Exit with an Obstacle. ICROS-SICE International Joint Conference, 8: 5040—5045.
Gong Q.L., Mendel J.M., 2000. Interval type-2 fuzzy logic systems: theory and design. IEEE Transactions on Fuzzy Systems, 8 (5): 535—550.
Heather Betel, Paola Flocchini, 2009. On the asymptoti behavior of fuzzy cellular Automata. Electronic Notes in Theoretical Computer Science, 252: 23—40.
Yushi Suma, Daichi Yanagisawa., Katsuhiro Nishinari, 2012. Anticipation effect in pedestrian dynamics: Modeling and experiments. Physica A: Statistical Mechanics and its Applications, 391 (1): 248—263.
Research on the Safe Evacuation near the Building Exit
Zhao Shida, Zhang Nan and Zhao Ying
(Tianjin Seismological Bureau, Tianjin 300201, China)
The paper presents an improved cellular automaton model according to the feature ofevacuation near the outlet. We studied friction and turning factors that affect pedestrian evacuation speed, and derived expression offriction function and turning function by using mathematical methods. The average pedestrian outflow of the simulation that includes the effects of both the frictional function and the turning function agrees well with experiment result. In contrast, the simulation results that only include the effect of the frictional function are not corresponding to the experimental ones well. Simulation results show that friction and turning should not be ignored. By analyzing the simulation results, we verified that the model can accurately reflect the actual evacuation process and has practical value.
Cellular automaton; Pedestrian evacuation; Friction function; Turning function; Evacuation simulation
天津市地震局青年基金项目(121010)
2014-07-30
赵士达,男,生于1983年。工程师。主要研究方向:地震应急指挥、地震现场通讯和灾害评估。E-mail:zhaoshida@163.com
