工科院校《概率论与数理统计》课程的教学改革与探讨
2015-12-04张金凤
张金凤
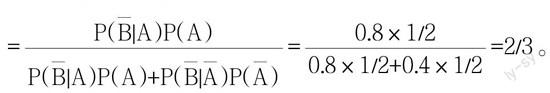
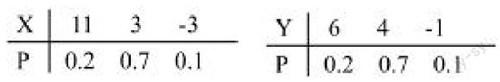
摘要:本文分析了概率论与数理统计课程的教学现状,针对现状提出了从案例教学、实验教学、与专业相结合、建设网络教学平台等几个方面进行改进,并适当地让学生参与到教学环节中,达到激发学生的学习积极性和主动性,提高教学效果的目的。
关键词:《概率论与数理统计》;案例教学;实验教學;网络教学平台
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2015)18-0085-02
《概率论与数理统计》是继《高等数学》、《线性代数》之后,理工、经管等专业必修的公共基础课程,对培养学生处理“随机”的数学基础知识、基本能力和综合素质具有其他课程不可替代的作用。本文考虑到笔者所在学校学生的实际水平以及在教学过程中存在的一些问题,结合笔者多年的教学经验,对《概率论与数理统计》课程从案例教学、实验教学、网络教学平台几方面进行探讨,仅供各位同仁参考。
一、目前教学现状
笔者根据多年的《概率论与数理统计》教学经验对目前教学中普遍存在的一些问题进行总结,主要有四个方面:(1)教学内容一成不变,一本教材多专业通用,例题与练习不能很好地结合学生专业特点,致使学生不了解《概率论与数理统计》对后续课程以及专业课的影响和作用,学习时缺乏热情和主动性。(2)教学手段单一,大多采用板书+多媒体课件的形式。一些教师过度依赖多媒体课件,虽然缓解了教师书写的压力,但由于形式过于呆板,课件内容固定,教师不能灵活地调整教学内容,学生处于被动的听课状态。(3)现有相关教材多注重概率统计的理论,而对如何操作软件来解决实际问题介绍得很少。由于学时有限,教师也将精力主要放在理论内容的讲解和计算上,使得学生对课程的理解停留在理论层面上,造成课程理论与实践相脱节。(4)理工科的《概率论与数理统计》多以45学时为主,课程安排一般为两周三次课,时间安排不够紧凑。学生在课后对课上的内容只能凭记忆进行总结和消化吸收,如果不能及时复习内容,就会造成知识的积压,影响后面的学习。面对以上教学中存在的问题,如何有效地提高课堂的教学效果,激发学生的学习主动性,是教师面临的亟待解决的问题。
二、改善教学效果的几点建议
1.将案例教学融入课堂,激发学生的学习兴趣。由于概率论与数理统计的实用性强,生活中的许多现象均可运用概率统计的知识和方法来解释。教师在讲授某个知识点时,不妨将相关的生活实例融进教学中,激发学生学习的兴趣,使得抽象的定义、公式更为直接易懂,有助于学生对知识点的理解和掌握。比如在介绍贝叶斯公式时,可借用一个大家耳熟能详的“狼来了”的故事来理解和体会贝叶斯公式。故事讲的是一个放羊的小孩,在两次欺骗村民说“狼来了”后,第三次狼真来了,而没人相信的事。接下来利用贝叶斯公式进行分析。设事件A表示小孩说谎话,事件B表示狼来了。先做一些假设:村民对小孩的信任程度一般,即P(A)=P(■)=1/2,而说谎的小孩喊狼来了的概率P(B|A)=0.2,说真话的小孩喊狼来了的概率P(B|■)=0.6。那么当小孩第一次说谎喊狼来了的时候,村民对小孩说谎的印象P(A|B)由贝叶斯公式计算得:P(A|■)=■=■=2/3。这时注意到村民对小孩的说谎的概率由0.5上升到0.667,可记P(A)=2/3,P(■)=1/3。小孩第二次说谎喊狼来了的时候再次利用贝叶斯公式得P(A|■)=0.8。通过以上的计算表明,在村民上过两次当后,对小孩说谎话的概率已经由0.5修正到0.8,面对如此高的说谎概率,试问村民听到第三次小孩喊狼来了,怎么还会去上山呢?可见人与人之间的信任禁不起谎言的消磨。对生活中一个大家都熟识的寓言,通过全概率公式的分析,将结论量化,更容易理解。再比如讲解数学期望这个重要的概念时,可以将期望概念的起源故事即“赌资分配问题”介绍给学生。所谓的“赌资分配问题”是17世纪中期一位赌徒向数学家帕斯卡提出了一个困扰他很久的问题:甲乙两赌徒相约,利用掷硬币的方式进行赌博,各出50法郎,谁先赢三局即可得全部赌本100法郎。当甲赢了两次,而乙只赢一次时,因事需终止赌博,那么赌金如何分配呢?当这个问题在课堂上提出时,不少学生产生了兴趣,并给出了自己认为合理的答案,这时教师进而引出正确的解法。1654年帕斯加提出最多只需再玩两次就可结束此次赌博,这两次可能出现的结果分别为:甲甲、甲乙、乙甲、乙乙。对于甲来说只要出现四种可能结果的前三种,甲都胜出,故甲得100法郎的概率是3/4,得到0法郎的概率为1/4,从而甲应期望得到100×3/4+0×1/4=75法郎。其意指,若再继续此种赌博多次,甲每次平均可得75法郎。从这个解法中引出数学期望的概念即E(X)=x1p1+x2p2。除引用有趣的案例外,教师还可以尽可能地让学生参与到教学环节中,以激发学生学习的积极性和主动性。
2.让实验教学走入课堂,提高学生实际动手操作的能力。《概率论与数理统计》是一门应用性、实践性很强的学科,其在各方面的应用性可以通过例题呈现给学生,而实践性在现有的教学环节中并没有得到充分的体现,学生不能利用所学的知识解决一些简单的概率统计问题。教师在课堂上可以选择一些题目进行简单的操作,向学生展示概率计算和统计分析的基本步骤。课后提供相应的练习,促使学生在学习中较自然地掌握计算机的实现过程,较好地解决了实践与教学相脱节的问题。
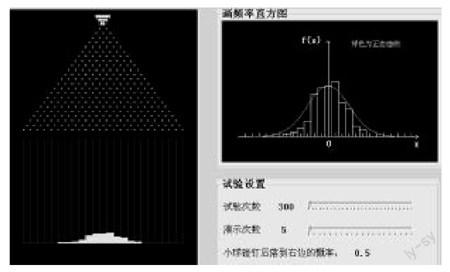
3.充分利用现代化教学手段,提高课堂教学效果。课堂教学多采用板书+多媒体课件的形式,在以教学效果为主的前提下,二者可以相互补充,扬长避短。无论是板书还是多媒体课件的使用,都要有个度,比如定理的推导和例题的计算,适合用板书来讲解,达到师生互动的良好效果。而定义、定理的陈述、图形的演示可以利用多媒体,一方面省去教师书写的压力,另一方面借助多媒体展示图形能更好地理解问题。此外也可以考虑将一些现代化的教学手段和成果穿插在教学中,一定程度上可以提高教学效果。比如在介绍独立同分布的中心极限定理时,不妨先借助著名的高尔顿钉板试验,通过不断地调整试验次数和演示次数,将小球堆积的效果图与正态分布曲线相比较,从而分析引出中心极限定理内容,可以帮助学生更形象、直观地理解中心极限定理的思想。
4.结合专业特点,精选例题。为了更好地将《概率论与数理统计》课程与学生专业相结合,教师可以根据所教学生专业的特点,选择和专业贴合较近的例题,这样学生在学习时,能较好地了解该课程对后续专业课的影响和作用。比如给金融、经济专业的学生上课时,关于数学期望和方差的概念,不妨可以通过一个关于风险投资的问题来理解。例题:某人有一笔资金,可投入两个项目:房地产和开商店。其收益都与市场状态有关。若把未来市场划分为好、中、差三个等级,其发生的概率分别为0.2、0.7、0.1。通过调查,该人认为购置房地产的收益X和开商店的收益Y的分布如下表,問该人资金应该流向何方?
先计算数学期望(即平均收益)E(X)=4(万元),E(Y)=3.9(万元)。从平均收益看,购置房地产利益比开商店多0.1万元。再计算两者的方差,D(X)=15.4,D(Y)=3.29。方差越大,收益的波动越大,从而风险就越大,显然购置房地产的风险要比开商店大得多。综合考虑,该投资者还是选择开商店。
5.建立网络教学平台,引导学生自主学习。网上资源丰富,但学生想找到合适的内容就不太简单,而且还要花费大量的时间。所以笔者依托学校提供的平台建设适合各阶段学生的网络教学平台。网络教学平台包含教师精心选取的内容,既可以节省学生的时间,又可以有针对性地引导学生自主学习。网络教学平台主要包括概率统计的各章课件、校级教改成果-概率论与数理统计习题课视频、各章节知识点总结、各章习题答案、历年期末试题、考研辅导材料以及国内一些大学历年期末试题几个模块。其中概率论与数理统计习题课的视频可供学生随时观看,作为课堂教学的补充,而且该形式不受时间、地点的限制,从而将学生由被动的课上学习转化为课下的主动学习,解决了课下每周仅有一次答疑时间的局限性,学生可以根据针对个人情况有选择地学习。《概率论与数理统计》网络教学平台的建立,较全面、完整地将《概率论与数理统计》课程组织在一起,使学生在利用平台学习时,根据自身学习情况,有针对性地选择,并辅以习题来巩固和提高理论知识,通过试卷检验自己的学习效果。
三、结论
本文对《概率论与数理统计》课程的教学现状进行分析,从案例教学、实验教学、网络实验平台等几个方面进行相应的改善,教学效果在一定程度上得到了提高,同时了也激发了学生的学习积极性。当然,教学改革是无止境的,要根据学生层次、教学内容等不断地进行调整,以达到较好的教学效果。
参考文献:
[1]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004.
[2]朱淑芹,班朝磊.《概率论与数理统计》教学改革探讨[J].教育教学论坛,2014,(45).
[3]张瑞亭.对概率统计教学中若干问题的探讨[J].教育教学论坛,2014,(02).
