基于损伤塑性模型的无腹筋简支梁的非线性分析

张庭杰，贾朋涛

(重庆交通大学土木建筑学院，重庆400074)

钢筋混凝土是土木工程应用最广的材料，也是一种力学性能复杂的非匀质材料。由于其不同于一般的弹塑性材料，使得模拟计算结果与实际相差较大。不少学者采用通用大型有限元软件实现了单调荷载下钢筋混凝土梁三维非线性有限元分析［1－6］。目前，采用三维有限元法难以实现基于混凝土损伤塑性模型的钢筋混凝土梁非线性有限元分析，关键原因是难以合理确定混凝土材料真实的本构关系。为此，本文采用ABAQUS提供的依据Lee and Fenves和Lubliner提出的混凝土损伤塑性模型，应用ABAQUS/Standard 6.12有限元分析软件，对剪跨比为1.5的无腹筋简支梁进行了精细的非线性有限元建模计算和探讨，并与实验结果进行了对比。此模型是基于文献［7］的工作上，采用混凝土损伤塑性模型对无腹筋简支梁的破坏过程进行非线性有限元分析。

1 混凝土损伤塑性理论

导致混凝土非线性特征的主要原因是混凝土微裂缝的产生、发展和集结，要详细考虑混凝土材料性能的劣化过程，仅仅用一般的材料塑性理论不能真实地反映混凝土材料的本构特性，而连续介质损伤力学(CDM)理论在发展这种材料的本构关系中提供了新的理论框架，因此建立混凝土的损伤塑性模型成为对混凝土结构进行非线性有限元分析的重要方法之一［8-10］。

混凝土在非线性阶段既有存在刚度退化又有塑性变形，在细观上表现为与材料变形细观机理相联系的滑移与流动和裂缝、缺陷的扩展［5］。正确的混凝土本构关系应该可以反映塑性变形和塑性损伤两种机制的塑性损伤本构。为了避免陷入分析材料微细结构的麻烦之中，一般都将混凝土作为宏观各向同性材料而对它的变形和失效机理进行研究［8］。ABAQUS采用的混凝土损伤塑性模型(见图1)是在Lee and Fenves［11］和Lubliner［12］提出的模型基础上建立的，该模型为连续的、基于塑性的混凝土损伤模型。它假定混凝土材料主要因拉伸开裂和压缩破碎而破坏。屈服或破坏面的演化由拉伸和压缩等效塑性应变这两个硬化变量来控制。它基于以上的假设条件，适用于混凝土在任意荷载情况下的受力，包括循环荷载，同时考虑了由于拉压塑性应变导致的弹性刚度的退化以及循环荷载作用下的刚度恢复。

ABAQUS在分析混凝土材料上有很强的能力。它提供了三种混凝土塑性本构模型:混凝土损伤塑性(concrete damaged plasticity)模型，混凝土弥散开裂(smeared cracking)模型和ABAQUS/Explicit的混凝土开裂模型。本文采用ABAQUS提供的依据Lee and Fenves和Lubliner提出的混凝土损伤塑性模型，该模型的计算结果与实际符合较好，适合模拟混凝土的损伤本构关系［11-12］。

2 ABAQUS中试验梁材料参数的定义

2.1 混凝土损伤塑性参数的定义

本次试验数据是采用C30的混凝土材料进行的，ABAQUS中混凝土损伤塑性的数据采用C30混凝土的本构关系计算的损伤数据。混凝土损伤数据的定义采用如图2、图3所示的曲线取值，本文采用精度较高的高斯积分方法通过Matlab编程求得∫f(ε)dε，再由式(1)求得混凝土受压、拉的损伤因子 dc、t。其中E0、f(ε)由采用的混凝土本构关系曲线模型确定，E0为混凝土的初始弹性模量，f(ε)为混凝土本构关系曲线中用ε表示的应力σ的函数。dc、t的计算结果如表1所示。其他参数的取值见表2所示。混凝土和钢筋分别采用C3D8R单元和T3D2单元进行分离式建模，并采用Embedded技术进行自由度耦合。

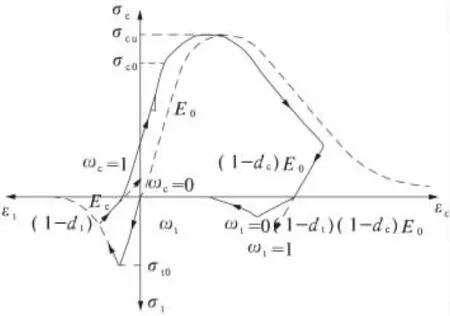
图1 ABAQUS采用的混凝土损伤塑性模型

图2 混凝土损伤塑性模型受压应力—应变关系

图3 混凝土损伤塑性模型受拉应力—应变关系

2.2 钢筋的本构关系

受拉主筋的屈服点为335 MPa，此时对应的非弹性应变为0，当应力为355 MPa时，塑性应变εpl为0.01。

表1 C30混凝土损伤因子的取值表

表2 C30混凝土损伤塑性参数的取值表

3 试验结果与有限元分析结果的对比与分析

3.1 概述

本实验采用的是剪跨比为1.5的无腹筋简支梁，简支梁的截面尺寸为250 mm×500 mm，剪跨段长度取700 mm，只配有3φ16受拉筋，试验梁属于适筋梁。试验中混凝土采用强度等级为C30的商品混凝土。试验梁的编号采用L1。为方便裂缝发展过程的描述，将构件划分为Ⅰ、Ⅱ、Ⅲ三个区段(Ⅰ、Ⅲ区为剪跨段、Ⅱ区为纯弯段)(见图4)。

图4 试验梁的配筋与加载位置示意图

3.2 有限元分析与试验结果对比

整个试验过程采用一次性加载至破坏，试验过程中的试验结果和现象均详细记录，限篇幅有限，只列出整个试验过程的几个典型的阶段进行实验结果与有限元分析结果的对比，将对比结果列于图5～图9。有限元模拟采用的是位移加载，有利于计算收敛，加载位移为45 mm，在加载的垫块上方耦合(coupling)一个参考点，作为位移加载点和支反力的查看。从试验最终的破坏形态可以看出加载过程中荷载施加的稍微有些偏载，但不影响整个试验的效果，试验梁最终的破坏形态见图10。

(1)当P=120 kN时，构件纯弯段首先出现弯曲裂缝;Ⅱ区W侧加载点下首先出现弯曲裂缝b1，裂缝开展高度约160 mm，角度约90°。首条裂缝出现的区域和发展的方向有限元计算的结果与试验结果吻合较好，首条裂缝出现的具体位置和长度有差异。有限元模拟不出实际的裂缝，但损伤情况与实际符合较好(见图5)。

图5 P=120 kN时，构件试验结果与有限元分析对比

(2)当P=140 kN时，构件弯剪段出现弯剪斜裂缝;Ⅰ区距W侧加载点约230 mm处开裂，高度约55 mm，此条裂缝在后来随着荷载的增加发展为弯剪斜裂缝a3。此时有限元计算的损伤出现位置与试验符合较好(见图6)。

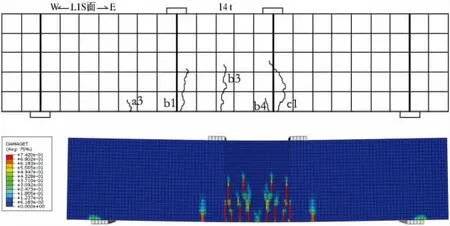
图6 P=140 kN时，构件试验结果与有限元分析对比

(3)当P=240 kN时，腹剪斜裂缝出现，有限元结果与试验结果吻合较好(见图7)。

(4)当P=340 kN时，Ⅰ、Ⅲ区斜裂缝和Ⅱ区直裂缝继续向支座处发展，此时，试验梁上缘混凝土还没有被压碎，钢筋也没有屈服，试验梁还可以继续承载，此时有限元计算结果与Ⅱ区直裂缝符合较好，但在剪弯区，斜裂缝模拟的效果不是很好(见图8)。

(5)当P=420 kN时，构件弯曲破坏。腹剪裂缝a1最大宽度达到20 mm，钢筋屈服，梁上部混凝土被压碎，大块混凝土剥落。本级荷载下构件跨中挠度达到43 mm，加载点挠度达到40 mm，无法继续持荷，发生弯曲破坏。有限元计算结果除了弯剪区斜裂缝计算有差异，其他位置裂缝与试验结果吻合较好。有限元模拟到加载点的挠度为45 mm，最后的结果收敛(见图9)。

图7 P=240 kN时，构件试验结果与有限元分析对比

图8 P=340 kN时，构件试验结果与有限元分析对比

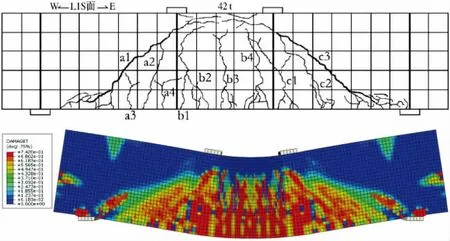
图9 P=420 kN时:构件试验结果与有限元分析对比

图10为试验梁的最终破坏形态，通过剪跨比为1.5的无腹筋简支梁加载试验的结果看出，裂缝首先出现在纯弯段，竖直向上发展，随着荷载的增加，弯剪区斜裂缝也出现，从梁底部向加载位置发展，最终的破坏属于受弯破坏。采用ABAQUS中的混凝土损伤塑性模型对该试验梁进行非线性分析，分析结果与试验结果基本吻合。

图10 试验梁的最终破坏形态

4 结论

根据试验结果，本文对剪跨比为1.5的无腹筋简支梁进行了非线性有限元分析。分析结果表明，有限元模型合理，与试验结果吻合良好，可以得到以下结论:

(1)混凝土损伤塑性，区别于一般的材料非线性本构关系，以混凝土受压破碎和受拉开裂为准则。通过损伤塑性模型的有限元计算结果与试验结果对比，可知用ABAQUS中混凝土的损伤塑性模型模拟混凝土材料的非线性本构关系是行之有效的。

(2)由于混凝土材料的特殊性，损伤塑性模型参数的取值对于计算是否收敛起到很大的作用 。对于混凝土的粘滞系数、膨胀角等，都值得反复推敲，其中粘滞系数取0.000 5，膨胀角取30°时计算容易收敛也与实际符合较好，有限元模拟建议采用位移加载，混凝土损伤塑性(concrete damaged plasticity)模型比弥散开裂(smeared cracking)模型容易收敛。

(3)混凝土损伤塑性模型模拟的弯剪区段的裂缝与实际吻合不是很好，说明混凝土损伤塑性模型包括参数的选择还有待改进。

(4)混凝土损伤塑性模型能较好地预测钢筋混凝土构件的抗弯和抗剪性能及其破坏特征。

［1］ 沈聚敏，王传志，江见鲸.钢筋混凝土有限元与板壳极限分析［M］.北京:清华大学出版社，1993.

［2］ 吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性有限元理论与应用［M］.上海:同济大学出版社，1997.

［3］ 董哲仁.钢筋混凝土非线性有限元法原理与应用［M］.北京:中国铁道出版社，1993.

［5］ 何政，欧进萍.钢筋混凝土结构非线性分析［M］.哈尔滨:哈尔滨工业大学出版社，2006.

［6］ 孔丹丹，赵颖华，王萍，等.钢筋混凝土材料有限元分析中的等效模量方法［J］.沈阳建筑大学学报:自然科学版，2005，121(13):200 －203.

［7］ 蒋宁.剪跨比为1.5的无腹筋简支梁受剪性能试验研究及有限元分析［D］.重庆:重庆大学，2005.

［8］ Frank J.Vecchio，Michael P.Collins.Predicting the response of reinforced concrete beams subject to shear using modified compression field theory［J］.ACI Structural Journal，1988:85(3):258 － 268.

［9］ 江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京:清华大学出版社，2005.

［10］ 李杰，吴建营，陈建兵.混凝土随机损伤力学［M］.北京:科学出版社，2014.

［11］ Lee J，Fenves G L.Plastic-damage model for cyclicloadingof concrete structures［J］.Journal of Engineering Mechanics，1998，124(8):892 －900.

［12］ Lubliner J，Oliver J，Oller S，et al.A Plastic damage model for concrete［J］.International Journal of Solids and Structures，1989，25(3):299 －326.