基于振动模态的振动筛横梁裂纹损伤机理

朱 艳，李曙生，曹元军

（泰州职业技术学院 机电学院，泰州225300）

国家中长期科学和技术发展规划纲要（2006－2020年）把产品制造过程中的在线检测与评估技术列为重要研究方向。很多结构物的损伤大多为板、梁的裂纹，对大型复杂结构，刚开始时因裂纹微小而不易被发现，但随着连续工作时间以及工作强度的增大，裂纹的扩展往往会导致严重的灾难性事故。

裂纹是最常见的一种结构损伤形式，对裂纹进行在线监测，可以经济可靠地保证结构使用安全，具有重要意义。裂纹的无损检测主要有振动检测法、声发射法、漏磁检测法、红外检测法、光学检测法、涡流检测法等，其中基于结构动力学的振动诊断法易于提取信号，实现检测自动化，适用于运行状态下的在线检测。

郑渝［1］在基于振动筛的振动特性及其结构损伤的研究中，提出了振动筛子结构损伤定位方法。李建忠等［2］将超声衍射时差检测技术应用于不锈钢焊缝的检测中，利用小波包分解技术对检测信号深入分析，获得缺陷信号和噪声信号在时频域上的分布特征。刘贵杰等［3］将小波分配尺度谱和小波能量系数应用于海洋结构件的典型疲劳裂纹扩展和断裂声发射信号的特征提取中，运用PXWAE 声发射检测仪对试件断裂全过程进行监测，成功提取到裂纹扩展和断裂过程中的声发射信号。DOUKA 等［4］等对含有单裂纹和双裂纹的悬臂梁进行了裂纹位置及裂纹深度的研究，并提取出悬臂梁振动的位移模态作为小波分析的原始信号。

基于上述研究，笔者以矿用振动筛的横梁为研究对象，从理论上建立了损伤梁的模型，并通过改进后的Ritz级数法计算了有裂纹简支梁的固有频率及振型。基于模态参数的变化，提出识别裂纹梁中裂纹位置的能量密度法以及识别裂纹梁损伤程度的神经网络法。最后通过对裂纹简支梁进行试验模态分析并验证了识别方法的有效性。

1 裂纹简支梁固有频率及其振型的Ritz解法

1.1 Ritz级数法运动方程求解裂纹简支梁的理论基础

设梁单元的损伤只引起单元刚度的下降而不引起单元质量的损失，可以首先将损伤梁划分成适当的单元。

设横向变形随时间按简谐规律变化，即w（x，t）＝W（x）cosωt，则梁的最大动能可以表示为：

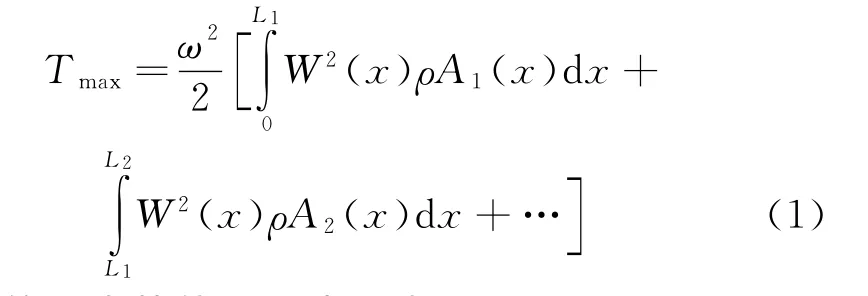
梁的最大势能可以表示为：

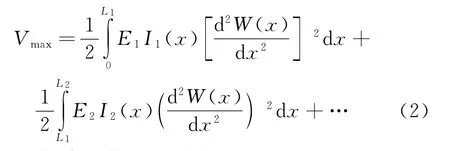
从而损失梁的Ritz商为：

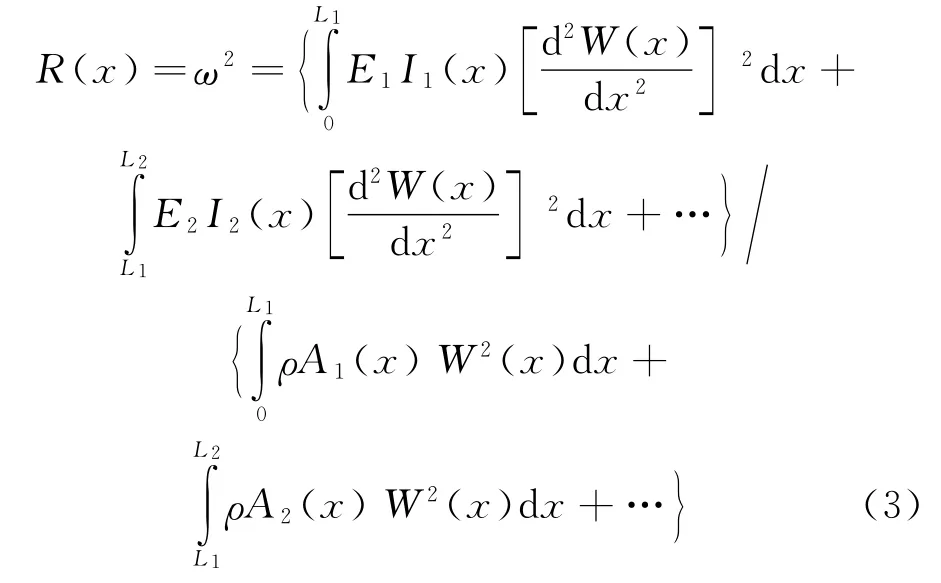
式中：ρ为材料密度；A为截面面积；Ei，Ii，Ai，Li为单元（i＝1，2，…）的弹性模量、横截面的惯性矩、横截面面积和长度；W（x）为梁的最大横向变形量。

则对于模态振型，只需求出损失梁单元对应的惯性系数和刚度系数，即

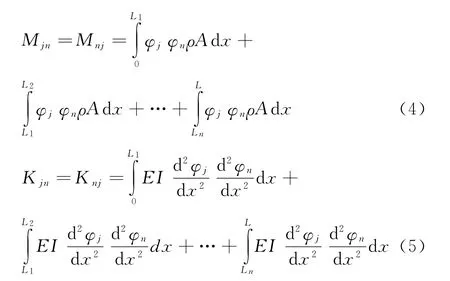
式中：n为梁分成的单元数；M为惯性系数；K为刚度系数。

1.2 固有频率及振型计算

假设简支梁的长为0.635 m，宽为0.015 m，高为0.01m，这里简支梁的数据与试验中的简支梁尺寸是一致的。

将简支梁沿着长度方向平均分成十个单元，如图1所示。假设梁的损伤只会引起梁单元的刚度发生变化而不会改变梁单元的质量，以梁单元刚度的变化作为识别损伤梁的损伤因子，应用Ritz级数法，利用MATLAB软件［5］编制相应的程序，就可计算出相应的梁单元出现损伤时，其损伤梁的前五阶固有频率及其振型。

图1 简支梁的有限元划分模型

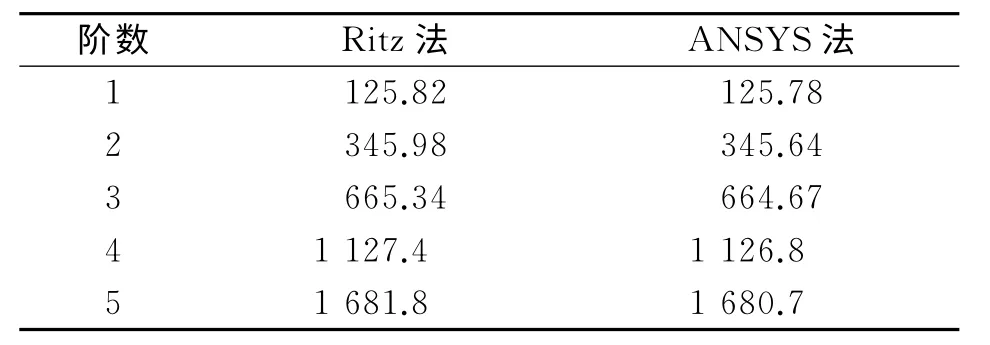
表1 Ritz法与ANSYS法计算固有频率比较 Hz

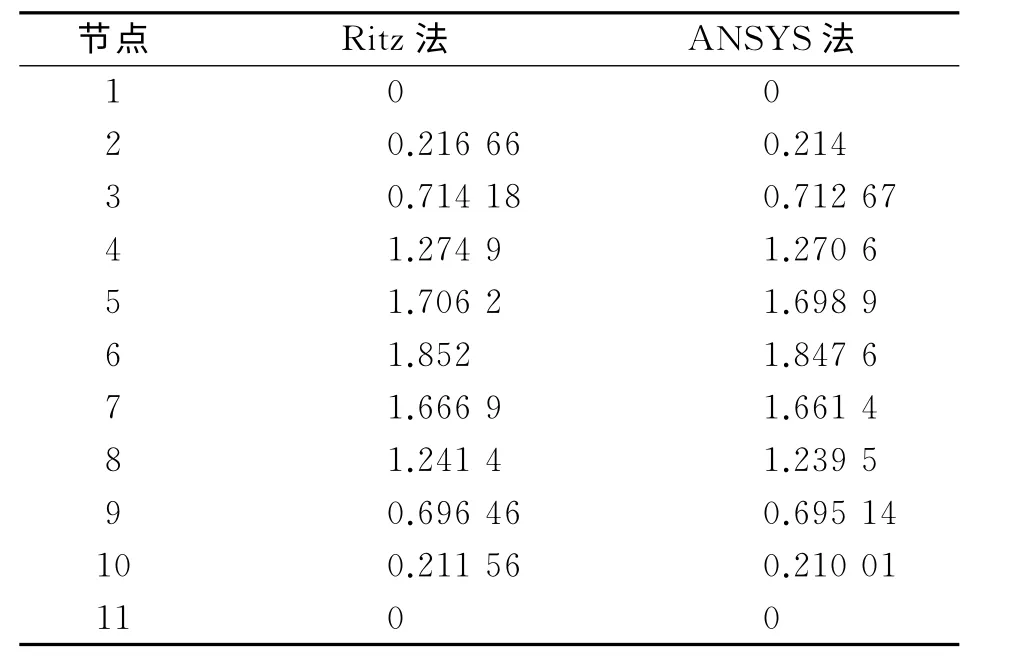
表2 Ritz法与ANSYS法计算第一阶模态比较 Hz

根据表1，2可以看出，将用改进后的Ritz级数方法计算得到的固有频率和振型数据和用ANSYS软件模拟得到的固有频率和振型数据对比可以发现，两种方法得到的模态数据非常吻合，从而验证了改进后Ritz级数法对裂纹梁处理方法的正确性。

2 裂纹简支梁损伤识别

利用基于ANSYS提取出来的数据进行裂纹简支梁的损伤识别，损伤识别分析是基于MATLAB软件编程计算以及绘图进行的，并分析几种损伤识别的方法。

2.1 基于ANSYS提取裂纹简支梁模态数据

在用有限元法分析计算时，分别只在梁上相对位 置0.1，0.2，0.3，0.4，0.5，0.6 处开不同深度的裂纹，裂纹的相对深度从0.1，0.2，0.3，0.4，0.5，0.6变化。可以得到梁在不同位置不同深度裂纹下各阶固有频率的变化，从而可以分析出来裂纹对梁的固有频率的影响。第一阶固有频率的变化率随裂纹位置和深度的分布如图2所示。

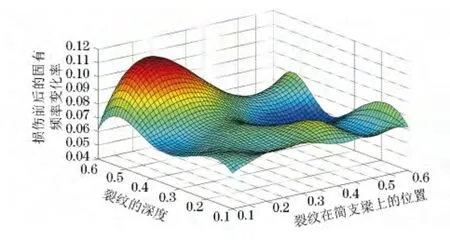
图2 第一阶固有频率的变化率随裂纹位置和深度的分布

同时对简支梁网格划分时，依次选取了其中120个均匀分布的点，根据这120个点的振型参数，计算不同点处在含有裂纹和不含裂纹时的振型之差值，分析裂纹从在梁中10%的位置到60%的位置时振型差值的变化图（图3）。

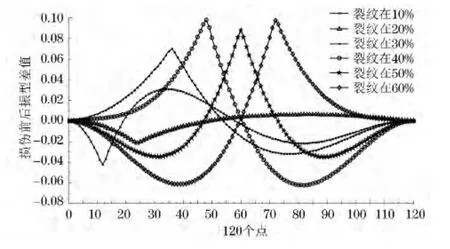
图3 损伤振型差值变化曲线

含有裂纹的位置上的振型变化相对于周围位置会忽然增大或者减小，从而可以判断裂纹的确切位置，并可以具体到单元的点上。

2.2 BP神经网络法对简支梁位置深度识别

计算程序中，神经网络的隐含层选择S型传递函数tansig，输出层选择线性传递函数purelin，而训练函数则选择trainlm。通过不断地训练测试，观察神经元数目和学习速率对网络训练的影响。最终选择神经元数目为4，学习速率为0.05，在训练进行到666步时，就已经达到预期的误差效果。以第一阶模态振型改变率为例，如表3所示。

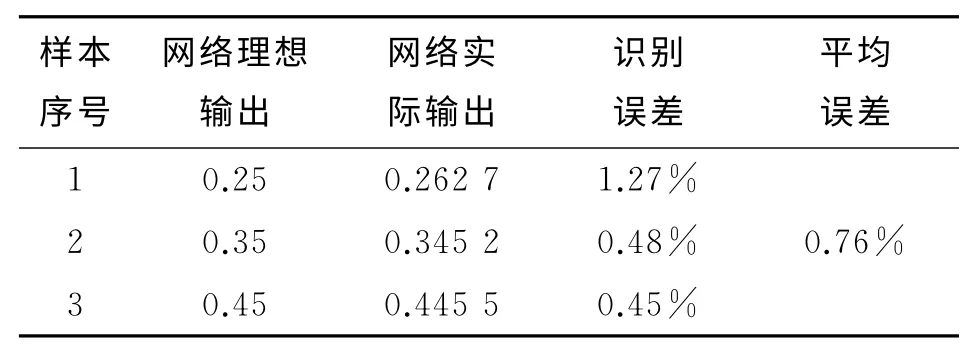
表3 基于第一阶模态振型改变率的损伤程度识别误差

从表3中可以看出，其识别误差对深度大一点的裂纹控制在0.5%之内，说明了该BP神经网络模型完全可以作为简支梁中裂纹深度的损伤识别的指标。

2.3 能量密度法对裂纹简支梁位置及深度的识别［6］

定义物体的动能密度为：

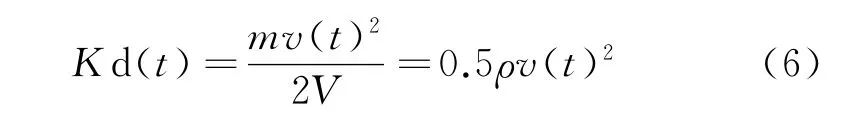
归一化处理，得到其相对值：

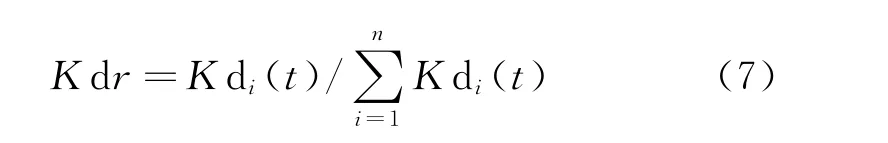
式中：Kdr为损伤指标；Kd（t）为每个时刻的动能密度；n为梁上的测点数。

通过动能密度损伤识别方法将裂纹位置为0.6L（L为裂纹长度）时，裂纹深度分别为20%、30%、40%时的损伤指标Kdr的变化描绘出来，如图4所示。

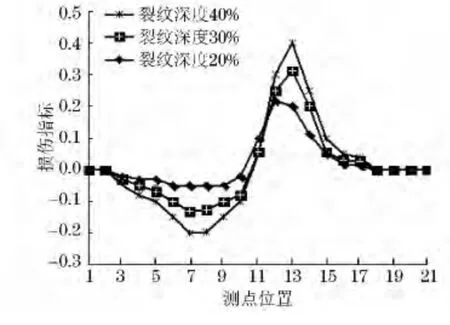
图4 损伤梁不同裂纹深度时损伤指标Kdr 的变化

裂纹深度不同时其损伤指标Kdr的变化曲线也不相同，且随着裂纹深度的增加，损伤指标Kdr不断增大。因此以损伤指标Kdr的正极值作为检测参数对裂纹梁的损伤程度进行定量判断。

2.4 试验模态分析

试验中的振动筛下横梁为长635 mm、宽10mm、高15mm 的梁，两端由螺丝固定到机架上，如图5所示。利用DASP（数据采集和信号处理）进行模态分析时，由于采用了高弹性聚能力锤和先进的变时基频响函数分析技术，用力锤敲击就能进行模态试验以及进行环境激励模态分析。

图5 振动筛横梁

利用试验模态分析方法，求得完好和损伤简支梁的振型和频率。确定简支梁的频率分布，进而确定简支梁的薄弱部位。现场测试传感器分布如图6所示，在该简支梁上人为制造裂纹。

图6 振动筛横梁

利用DASP中自带的模态分析模块对试验测得的数据进行模态分析，如图7所示。

试验主要分析2kHz内的固有频率，分析出简支梁前四阶的固有频率值以及简支梁前四阶固有频率的变化量和变化率，最后分析了不同损伤程度的简支梁固有频率试验与理论计算的误差。如表4所示，笔者中只列出60%裂纹深度的验证。

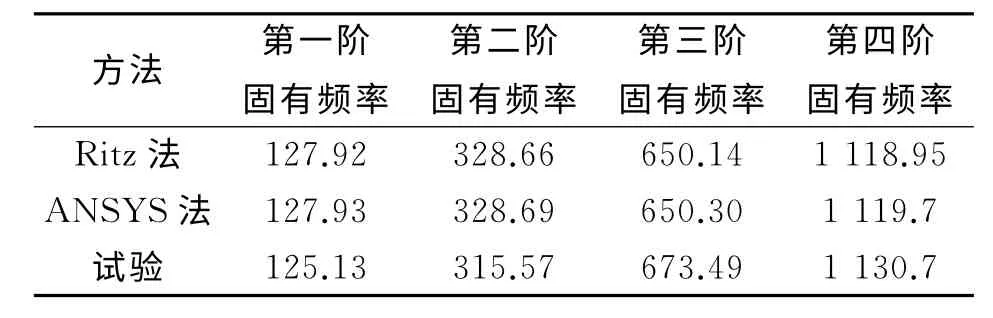
表4 60%裂纹深度的简支梁固有频率的试验与理论值比较 Hz

3 结论

（1）利用模态参数的变化来诊断结构的裂纹故障是可行的。

（2）裂纹的存在会引起局部刚度下降，使结构的各阶模态的固有频率均有下降。

（3）裂纹对模态参数的影响随着裂纹深度的增大而增大，固有频率这一参数易于准确测量。所以，根据结构固有频率下降的程度可以诊断结构裂纹故障的严重程度。

但是从表中的裂纹诊断结果来看，裂纹的诊断精度比理论计算和仿真诊断的精度都要低。其原因有：

（1）由于试验条件的限制，试验时单元节点比较少，测得的数据少，从而影响了诊断的精度。

（2）冲击力锤单次激励的模态试验方法，对于相对大型的梁结构来说响应模态是不完整的，即结构的固有特性不能够充分地激发出来。实际结构中总是存在着各种各样的阻尼，尤其对于复杂结构，其阻尼一般不容易确定，而在理论分析中，求得的是结构无阻尼情况下的模态参数。

（3）环境噪声也会影响测量的精度，试验时正好在工人切割板块的现场，所以环境噪声很大，而理论分析中，求得的是无噪声条件下的模态参数。

［1］ 郑渝.机械结构损伤检测方法研究［D］.太原：太原理工大学，2004.

［2］ 李建忠，刘国奇，陈振华，等.基于小波包分解的不锈钢焊缝超声TOFD 检测信号及缺陷信号提取［J］.无损检测，2015，37（1）：38－41.

［3］ 刘贵杰，徐萌，李思乐，等.基于小波能量系数的海洋平台管节点疲劳裂纹扩展AE 信号识别［J］.无损检测，2013，35（2）：1－7.

［4］ DOUKA，TROCHIDIS.Crack identification in plates using wavelet analysis［J］.Journal of Sound and Vibration，2004，270（2）：279－295.

［5］ 苏金明，张莲花，刘波，等.实MATLAB 工具箱应用［M］.北京：电子工业出版社，2004.

［6］ 陈晓强，朱宏平，王丹生，等.基于动能密度和弯曲弹簧模型的裂纹梁损伤识别［J］.华中科技大学学报，2008，25（1）：52－54.