循环加载下塑性混凝土的应力-应变曲线分析
2015-12-04刘璐璐常芳芳王雪奎
刘璐璐,常芳芳,解 伟,王雪奎
(1.华北水利水电大学 土木与交通学院,郑州 450011;2.黄河水利委员会 黄河水利科学研究院,郑州 450003)
1 研究进展
普通混凝土具有抗压强度高、耐久性能好等诸多优点,被广泛应用于建筑领域[1],但是普通混凝土的应力-应变曲线特征与土的应力-应变曲线特征相差比较大,造成了普通混凝土使用的局限性。
在大坝围堰、除险加固及结构基础工程中,防渗体与周围的土体紧密接触,为了避免墙体内出现拉应力,并且为了使混凝土与周围土体的变形相近,减小结构的破坏程度,延长结构的使用时间,就需要一种低强度、低弹性模量、大应变和防渗性好的材料。经过长时间的研究,人们发现用膨润土或黏土代替普通混凝土中的部分水泥可以满足这样的要求,即塑性混凝土。通过应力-应变曲线不仅可以得到混凝土的抗压强度,还可以确定其弹性模量、峰值应变、延性指数、破坏形态等力学特性[1]。
我国对塑性混凝土的研究始于20世纪80年代[2],但大多侧重于工程实际应用,缺乏较系统的理论研究,以往的塑性混凝土应力-应变曲线研究[3-5]主要针对的是未预压时的应力-应变曲线,而对循环加载下的应力-应变曲线的研究并不是太多,譬如王四巍等人[6]研究了循环加载下塑性混凝土的强度及变形特性。
2 试验方案
2.1 试验原材料及塑性混凝土配合比
(1)水泥,采用河南孟电生产的P·O 32.5号普通硅酸盐水泥,各项指标符合《通用硅酸水泥》(GB175—2007)标准要求。
(2)细骨料为河砂,级配曲线位于Ⅱ区,属于中砂,各项指标符合《建筑用砂》(GB/T14684—2001)标准要求。
(3)粗骨料粒径5~25 mm的石灰岩碎石,级配连续,各项指标符合《建筑用卵石、碎石》(GB/T14685—2001)标准要求。
(4)水为自来水。
(5)膨润土选用四川乐山生产的钠质膨润土。
混凝土配合比见表1。

表1 塑性混凝土配合比Table 1 Mix proportions of plastic concretes
2.2 试件的制作
主要开展圆柱体和棱柱体单轴抗压力学特性指标试验,其中棱柱体试件尺寸为150 mm×150 mm×300 mm,圆柱体试件尺寸为Ф150 mm×300 mm,每组配合比均浇筑6个棱柱体试件和6个圆柱体试件。每组试件中3个圆柱体和3个棱柱体试件做轴心抗压强度试验,另外3个圆柱体和3个棱柱体试件做弹性模量试验。
事先准备好材料,试验开始时按照表1中的配合比称取每种材料的量,拌合方式采用强制式搅拌机拌合,在往搅拌机里倒料之前先用水预湿,然后依次加入粗细骨料、水泥、膨润土开始搅拌,搅拌的过程中加水,2 min之后出料,同时在搅拌的过程中另外的试验人员对试模刷脱模剂。试件成型静置48 h后拆模,并移至标准养护室养护,养护至28 d龄期后按照《水工混凝土试验规程》[7]进行抗压强度和弹性模量试验。
2.3 试验设备与过程
试验采用全标距法开展,采用微机控制的CMT5105电子万能试验机,力的加载用位移进行控制,做轴心抗压强度试验时加载速度为1 mm/min,做弹性模量试验时加载速度为0.2 mm/min。
由于膨润土的加入,拌合出的塑性混凝土较粘,这难免会给试件的浇筑带来影响,尽管在浇筑的时候对混凝土进行了振捣,但混凝土之间仍存留些气泡。为了消除试件内部的孔隙,试验采用预压和不预压2种方案,预压的最大值为0.4倍的峰值荷载,预压段共循环2次。轴向荷载、试件的变形位移均由仪器自动采集,然后计算机根据采集到的数据自动绘制应力-应变曲线。
3 试验结果分析
3.1 基本的试验结果
每组配合比下试件结果的处理方法:以3个试件测定值的算术平均值作为该组试件的抗压强度值。当3个测定值中的最大或最小值有一个与中间值的差值超出中间值的15%时,则把最大及最小值一并舍去,取中间值作为该组试件的试验值[2]。
对于弹性模量的计算,现有规范及研究成果尚无统一规定取值方法[2],大多数的研究主要是根据《水工混凝土试验规程》[7]中的公式来计算的。式中:E为试件的弹性模量(MPa);p2为峰值应力的40%(N);p1取应力为0.5 MPa时的荷载值(N);A为试件的承压面积(mm2);ΔL为试件从p1增加到p2时的纵向累计变形值(mm);L为试件的变形测量标距(mm)。
由于本试验混凝土的强度不高,若采用上述的公式来计算弹性模量,p1和p2的取值间的距离太近甚至会出现负值,这样计算出来的弹性模量没有代表性也不符合实际,那么就需要一种新的取值方法来计算弹性模量。
初始弹性模量的取值应为原点处的切线斜率,但塑性混凝土的应力-应变曲线与普通混凝土的应力-应变曲线不同,它有一个初始加载段,原点处的斜率接近于0,则用原点处的斜率来计算初始弹性模量不太合适。
本试验试件的弹性模量和初始弹性模量按照宋力等[2]提出的方法计算:p2为极限破坏荷载的90%;p1为试件的初始荷载,根据其切线斜率的变化,取极限破坏荷载的40%;初始弹性模量E初主要针对未预压构件,其中p2为极限破坏荷载的4.7%,对应的应变约为峰值应变的15%,p1为极限破坏荷载的2.5%。试件的基本试验结果见表2。
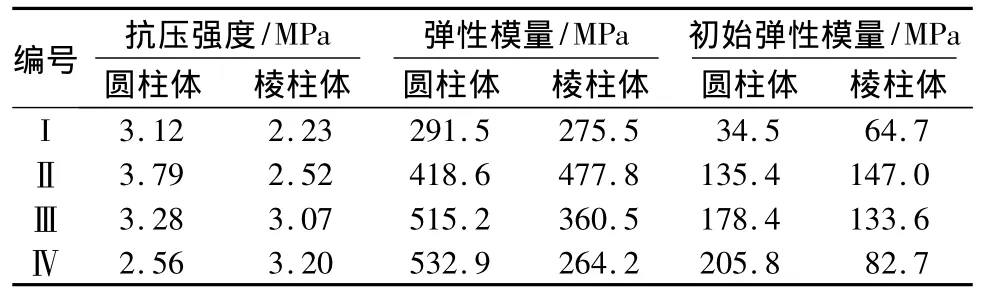
表2 试件的基本试验结果Table 2 Basic test results of specimens
3.2 循环加载下的应力-应变曲线
图1为塑性混凝土循环加载下的应力-应变曲线。试验表明,塑性混凝土的循环加载下的应力-应变曲线的形态与单调加载下的应力-应变曲线形态基本一致。再者与普通混凝土相比,从曲线的走势看塑性混凝土的应力-应变曲线出现了初始加载段、反弯点和拐点,从曲线的数值上看塑性混凝土的峰值应力减小,峰值应变增大,上升段斜率减小,进而导致塑性混凝土的弹性模量比普通混凝土有所减小。造成这种现象主要是因为混凝土中部分的水泥被膨润土代替,致使塑性混凝土既要表现水泥影响强度的特性同时也要表现膨润土影响变形的特性,这样塑性混凝土的强度就会因水泥量的减少而降低,变形因膨润土的加入而明显变大,进而导致弹性模量的减小。
塑性混凝土应力-应变曲线基本上可以分5个阶段(见图2):OA,AB,BC,CD 和循环段 O'a。OA,AB,BC,CD 段曲线的特征,宋力等[2]已作了详细的描述。曲线在达到峰值应力之前试件表面无肉眼可见裂缝,试件变形以体积压缩和微裂缝发展为主[6]。刚开始加载,由于试件内部缺陷和孔隙的存在,曲线出现初始加载段和反弯点A;进入到循环段O'a阶段,由于循环荷载的存在,反弯点变得不是很明显;OA,AB和BC 3个阶段试件主要以轴向的变形为主,试件表面都未出现裂缝,但是随着轴力的继续增加,过了C点轴向变形达到了一定程度,试件表面开始出现微小裂缝,起初的裂缝出现在试件中间部位,而后沿斜向上、下端发展,待轴力、轴向变形达到D点时试件表面的裂缝发展较快,一直贯穿整个截面形成主斜裂缝,主斜裂缝不断加宽直至试件破坏,试件破坏过程见图3。

图1 塑性混凝土循环加载下的应力-应变曲线Fig.1 Stress-strain curves of plastic concrete under cyclic loading

图2 典型的应力-应变曲线Fig.2 Typical stress-strain curve

图3 试件的破坏过程Fig.3 Process of specimen’s failure

图4 未预压段塑性混凝土的应力-应变曲线Fig.4 Stress-strain curves of plastic concrete in the absence of preloading
3.2.1 未预压的应力-应变曲线
图4中无论是棱柱体还是圆柱体,在做弹性模量的试验中预压和未预压后的应力-应变曲线在上升段出现了差异。差异主要体现在峰值应力的0.4倍处,即预压荷载的最大值处(图2点a处),这里定义为奇异点,该点所对应的应变为峰值应变的20%~30%。图5为其中1条曲线奇异点前预压和未预压段的应力-应变曲线段,图6为2条曲线段的斜率。由图5和图6可以看出,未预压的试件在做弹性模量试验时刚开始段应变的变化速度比应力的变化速度快,这证明了之前所说的孔隙的存在。同时,预压段与未预压段有一明显的不同,预压段的应力-应变曲线的斜率先增加后减小,而未预压段的曲线斜率一直增加。通过分析我们更加了解试件内部孔隙的存在的微观性。
奇异点出现的主要原因就是所设置的最大预压应力比较小,还未能完全消除试件内部的孔隙。本次试验预压应力的最大值是根据《水工混凝土试验规程》(SL352—2006)[6]取得的,根据试验结果及分析可知普通混凝土的试验规程不完全适用于塑性混凝土。
3.2.2 循环段的应力-应变曲线
由图2可知,塑性混凝土在循环荷载作用下的加载曲线与卸载曲线不重合,加载曲线和卸载曲线形成闭合曲线,即塑性混凝土加卸载的路径不能完全重合,应力与应变之间不存在一一对应关系[6]。经过对试验数据分析,我们做出循环段曲线的斜率见图7,可以看出这2次循环曲线的斜率在走势上和数值上基本一致,这就说明了在做弹性模量试验的时候预压次数对应力-应变曲线的影响并不大。

图5 奇异点前典型的应力-应变曲线Fig.5 Typical stress-strain curves before the singular point occurs
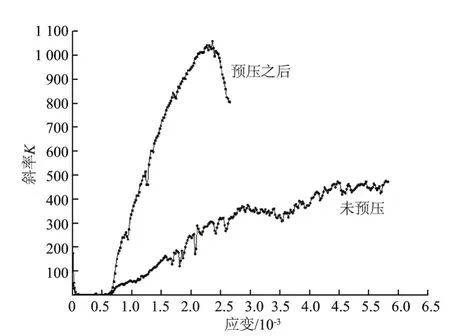
图6 奇异点前的应力-应变曲线段的斜率Fig.6 Slope of the stress-strain curves before the singular point occurs
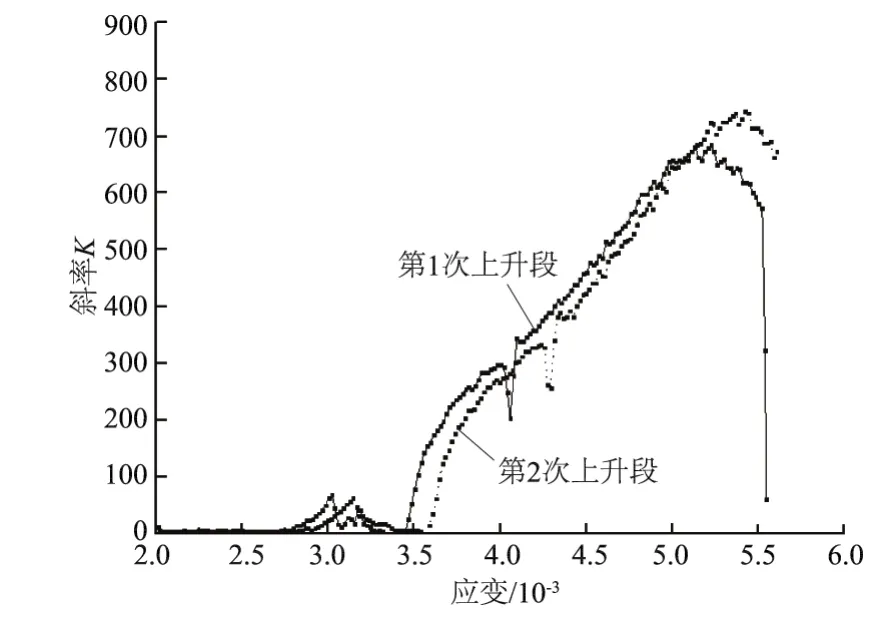
图7 循环段应力-应变曲线斜率Fig.7 Slope of the stress-strain curve of cycle segment
4 结论
本文通过试验研究塑性混凝土在加卸载作用下应力-应变曲线的特点,分析了预压与未预压以及循环段的应力-应变曲线的特征,得出以下结论:
(1)曲线的上升段较普通混凝土有明显的不同,从曲线的走势看塑性混凝土出现了初始加载段和反弯点,从曲线的数值上看峰值应力减小,峰值应变增大,上升段斜率减小,进而导致塑性混凝土的弹性模量比普通混凝土有所减小。
(2)预压段的应力-应变曲线的斜率先增加后减小,而未预压段的曲线斜率一直增加。通过分析试件内部内部孔隙存在的微观性。
(3)循环曲线的斜率在走势上和数值上基本一致,预压次数的多少对应力-应变曲线的影响并不大。
[1]于 良,程 华,靳雨欣,等.碳纤维混凝土单轴受压应力-应变本构关系[J].后勤工程学院学报,2013,(4):6-12.(YU Liang,CHENG Hua,JIN Yu-xin,et al.Constitutive Relationship of Stress-strain of Carbon Fiber Reinforced Concrete under Uniaxial Compression[J].Journal of Logistical Engineering University,2013,(4):6-12.(in Chinese))
[2]宋 力,常芳芳.塑性混凝土应力-应变特性的试验研究[J].南水北调与水利科技,2014,12(2):67-70.(SONG Li,CHANG Fang-fang.Study on Stress-strain Characteristics of Plastic Concrete[J].South to North Water Diversion and Water Science& Technology,2014,12(2):67-70.(in Chinese))
[3]高丹盈,王四巍,宋帅奇,等.塑性混凝土单向受压应力-应变关系的试验研究[J].水利学报,2009,40(1):82-87.(GAO Dan-ying,WANG Si-wei,SONG Shuai-qi,et al.Experimental Study on the Stress-strain Relationship of Plastic Concrete under Uniaxial Compression[J].Journal of Hydraulic Engineering,2009,40(1):82-87.(in Chinese))
[4]胡良明.塑性混凝土受压本构关系模型与破坏准则[D].郑州:郑州大学材料科学与工程学院,2012.(HU Liang-ming.Constitutive Model and Failure Criteria of Plastic Concrete under Compression[D].Zhengzhou:School of Materials Science and Engineering of Zhengzhou University,2012.(in Chinese))
[5]PASHANG PISHEH Y,MIR MOHAMMAD HOSSEINI S M.Stress-strain Behavior of Plastic Concrete Using Monotonic Triaxial Compression Tests[J].Journal of Central South University of Technology,2012,19(4):1125-1131.
[6]王四巍,高丹盈,刘汉东.循环加卸载下塑性混凝土强度及变形特性[J].工业建筑,2009,39(5):92-95.(WANG Si-wei,GAO Dan-ying,LIU Han-dong.Study on Strength and Deformation of Plastic Concrete under Cyclic Loading and Unloading[J].Industrial Construction,2009,39(5):92-95.(in Chinese))
[7]SL352—2006,水工混凝土试验规程[S].北京:中国水利水电出版社,2006.(SL352—2006,Test Code for Hydraulic Concrete[S].Beijing:China Water Power Press,2006.(in Chinese))
