混凝土中锚杆锚固强度的SVM回归模型

雷进生，陈建飞，2，王乾峰，彭 刚，曾有为

(1.三峡大学土木与建筑学院，湖北宜昌 443002;2.福州大学阳光学院，福州 350000)

1 研究背景

锚杆作为岩土工程的支护结构已得到广泛应用，钢锚杆具有成本低廉、施工简便、支护及时及能充分调动围岩自承能力的技术特点［1］。许多学者也对锚杆对围岩的锚固作用方面进行了大量研究，并且形成了一定的理论体系［2－4］。同时，混凝土中锚杆锚固技术的应用领域也日渐广泛，在井巷与隧洞支护加固、建筑扩建改造、设备安装、结构抗震加固、建筑幕墙施工项目中，混凝土中锚杆锚固技术以其高效、灵活、经济等优势倍受青睐［5］。混凝土中的锚杆，与普通锚杆的原理是相通的［6］。但由于早龄期混凝土结构是一个混凝土强度和结构外形不断随时间变化的“时变结构”，混凝土与锚杆相互作用时锚杆的工作性状，是工程中非常关心的问题。但由于锚杆与混凝土相互作用的复杂性，所涉及的工程条件及混凝土特性参数通常是不确定的、模糊的，各影响要素之间可能存在复杂的非线性关系，往往使得锚固效应采用传统的方法和确定的数学模型进行描述存在困难和不足。近年来随着计算机技术的进步，机器学习方法逐步广泛应用于工程领域，为混凝土中锚杆锚固强度的回归预测和锚杆荷载传递机理研究等提供了有力支持。

支持向量机(SVM)是一种新的机器学习方法［7］，具有小样本、非线性以及高维模式识别的特点。基于Vapnik创建的统计学理论，采用结构风险最小化准则，在最小化样本误差点的同时，最小化结构风险，提供了模型的泛化能力，且没有数据维数限制，能适度抑制过拟合，被认为优于人工神经网络，并已成功地应用于模式识别(聚类)、函数逼近和预测等方面［8－13］。支持向量机方法建模不必知道因变量和自变量之间的关系，通过对样本的学习即可获得因变量和自变量之间非常复杂的映射关系。早龄期混凝土中锚杆的锚固强度预测可以看作是锚固强度与其对应影响因素之间复杂的非线性函数关系的逼近问题，本文尝试利用SVM回归算法对早龄期混凝土中锚杆的锚固强度建立数学模型，并根据此模型对锚固强度进行预测。

2 SVM预测模型

Vapnik等人对有限样本的机器学习进行了深入研究，提出了结构风险最小化(structural risk minimization，SRM)原则，在最小化样本点误差的同时可以最小化结构风险，并在此基础上建立了通用的支持向量机算法，后又引入不敏感损失函数ε，得到回归型支持向量机［14－17］。其基本思想是从样本数据中寻找一个最优分类面，即对给定的数据逼近的精度与逼近函数的复杂性之间寻求折衷，以期获得最好的泛化能力，如图1所示，图中ξ为松弛变量。

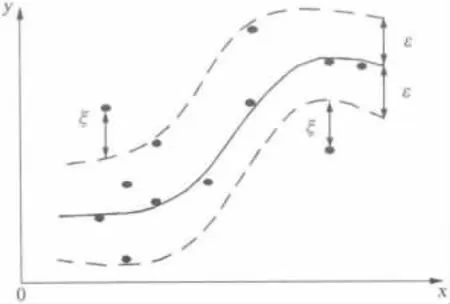
图1 非线性不敏感带示意图Fig.1 Diagram of nonlinear insensitivity zone

支持向量机回归预测时用惩罚因子C来判断回归函数误差的大小，C越大表示对训练误差大于ε的样本惩罚越大，ε规定了回归函数的误差要求，ε越小表示回归函数的误差越小。定义ε为线性不敏感损失函数。

式中:f(x)为回归函数返回预测值;y为对应的真实值。

具体算法如下。

(1)设训练样本 T={(xi，yi)，i=1，2，…l}，xi(xi∈Rd)是第i个训练样本的输入列向量，xi=，为对应的输出量。这里，d为样本个数，l为训练样本个数，R为实数。选择合适的正数 ε和 C，选择适当的核函数 K(xi，xj)=ø(xi)，ø(xj)，构造并求解最优化问题。

(2)求解式(2)得到最优解 α=［α1，α2，…，，构造决策回归函数为

式中:

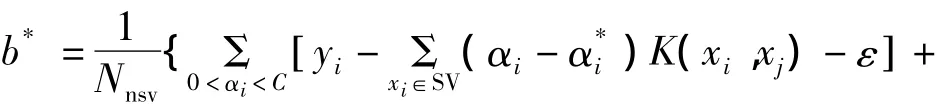
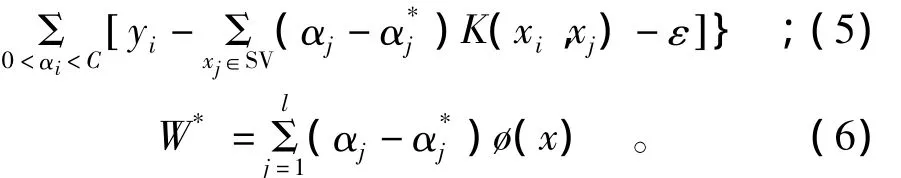
式中:Nnsv为支持向量个数;ø(x)为非线性映射函数;w，b，α和α*为建立SVM模型待确定的系数。

(3)利用回归函数对测试集进行预测。记录测试集的均方差E和决定系数R2，具体计算公式分别为:

式中:l为测试集样本个数;yi(i=1，2，…，l)为第 i个样本的真实值;^yi(i=1，2，…，l)为第i个样本预测值。

(4)根据E和R2对已建立的回归模型进行评价。如果性能未达到要求，则通过改变核函数以及其他模型参数等方法重新建模，直至性能满足要求。

3 基于SVM的锚固强度预测

3.1 混凝土中锚杆锚固强度试验

结合混凝土早龄期物理力学特性，对不同直径和不同锚固长度的锚杆在混凝土不同龄期进行拉拔试验。C25混凝土配合比为水∶水泥∶砂∶碎石=0.5∶1∶1.65∶3.34。Φ18 mm、Φ20 mm 和 Φ22 mm 3种不同直径锚杆预埋到试件中(锚固长度为300 mm、150 mm)。待试件成型后，分别于1，2，3，7 及28 d 龄期时进行拉拔试验，试件均产生混凝土劈裂破坏，混凝土与锚杆分离明显。试验结果见表1、表2。

锚固体向混凝土传递荷载，传递的机理比较复杂。为了更好地评价锚固长度、钢筋直径及龄期对钢筋在混凝土中的锚固强度的影响，考虑到小样本多因素的原因使得锚固强度试验值离散性较大，故采用支持向量回归思想，在试验数据中随机选取20组为训练样本，见表1;其余10组为预测样本，见表2，运用Matlab语言编写程序，建立支持向量机回归模型。

3.2 产生训练集和测试集

T={(xi，yi)，i=1，2，…，l}，其中 xi(xi∈Rd)是第i个训练样本的影响因素，包括锚固长度、锚固直径和龄期，yi∈R为对应的锚固强度试验值。

3.3 创建回归模型

混凝土中锚杆锚固强度的分析计算中，通过比较发现径向基核函数(RBF)［18－19］K(xi，x)=exp(－‖xi－x‖/σ2)的计算精度最高，故本研究根据RBF核函数，利用交叉验证方法寻找最佳的参数C和核函数中方差g，并设定不敏感系数ε=10－5，根据公式(3)实现SVM回归模型的创建和训练。

表1 训练样本数据Table 1 Training sample data

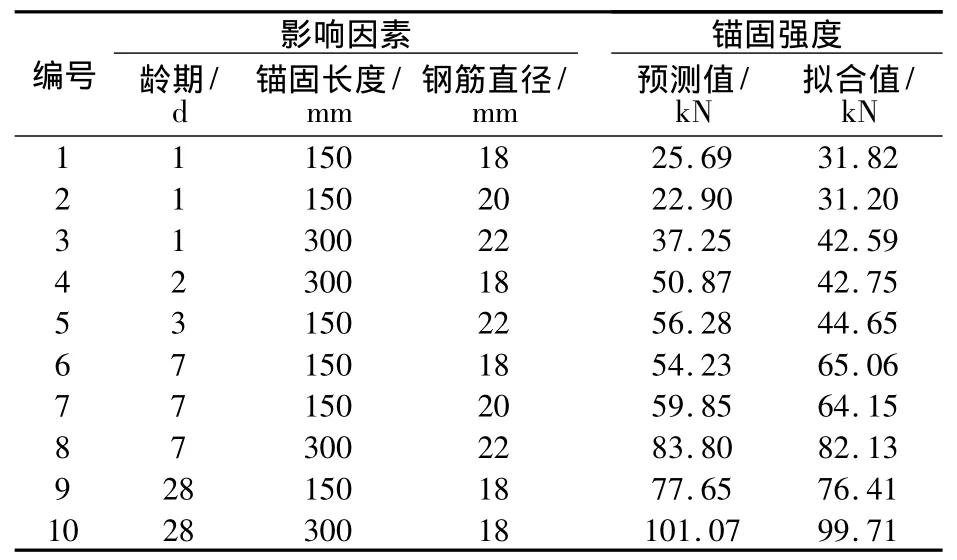
表2 预测样本数据Table 2 Predicted sample data

3.4 仿真预测

经交叉计算选取最佳参数 C=337.794 0和g=0.041 2，训练集和测试集预测结果如图2。

SVM训练集中计算所得 E=0.013 9，R2=0.948，测试集计算所得 E=0.023，R2=0.919，预测结果与真实值十分接近。对比图2(b)中BP神经网络 预测所得，有E=0.139，R2=0.525，其预测结果与真实值相差较大。说明在采用相同训练集前提下，SVM预测结果稳定性高于BP神经网络，对于混凝土这种离散性较小的材料来说支持向量机更适用;对较小样本进行预测，其性能明显优于BP神经网络。图3是经SVM回归预测后的龄期－锚固力关系曲线。

图2 训练集和测试集预测结果对比Fig.2 Comparison of training set results and test set results

图3 回归预测后龄期－锚固力关系曲线Fig.3 Curves of age vs.anchoring force after regression prediction

4 结论

锚杆在混凝土中兼具受力钢筋的特性，依靠单纯的理论分析建立锚固强度预测模型较困难;通过室内试验获得数据量十分有限，使得BP神经网络预测结果精度较低。引入人工智能领域中的支持向量机算法，对早龄期混凝土中锚杆锚固强度进行拟合和预测，建立了以混凝土龄期、锚固长度、锚杆直径多因素影响下的混凝土中锚杆锚固强度预测的SVM模型。

将此模型预测结果与试验值和BP网络计算结果进行对比。研究表明:SVM方法相对BP神经网络预测具有较高的精度，能够较好地模拟混凝土中锚杆锚固强度随各种因素的变化趋势，尤其是锚固强度随龄期的发展趋势;建立的SVM模型学习效率高对新鲜样本的适应能力较强，预测结果与试验结果吻合较好，受样本数量影响较小。运用SVM理论可以对混凝土中锚杆锚固强度的控制提供依据，也为锚固强度的预测提供了一个科学有效的方法。

SVM模型是根据较少的样本训练得出的，但是随着试验数据的不断增加，可以继续进行学习，得到更完善的预测体系，使预测值更接近真实值，从而进一步提高预测精度，并应用于实际工程。支持向量机方法可不断根据新的数据资料对效应变量进行滚动预测，这种预测具有实时性和较高的精度。该方法可用于岩土力学、结构力学与工程中的各个方面，可为工程的设计和施工提供很好的途径。

［1］汤 雷，陆士良，高加胜.锚杆拉拔试验的意义［J］.矿山压力与顶板管理，1996，(2):68－70.(TANG Lei，LU Shi-liang，GAO Jia-sheng.Significance of Bolt Pullout Test［J］.Ground Pressure and Strata Control，1996，(2):68－70.(in Chinese))

［2］杨双锁，张百胜.锚杆对岩土体作用的力学本质［J］.岩土力学，2003，24(增):279－ 282.(YANG Shuang-suo，ZHANG Bai-sheng.The Influence of Bolt Action Force to the Mechanical Property of Rocks［J］.Rock and Soil Mechanics，2003，24(Sup.):279－282.(in Chinese))

［3］康红普，姜铁明，高富强.预应力在锚杆支护参数的设计［J］.煤炭学报，2008，33(7):721－726.(KANG Hong-pu，JIANG Tie-ming，GAO Fu-qiang.Design for Pretensioned Rock Bolting Parameters［J］.Journal of China Coal Society，2008，33(7):721－726.(in Chinese))

［4］舒谷生，彭文祥，何忠明.全长粘结式锚杆拉拔试验的数值实现［J］.科技导报，2009，27(12):47－50.(SHU Gu-sheng，PENGWen-xiang，HE Zhong-ming.Numerical Simulation of the Pullout Test of Wholly Grouted Cable［J］.Science and Technology Review，2009，27(12):47－50.(in Chinese))

［5］谷拴成，崔希鹏.混凝土中锚杆锚固荷载传递特性研究［J］.混凝土，2010，(10):27－30.(GU Shuan-cheng，CUI Xi-peng.Characteristic Research on the Anchorage Load Transfer of Bolt in Concrete［J］.Concrete，2010，(10):27－30.(in Chinese))

［6］徐 波，吴智敏.混凝土中锚杆荷载传递机理的理论分析［J］.哈尔滨工业大学学报，2006，38(3):417－419.(XU Bo，WU Zhi-min.Analysis of Load-transfer Mechanism of Anchors in Concrete［J］.Journal of Harbin Institute of Technology.2006，38(3):417－ 419.(in Chinese))

［7］VAPNIK V N.The Nature of Statistical Learning Theory，(Second Edition)［M］. New York:Spring-Verlag，1999.

［8］陈 斌，郭雪莽，刘国华.基于粗糙集(RS)和支持向量机(SVM)的混凝土性能预测实证研究［J］.水力发电学报，2011，30(6):251－ 257.(CHEN Bin，GUO Xue-mang，LIU Guo-hua.Prediction of Concrete Properties Based on Rough Sets and Support Vector Machine Method［J］.Journal of Hydroelectric Engineering，2011，30(6):251－ 257.(in Chinese))

［9］武换娥，丁圣果，巩玉志，等.支持向量回归机在混凝土强度预测中的应用研究［J］.工业建筑，2007，37(增1):991－995.(WU Huan-e，DING Sheng-guo，GONG Yu-zhi，et al.Research on Support Vector Machine’s Prediction of Concrete Strength［J］.Industrial Construction，2007，37(Sup.1):991－995.(in Chinese))

［10］崔海霞.高强混凝土强度预测的支持向量机模型及应用［J］.混凝土，2010，(5):49－ 51.(CUI Hai-xia.Strength Prediction of High Strength Concrete Using SVM and Its Application［J］.Concrete，2010，(5):49－ 51.(in Chinese))

［11］朱怡翔，石广仁.火山岩岩性的支持向量机识别［J］.石油学报，2013，34(2):312－ 322.(ZHU Yi-xiang，SHI Guang-ren.Identification of Lithological Characteristics of Volcanic Rocks by Support Vector Machine［J］.Acta Petrolei Sinica，2013，34(2):312－322.(in Chinese))

［12］冯夏庭，赵洪波.岩爆预测的支持向量机［J］.东北大学学报(自然科学版)，2002，23(1):57－59.(FENG Xia-ting，ZHAO Hong-bo.Prediction of Rockburst Using Support Vector Machine［J］.Journal of Northeastern University(Natural Science)，2002，23(1):57－59.(in Chinese))

［13］赵洪波，冯夏庭.非线性位移时间序列预测的进化-支持向量机方法及应用［J］.岩土工程学报，2003，25(4):468－ 471.(ZHAO Hong-bo，FENG Xia-ting.Study and Application of Genetic Support Vector Machine for Nonlinear Displacement Time Series Forecasting［J］.Chinese Journal of Geotechnical Engineering， 2003，25(4):468－471.(in Chinese))

［14］VAPNIK V，LERNER A.Pattern Recognition Using Generalized Portrait Method［J］.Automation and Remote Control，1963，(24):774－780.

［15］VAPNIK V.Estimation of Dependence Based on Empirical Data［M］.New York:Springer-Verlag，1982.

［16］CORTESC，VAPNIK V.Support Vector Networks［J］.Machine Learning，1995，(20):1－25.

［17］陈永义，余小鼎，高学浩.处理非线性分类和回归问题的一种新方法(Ⅰ)——支持向量机方法简介［J］.应用气象学报，2004，15(3):345－354.(CHEN Yong-yi，YU Xiao-ding，GAO Xue-hao.A New Method for Nonlinear Classify and Non-linear RegressionⅠ:Introduction to Support Vector Machine［J］.Quarterly Journal of Applied Meteorology，2004，15(3):345－354.(in Chinese))

［18］燕孝飞，葛洪伟，颜七笙.RBF核SVM及其应用研究［J］.计算机工程与设计，2006，27(11):1996－2011.(YAN Xiao-fei，GE Hong-wei，YAN Qi-sheng.SVM with RBF Kernel and Its Application Research［J］.Computer Engineering and Design，2006，27(11):1996－ 2011.(in Chinese))

［19］邓乃扬，田英杰.数据挖掘中的新方法－支持向量机［M］.北京:科学出版社，2005.(DENG Nai-yang，TIAN Ying-jie.New Method of Data Mining:Support Vector Machine［M］.Beijing:Science Press，2005.(in Chinese ))