货币洪流中演化的中国股价波动复杂度耦合关系——基于2000至2014年数据的经验证据

温博慧

(天津财经大学经济学院，天津 300222)

一、引 言

股价作为重要资产价格变量在经济金融体系中扮演着不可忽视的角色［1］［2］，量化认识股价波动特征及其可控性至关重要。然而，股票市场中存在时间不可逆，线路多重因果反馈以及不确定性，使股价波动具有了传统金融理论所窘于解释的复杂非线性动力系统特征。复杂度，即对复杂性程度的测算，已被学术界广泛认可为最适合用于分析非线性系统的动力学特征参数和市场效率评价指标［3］。虽然技术上的固有约束和符号转换方式上的缺陷均是股价波动复杂度测算方法的有待改进之处，但何为股价波动复杂度的影响因素?其来自于市场内部还是外部?如果外部冲击力可以改变整个市场数据结构特征，那么这一关键的外部影响因素又是什么?上述系列问题构成学界进一步思索的诉求。

与此同时，反观股票市场的外部环境，国际市场货币环境变化与股价波动趋势转变相伴相生［4］，中国股票市值总额占GDP比重持续增长和经济货币化程度奇高迷题并存［5］的事实，使得货币化程度开始被质疑是否蕴含与股价波动特征及其可控性的关系。尽管股价波动属市场行为，但中国股市6100点时的高货币存量和在2014年11月21日央行宣布降息后股市启动的事实，显示了货币变化对股价波动的影响;股票市场整体波动最终取决于流动性攻击水平和企业盈利预期。由于货币化程度由货币供给和经济增长共同决定，因此，从相互协调和共同发展的耦合关系角度测定货币化程度与股价波动复杂度之间的动态关系，一方面可把握股价波动特征与变化趋势，另一方面可反映金融深化过程中市场效率的改变。中国股价波动复杂度随经济货币化程度变迁产生了怎样的历史演变规律?这种演化在时序程度等方面的量化关系又是什么?这些成为具有新生研究价值的问题。

针对上述问题，本文着重梳理并意欲从如下三方面做出拓展性创新:第一，为了使研究既能充分涵盖股指波动过程中的高频信息，又能与货币化程度数据的时间频度相匹配，笔者突破低频数据范围内的研究，以高频数据为基础，并借助滑窗技术将其信息转化于月度复杂度;第二，在对主流复杂度测算方法形成改进的同时，构造系统指标对中国股价波动的复杂性程度进行综合性测算;第三，在筛选并剔除影响时间序列复杂度的内部结构性因素后，突破经典回归方法和单纯性因果关系分析的局限，构建货币化程度与股价波动复杂度的耦合关系模型，从协调性与发展度两方面深入探讨二者动态交互作用的演化结果。

二、相关文献回顾

有关货币化程度变迁与股价波动复杂度演化问题的国内外相关研究成果可归纳并划分为复杂度测算方法、复杂度成因以及货币供给对股价波动的影响和因果分析框架的突破三方面。

主流的股价波动复杂度测算方法包括分数维、算法复杂度和熵算法三类。鉴于早期分数维计算方法无法实现通过维数对系统复杂度进行解释［6］，Kantelhardt和Zschiegner(2002)提出了多重分形消除趋势波动分析法(简称MF-DFA法)，以多重分形度表征系统复杂度［7］，但其对序列长度的较高要求也使自身陷入了测算效率困境［8］，即当时间序列长度较短时，小样本效应(finite-size effect)会导致虚假多重分形［9］。因此，如何应对小样本效应成为其新兴探寻方向［10］［11］。算法复杂度(又称kolmogorov复杂度)本身虽有着严格的数学理论依据，但需将给定时间序列转换成符号序列。近似熵(ApEn)和样本熵(SampEn)算法虽不涉及对时间序列的符号化转换，但对参数依赖性较高［12］。针对这一问题，Chen(2011)提出了模糊熵(FuzzyEn)算法。研究发现，模糊熵算法对序列长度的变化具有较好的一致性［13］，且对参数选择的敏感性和依赖性有所降低，测度结果的连续性更好。但遗憾的是，模糊熵算法仍未能摆脱对参数进行经验选择的需要［14］。上述成果表明，学术界对如何构建正确的股价波动复杂度测算模型尚未达成共识。在对样本效应进行修正的同时，将修正后的多重分形度计算法、基于兼容法的算法复杂度和模糊熵算法的测度结果构造成为复杂度测算综合指标，可以考虑成为兼容算法优势并对复杂性程度形成综合性测算和描绘的尝试。

在股价波动复杂度成因研究方面，序列的长程相关性和厚尾分布特征是研究者认为的复杂度的一般来源。Jozef等(2012)和周炜星(2010)指出，在重组和替代变换基础上序列的复杂性还可能源于小样本效应，但一些本身不具有复杂性特征的序列通过测度后也可能被实证为具有复杂性，即存在复杂性错觉［15］［16］。究其原因，一方面可能缘于测算方法不准确，另一方面可能忽视了形成序列波动复杂度的外部因素。

在直接研究货币化程度与股价波动复杂度关系成果并不多见的情况下，货币供应量对股价波动的影响可以形成一定的间接性回答。研究者认为，变化了的货币供应量可以通过影响投资者手持现金的比例来影响证券市场中的货币量，进而对股价波动带来正向影响。货币数量论也可对这种关系做出解释。国内学者围绕脉冲响应函数争论了我国不同层次货币供给变动对股价的影响效果，但鲜有对二者内在交互作用机制的论述。事实上，货币供给，乃至货币化程度能否对股价波动产生影响的问题不应单纯依长期或短期协整关系而判定，也不是变量间的因果关系分析即能完成的，而是要以系统论的思想综合而全面的分析变量间协同变动的耦合关系。

近年来，已有学者将耦合分析引入经济社会系统研究中，并展开初步应用［17］。耦合涵盖发展与协调两个方面。协调强调子系统之间相互配合和谐发展的紧密程度;而发展则体现系统由低级向高级的运动。因此，由协调与发展两者综合构成的系统的耦合关系，蕴含着协调的横向紧密联系和发展的纵向深入拓展两个不可或缺的组成部分。从本文的研究目标看，如果超越因果关系分析的约束，可以遐想在“货币化程度-股价波动复杂度”大系统中货币化程度与股价波动复杂度之间所存在的相互渗透、相互影响的耦合关系。对这一情况的判定需要借助综合测算方法与分析工具进行实证检验。

三、数据选取、阶段划分与时间序列内部结构性影响因素的剔除

(一)数据选取与阶段划分

本文将总样本区间设定为2000年2月至2014年6月。这一时期几乎横跨了中国改革开放以来股票市场和货币市场发展过程中所有相对重要的系列时段，并且数据相对完整，能提高实证分析的研究价值。

鉴于演化过程中阶段性存在的可能性和分阶段研究的必要性，笔者针对总样本区间进行阶段划分。就股票市场而言，2000年2月13日，中国人民银行和中国证监会联合发布《证券公司股票质押贷款管理办法》，允许符合条件的证券公司以自营的股票和证券投资基金作抵押向商业银行借款，是研究货币化对股价影响的重要时点;2005年4月29日，证监会正式发布了股权分置改革通知;从2005年5月到2007年9月，中国股票市场经历了高度繁荣的三年;从2007年10月到2009年3月，受美国次贷危机冲击，国内股指大幅下挫;从2009年4月至2014年6月股价波动进入后危机时代。就货币化程度而言，经季节调整后的中国货币化程度所体现出的四个阶段包括2000年2月到2007年9月的相对平稳阶段，2007年10月到2009年3月的加速上升阶段，2009年4月到2011年10月的高位平稳阶段，以及2011年11月至2014年6月的再次加速上升阶段(图1)。

综合我国股票市场和货币化程度发展的阶段性，并考虑避免因数据序列包含结构突变而导致的估计谬误，笔者将全样本数据区间最终划分为2000年2月至2005年4月，2005年5月至2007年9月，2007年10月至2009年3月，2009年4月至2011年10月和2011年11月至2014年6月五个阶段。

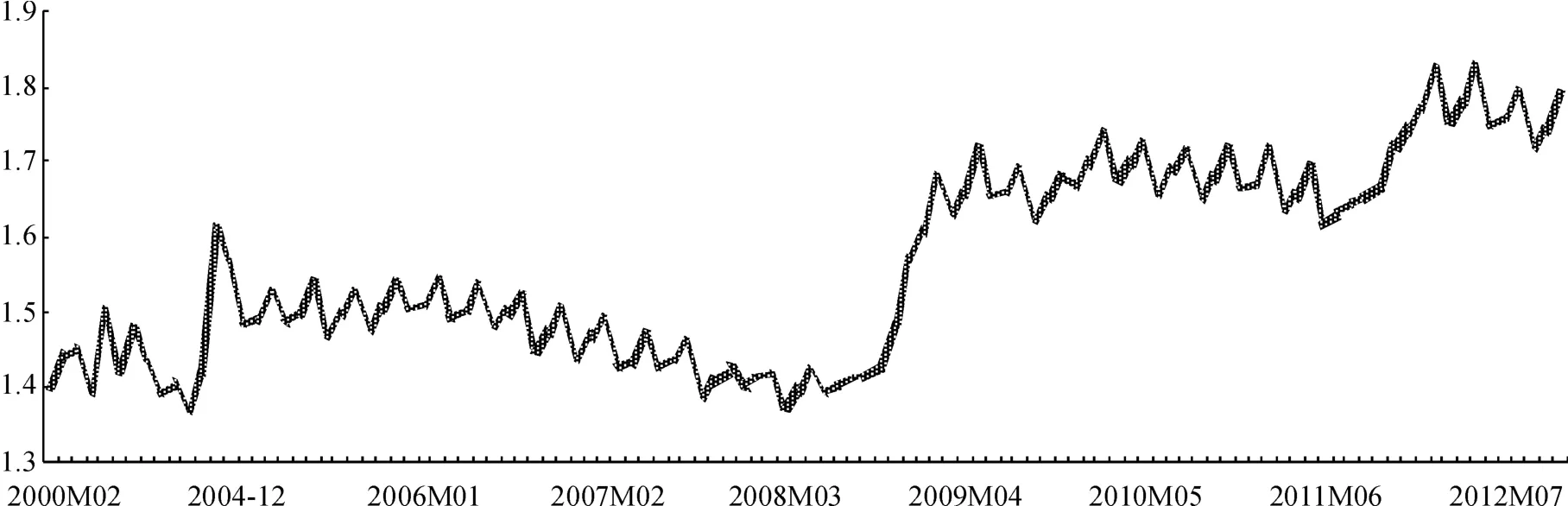
图1 中国货币化程度发展的阶段性变迁

在数据频率的选择方面:为避免收益率变量可能对非线性动力系统相依结构形成破坏，本文在实证分析中直接采用股票指数。同时，为了使研究既能充分涵盖股指波动过程中的高频信息，又能与货币化程度数据的时间频率相匹配，本文收集整理了深圳综合指数2000年2月14日至2014年6月30日的5分钟高频数据，并通过滑窗计算得到月度复杂度。选择深圳综合指数作为研究对象，主要是考虑到深圳股票市场中大盘股数量相对较少，资金推动效应容易表现得更为明显，从而可能鲜明反映股指复杂度与货币化程度变迁的关系。货币化程度数据选择经X-12季节调整后，月度M2存量÷(4×季度GDP)的计算值。其中，月度M2数据来源于中国人民银行网站，季度GDP数据来源于中经网统计数据库，深圳综合指数5分钟高频数据来源于锐思数据库。

(二)对影响股价波动复杂度的内部结构性因素的筛选和剔除

为了准确分析货币化程度变迁对股价波动复杂度演化的影响，需要筛选并剔除影响股价波动复杂度的时间序列内部结构因素。

由于重组变换可以打破序列的长期相依性，替代变换可以将非正态分布序列转变为正态分布。变换后序列多重分形度的减弱对应于原序列多重分形特征的来源。为此，笔者根据研究惯例，从MF-DFA分析法入手，筛选影响股价波动复杂度的序列内部结构性因素，并将相应变换后的序列作为剔除内部结构性影响后的样本数据，以供后文进行复杂度综合测算。

根据重组和替代变换的步骤，对五个阶段内的深圳综合指数5分钟高频数据依次进行重组和替代变换后的多重分形度估计。结果显示，在2000年2月至2005年4月的第一阶段内，长记忆性是主要影响因素。其重组变换后序列的多重分形度平均低于原序列0.54，而替代变换后序列的多重分形度平均低于原序列0.19。在2005年5月至2007年9月的第二阶段内，依然是长记忆性为主要影响因素。其重组变换后序列的多重分形度平均低于原序列0.21，而替代变换后序列的多重分形度平均低于原序列0.66。在2007年10月至2009年3月的第三阶段内，无论长记忆性还是厚尾分布特征影响成分均显著增加，但厚尾分布特征的影响已超越长记忆性的影响。在2009年4月至2011年10月的第四阶段内，厚尾分布特征的影响力持续攀升。在2011年11月至2013年12月的第五阶段内，长记忆性与厚尾分布特征的影响程度相近，但相对来讲，长记忆性的影响略大。因此，笔者取第一、二、五阶段内经重组变化后的序列，第三、四阶段内经替代变换后的序列作为剔除序列内部结构性影响因素后的待估计数据。

四、股价波动复杂度的综合测算与演化分析

基于文献梳理和对内部结构性影响因素的剔除，本文选择通过两层面形成对股价波动复杂度的综合测算，即，基于小样本效应改进MF-DFA算法;将修正后的MF-DFA、基于兼容法的算法复杂度和模糊熵算法所形成的计算结果构造综合测度指标。

(一)股价波动复杂度的综合测度指标构建

1．小样本修正下的MF-DFA测算步骤

当时间序列长度不足时，小样本效应会导致虚假多重分形度计算结果。笔者在Kantelhart和Zschiegner(2002)提出的MF-DFA算法的基础上，借助马尔科夫转换多重分形模型(简称为MSM)，针对小样本效应对多重分形度(Δα)的求解进行了修正。其修正步骤为:

(1)对股指序列采用极大似然法估计MSM模型的各参数值;

(2)给定序列长度，利用MSM模型的参数构造模拟序列;

(3)使用MF-DFA法对序列进行分析，得到系列Δα值;

(4)计算上述系列Δα的均值，并将其作为修正值。

由于本文仅以小样本效应修正后的MF-DFA算法为计算工具，而不是进行专门的理论探讨，因此对修正的具体理论基础不再作进一步说明。感兴趣的读者可参见作者(2013)的前期成果。

2．基于兼容法的算法复杂度测算步骤

兼容法的测算步骤为:将股指时间序列X={x1，x2，…，xn}的最小值、最大值和均值点依次标记为a0=min(X)，a1=mean(X)和a2max(X);对序列落在区间［a0，a1］及［a1，a2］的点分别求均值，并继续分别取其各自中点，反复n1次至将原序列划分成N1=2n1个子区间;原序列中xi∈［ai，ai+1］，i=0，1，2，…，N，对应符号，于是原序列被转变为符号数为N1

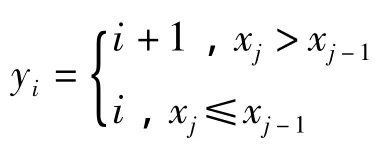
3．模糊熵复杂度测算步骤

股指序列模糊熵复杂度的计算公式可被定义为FuzzyEn(m，r，N)=lnXm(r)－lnXm+1(r)，其中X表示股指序列，关键参数为m，r，N，依次对应于相空间维数、相似容限度和序列长度。模拟检验表明，m的经验适宜取值为2或3，r的经验适宜取值为 ［0.3，0.35］，序列长度为1000－2000时的测度渐进稳定。模糊熵测度值越大，序列复杂度越大。依研究惯例，本文选择m和r的经验值为3和0.3。

4．测算结果的指标化与权重确定

为了综合反映上述各方法的测度结果，并降低数量级，本文运用极差标准化法对各测度结果进行形如式(1)的标准化处理。

对经标准化处理后的数据以等权加权求和，可得股价波动复杂度的综合测度指标值。为了便于后文计算与分析，笔者在此也对货币化程度数据进行形如式(1)的指数化处理，以便统一数量级。

(二)综合指标测算下股价波动复杂度估计结果与演化路径

以2000年1月深圳综合指数5分钟高频预处理后的数据序列作为滑窗的基础数据，以实际的月内交易天数作为滑窗步长求解各阶段内股价波动复杂度的月度值。经小样本效应修正和指标合成后，综合指标测算下各阶段和全样本区间内中国股价波动的复杂度结果如图2(1)－(6)所示。

对比综合指标测算值与三种测算方法各自的指标化结果可以发现，综合指标对上述三种方法的测算形成了较好的平滑;且综合指标值相对于三种测算方法下的结果并未产生突点，具有综合性和可信性。

从测算结果看，剔除时间序列内部结构性影响后，股价波动复杂度在全样本区间内整体逐步攀升，但在尾部有所减缓。在第一阶段(股权分置改革之前)，股价波动复杂度的均值为0.3219，方差为0.0086，复杂度值处于相对低位，且波动更多来自于向下降低复杂度的压力(如图2(1));在第二阶段(中国股市高度繁荣阶段)，股价波动复杂度均值为0.4013，方差为0.0147，波动性相对最高，说明此阶段内股价波动有较强提高复杂度的冲动;在第三阶段(受次贷危机冲击阶段)，股价波动复杂度均值为0.5083，方差为0.0079，复杂度值上升到高位但稳定性较差;在第四阶段(大量流动性注入阶段)，股价波动复杂度均值为0.5189，方差为0.0048，复杂度值处于相对最高位且波动平稳;在第五阶段(后危机时代)，股价波动复杂度均值为0.5065，方差为0.0067，复杂度值较前一阶段略有下降，但依然维持在相对高位。即，中国股价波动复杂度经历了从低位徘徊——上升冲动——高位波动——高位平稳——近期有所回落的演化过程。

五、中国货币化程度变迁与股价波动复杂度演化的耦合关系分析

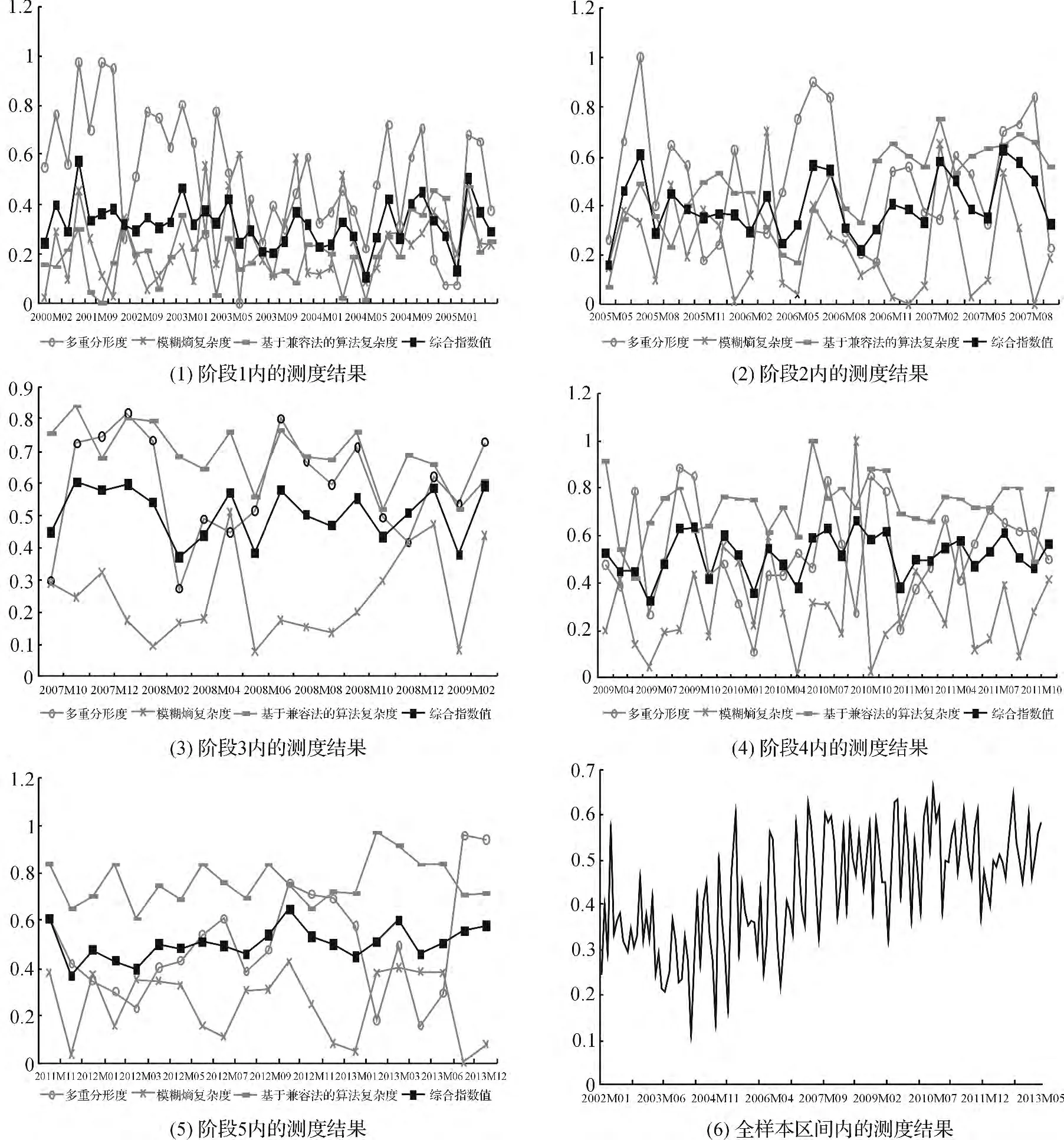
图2 中国股价各阶段波动复杂度的测度结果

耦合分析突破了对变量因果关系分析的范畴，能够以系统论的思想综合而全面的分析不同变量之间的协调与发展变动关系。鉴于既有文献鲜有关于货币化程度与股价波动复杂度耦合关系的研究，且耦合理论引入社会经济系统的成果主要集中于经济增长领域，本文在模型设定方面借鉴逯进、周惠民(2013)的研究，形成对中国货币化程度变迁与股价波动复杂度演化耦合关系的实证分析。

(一)耦合关系模型构建

1．系统结构设计

设f(x)=xi表示股价波动复杂度子系统的发展水平，其中，xi为综合测算指标下所得的股价波动月度复杂度值;g(y)=yi表征货币化程度子系统的发展水平，yi为经指标化后的货币化程度月度指标值。

2．耦合模型

对于系统协调度的表征，偏离差系数①偏离差系数表征两个变量之间的平均偏离值，可以衡量两个变量总体偏离45度射线的程度，偏离系数越小，表明两者偏差越小。Cv=可用于度量子系统间的协调程度。为了进一步增加不同研究主体的综合系统的可比性，逯进和周惠民(2013)将Cv表达式变形为，其中:

改进后以C值衡量子系统间的协调程度，C值越大协调度越好。对于系统发展度的表征，笔者借鉴Cobb-Douglas形式②本文假定系统的发展函数具有严格的拟凹性。:

其中，T表示股价波动复杂度和货币化程度两子系统组合所形成的总系统的发展水平，θ、1－θ分别反映二者相对于总系统的重要性。笔者假设两子系统对综合系统具有相同的重要性，即θ=0.5。

系统耦合度的衡量必然是对协调与发展两个维度的综合考量。协调线与发展线的交点形象描绘了综合系统的耦合水平，据此，由式(4)耦合度计算公式可以衡量股价波动复杂度和货币化程度两子系统的耦合关系。

其中，D为耦合度，其判别标准如表1所示。

表1 耦合程度的判别标准及划分类别

(二)实证结果

基于第四部分中指数化处理后的中国货币化程度指数数据和综合指标测算下的中国股价波动复杂度值，对每个阶段运用式(2)和(3)计算货币化程度和股价波动复杂度两子系统的协调度和发展度，并进一步运用式(4)计算“货币化程度－股价波动复杂度”综合系统的耦合度D(如图3)。

(三)耦合关系的动态变化

图3(1)－(5)的估计结果显示了各阶段耦合关系的具体演变路径。

1．股权分置改革前耦合关系濒临衰退

股权分置改革前，中国货币化程度变化平稳，股价波动复杂度相对最低。系统耦合度均值为0.4485，协调度均值为0.9181，发展度均值为0.2892，均属各阶段中的最低值。对应表3，说明这一阶段系统存在协调但频临衰退的关系。协调度看似较高但发展度极低的事实，说明中国股市在此阶段的发展主要依赖于货币化程度，但可能由于制度性缺陷等原因，股市效率不能得到较好的提升。

图3 中国货币化程度与股价波动复杂度耦合关系分阶段实证结果

2．股市高度繁荣时期耦合关系初步协调发展

在中国股市高度繁荣阶段，货币化程度变化平稳，股价波动复杂度居中但波动性相对最高。耦合度基本稳定于0.4－0.6之间，说明此时中国货币化程度与股价波动复杂度之间存在勉强而初步的协调发展关系。就协调度而言，C值在2007年前较接近于1，而到2007年出现较为明显的大幅下降，说明在中国股市繁荣的初、中期，货币化程度与股价波动复杂度之间存在较高的协调性;而在股市繁荣的尾声阶段二者协调性快速回落，股市的后期高速发展超出了货币化程度的限能，这恰与当时中国股市临近由高度繁荣转向大幅下跌的实际情况相吻合。就发展度而言，T始终在0.2－0.4的低位数值带内较平稳的运行。协调度高但发展度低的结果说明，此阶段内股市的繁荣主要依靠货币的推动，而股市效率并没有能够随货币深化程度的提高而加强。

3．次贷危机冲击阶段耦合关系呈现反转

在受到危机冲击的阶段，系统耦合度、协调度和发展度都呈现为初期的大幅下跌和后期的快速上升。即，受金融危机影响而致使价格大幅下跌时，货币化程度与股价波动复杂度的关系有所疏松;而在股市回升阶段又与货币化程度形成密切联系;当中国货币化程度加速回升时协调、发展和耦合程度均快速上升，并在最终数值较上一阶段实现了大幅跃升。图3(3)显示时间拐点恰与我国推出系列经济刺激政策和对市场流动性注入的时间点相吻合。

4．大量流动性注入时期的中级协调发展

在大量流动性注入阶段，货币化程度高位平稳，股价波动复杂度均值达样本内最大，波动性为样本内最低，耦合度的均值为0.7523，方差为0.0021。对应表1，此时中国货币化程度与股价波动复杂度之间存在中级协调发展关系。协调度的均值为0.9739，方差为0.0011，数值和平稳性均位居各阶段之首;发展度的均值为0.5822，方差为0.0011，数值和平稳性均仅次于第五阶段。说明在危机过后和大量流动性的注入及消化阶段，中国股市仍较强的依赖于货币资金，但较以往不同的是，在货币深化的同时股市效率有所提升。

5．后危机时代耦合关系实现平均相对峰值与回落性波动并存

后危机时代，货币化程度快速上升并在尾部趋于平缓，股价波动复杂度相对较高但波动较为平稳。实证结果显示，在该阶段内耦合度的均值为0.7603，方差为0.0019，达到演化过程中的相对峰值。对应表1，虽仍属中级协调发展关系，但中国货币化程度与股价波动复杂度两子系统在此阶段达到了演化以来最高的共同发展程度。同时值得注意的是，系统协调度在此阶段的中期位置出现了小幅下降(如图3(5)所示)。而其时间点恰与2013年中国银行间系统资金紧缺的时间相匹配。在资金紧缺风暴后，协调性虽然得到回升，但相对初期值仍有所降低。说明新形势下股价波动复杂度与货币化程度之间关系的紧密程度已开始下降。综合来讲，其意味着在演进过程中，中国股市的市场效率已逐渐能够在货币深化的同时得到提升，而对货币资金的单纯依赖性开始弱化。

中国货币化程度变迁与股价波动复杂度演化的进程并非一蹴而就，其耦合关系经历了初期的濒临衰退、勉强协调发展、初步协调发展、特殊时期耦合关系的反转以及危机冲击后不断上升的中级协调发展的历史演变过程。从演化路径的适宜性跃迁角度看，由于时至目前，中国货币化程度与股价波动复杂度之间的耦合关系仍未能达到优质甚至良好协调发展状态，尤其是发展度还存在较大提升空间，可在进一步提升货币化程度与股价波动复杂度二者的发展程度后相应提升协调度，形成旋进发展的提升路径。

六、结论与启示

本文着重梳理了中国货币化程度变迁与股价波动复杂度间的演化关系，在对主流复杂度测算方法形成改进的同时，构造系统指标对中国股价波动复杂度进行了综合测算。筛选并剔除影响时间序列复杂度的内部结构性因素后，基于耦合模型实证检验了中国近10余年来货币化程度与股价波动复杂度间的协调演进关系，并对耦合度等相关变量的演化规律进行了分段化研究，形成如下主要结论:

第一，本文所构建的股价波动复杂度综合测算指标能够在修正小样本效应的同时对主流测算方法形成较好的平滑与融合，具有综合性和可信性。

第二，剔除序列内部结构性影响因素后，股价波动复杂度随时间推移而整体上升，且在危机冲击后的流动性大量注入阶段得到了快速跃升。

第三，虽然中国货币化程度与股价波动复杂度的耦合关系在演变过程中存在阶段性变迁，但耦合度依然呈现了整体上升。在协调与发展双重推进的作用下，耦合关系经历了由濒临衰退，勉强协调发展，初步协调发展，到特殊时期耦合关系的反转，再到危机冲击后不断上升的中级协调发展的演变路径。大量流动性的注入促使货币化程度对股价波动复杂度形成了强影响。目前中国货币化程度与股价波动复杂度的耦合度尚处较低水平，其值仍未能达到优质甚至良好协调发展关系的标准。

［1］ Allen F，Carletti E ＆ Gale，D．Money，financial stability and efficiency［J］．Physical A，2014，149(1):100－127．

［2］赵进文．资产价格波动对中国货币政策的影响——基于1994－2006年季度数据的实证分析 ［J］．中国社会科学，2009，(2):98－114．

［3］汪寿阳，张维，李心丹，部慧．复杂金融系统工程与风险管理研究的新进展［J］．系统工程理论与实践，2011，(4):1－4．

［4］张文．经济货币化进程与内生性货币供给——关于中国高比率的货币分析［J］．金融研究，2008，(2):13－32．

［5］李稻葵，张双长．V型反弹，资产泡沫与新宏观分析框架——金融危机后宏观经济形势分析与展望［J］．经济学动态，2009，(9):3－14．

［6］芮国胜，张嵩，孙文军，张洋，崔文．混沌震荡系统的空时复杂度［J］．数学的实践与认识，2011，(18):123－129．

［7］ Francisco O＆Araceli N．Empirical fractal geometry analysis of some speculative financial bubbles［J］．Physica A，2012，391(12):5132－5138

［8］黄超，龚惠群，仲伟俊．基于多重分形聚类的证券市场指数波动性比较研究［J］．管理科学，2010，(3):88－95．

［9］ Wei-Xing Zhou．Finite-size effect and the components of multifractality in financial volatility ［J］．Chaos，Solitons＆ Fractals，2012，45(2):147－155．

［10］ Ladislav Kristoufek．Measuring correlations between non-stationary series with DCCA coefficient［J］．Physica A，2013，(10):1－10．

［11］ Guangxi Cao，Longbing Xu＆Jie Cao．Multifractal detrended cross-correlations between the Chinese exchange market and stock market［J］．Physica A，2012，391(5):4855－4866．

［12］ Richman J＆ Mooeman J．Physiological time-series analysis using approximate entropy and sample entropy［J］．Am．J．Physics，Heart Circ Physics，2000，278(6):2039 －2049．

［13］ Hongtao Chen＆ Chongfeng Wu．Forecasting volatility in Shanghai and Shenzhen markets based on multifractal analysis［J］．Physica A，2011，390(4):2926－2935．

［14］孙克辉，贺少波，尹林子，阿地力多力坤．模糊熵算法在混沌序列复杂度分析中的应用［J］．物理学报，2012，(13):130507．

［15］ Barunik Jozef，Aste Tomaso，Di Matteo T＆Liu Ruipeng．Understanding the source of multifractality in financial markets［J］．Physica A，Statistical Mechanics and its Applications，2012，88(17):174102．

［16］周炜星．上证指数高频数据的多重分形错觉［J］．管理科学学报，2010，(3):81－85．

［17］逯进，周惠民．中国省域人力资本与经济增长耦合关系的实证分析［J］．数量经济与技术经济研究，2013，(9):3－19．