模糊PID控制在船舶动力定位系统中的应用

陈珊珊

(重庆电子工程职业学院，重庆401331)

0 引 言

船舶在深海中由于受到风、波浪、海流等外力干扰，锚泊系统往往难以发挥其保持船位的作用。船舶动力定位系统可通过其控制系统驱动推进器来抵消环境外力，有效保持船舶在确定位置上或沿着预期的航迹行驶。动力定位系统一般包括推力系统、控制系统和位置测量系统3个部分。位置测量系统通过传感器实时地检测船舶实际位置与预设位置的偏差信号，并将偏差信号送给控制系统，控制系统结合环境外力计算出船舶恢复到预设位置需要多大的推力，从而对船舶各推力器进行推力分配，使船舶有效地保持在确定的位置上或沿着预期的航迹行驶［1］。图1 是动力定位系统示意图。

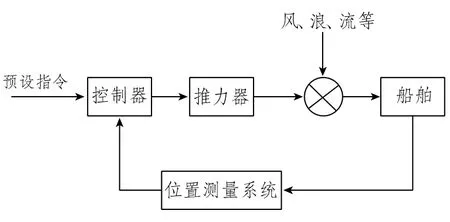
图1 动力定位系统框图Fig.1 Block diagram of dynamic positioning system

1 船舶三自由度模型

船舶在海平面上是关于6 种自由度高频和低频混合的复杂运动，而动力定位系统只考虑横荡、纵荡和首摇3 种自由度的运动。为了更方便地描述船舰运动状态，本文建立以船舶重心O 为原点、平行于船体基线方向为x 轴以及平行于基面指向右舷为y 轴的随船坐标系xOy和以大地上的G 为原点的大地坐标系XGY。

船舶三自由度的数学模型很多种形式，本文仅列写出一种比较常用的形式:

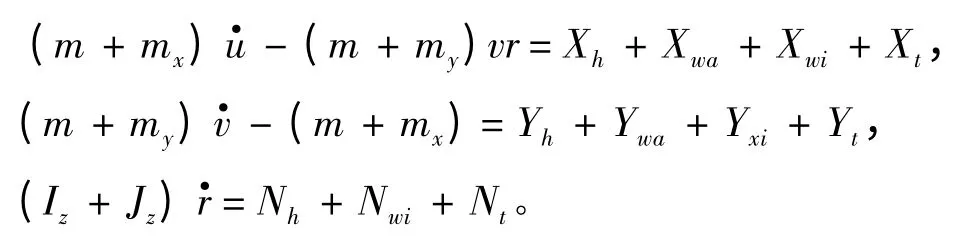
式中:m 为船舶的质量;my和mx分别为船舶在横荡和纵荡方向运动中产生的附加质量;u和v 分别为随船坐标系原点的线速度矢量在x和y 轴上的投影;为首向角的变化率;X和Y 分别为纵荡和横荡方向的力;N 为首向的力矩;Xt，Yt，Nt分别为三自由度方向上的推力;Iz为船纵向的附加转动惯量;Jz为船横向的附加转动惯量;下标h，wa，wi，t 分别为船体的水动力、波浪飘力、风力和推进器推力［2］。

水动力系数和惯性矩阵为:

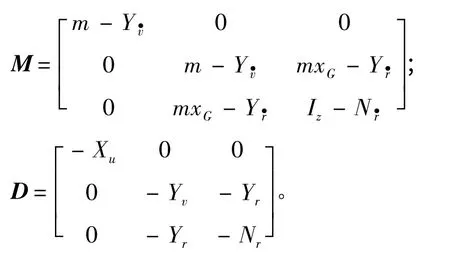
假设阻尼是线性的，考虑水动力的影响，可得到船舶的动力定位模型:

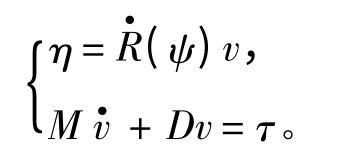
式中:τ=BU，B 为描述推进器配置的控制矩阵，U为控制输出。

2 控制器设计

针对船舶的三自由度数学模型，本节对动力定位系统中的模糊PID控制进行详细设计，图2 为动力定位系统控制结构框图。

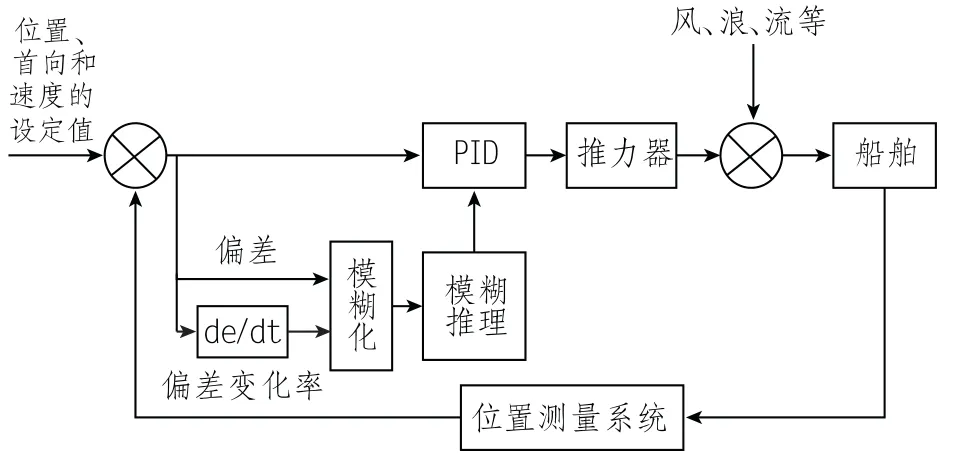
图2 动力定位系统控制结构框图Fig.2 Block diagram of controller of dynamic positioning system

针对三自由度纵荡、横荡和首摇运动，本文分别设计3个独立的模糊PID控制回路。以纵荡运动为例，选取船舶位置的预测输出误差E 及其误差变化率EC 作为模糊PID控制的输入，选取Kp，Ki，Ku作为模糊控制的输出［3］。利用模糊控制规则，在线对船舶三自由度PID 参数进行修改，以满足不同E和EC 时对控制参数的不同要求。由于其模糊分割数为7，故将E和EC 分为7个模糊子集:正大(PL)、正中(PM)、正小(PS)、零(Z0)、负小(NS)、负中(NM)、负大(NL)。即:

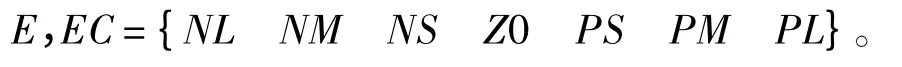
将Kp，Ki，Kd分为4个模糊子集:大(L)、中(M )、 小 (S )、 零 (Z )。 即: Kp，Ki，Kd={Z S M L}。E和EC的论域均取为［-6 6］，对应的模糊论域为:

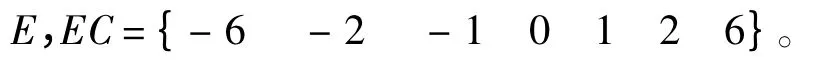
为了方便计算且占用内存小，本文输入、输出模糊集的隶属函数均选取为三角形，它可近似地反映E和EC 输入的隶属关系。相邻三角形隶属函数的顶点和起点对应，图3 为隶属函数的分布曲线。

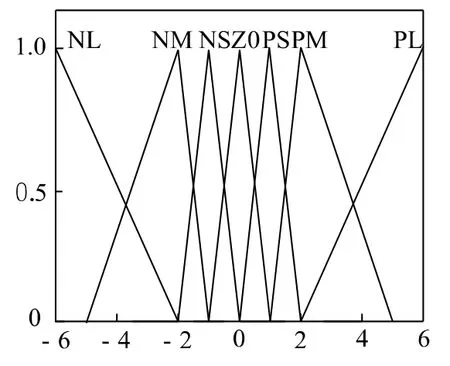
图3 E和EC 隶属函数分布曲线Fig.3 The distribution of the E and EC of the membership function curve

同理，模糊推理机输出Kp，Ki，Kd的隶属函数分布曲线如图4～图6所示［4］。

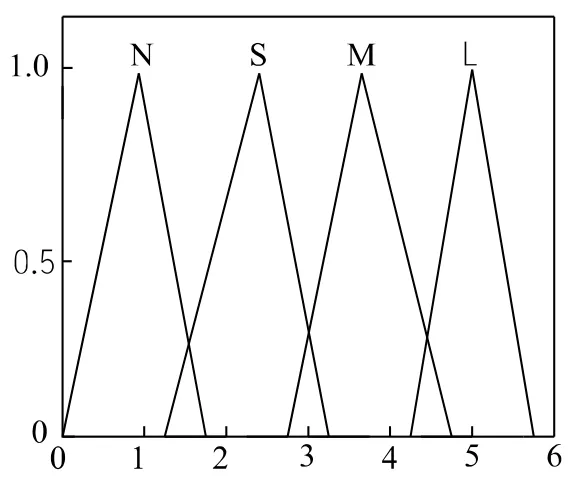
图4 Kp 隶属函数分布曲线Fig.4 The distribution of the Kp of the membership function curve

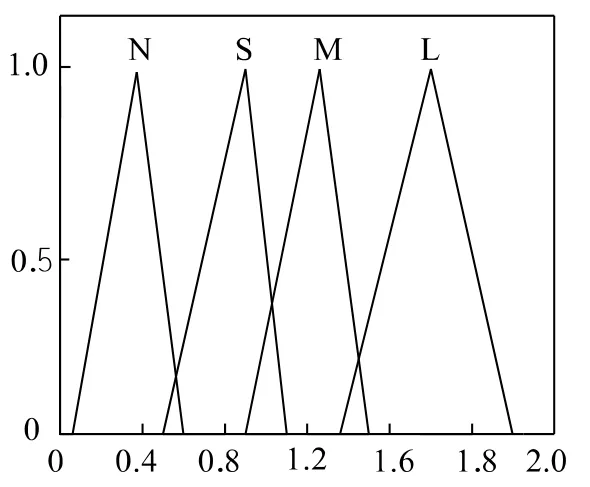
图5 Ki 隶属函数分布曲线Fig.5 The distribution of the Ki of the membership function curve

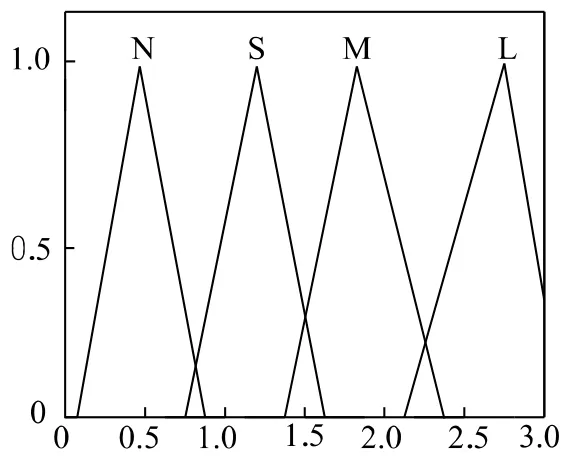
图6 Kd 隶属函数分布曲线Fig.6 The distribution of the Kd of the membership function curve

在以上模糊化处理的基础上，本文根据控制经验，将模糊条件语句制成关于纵向控制器推力F的控制规则表。

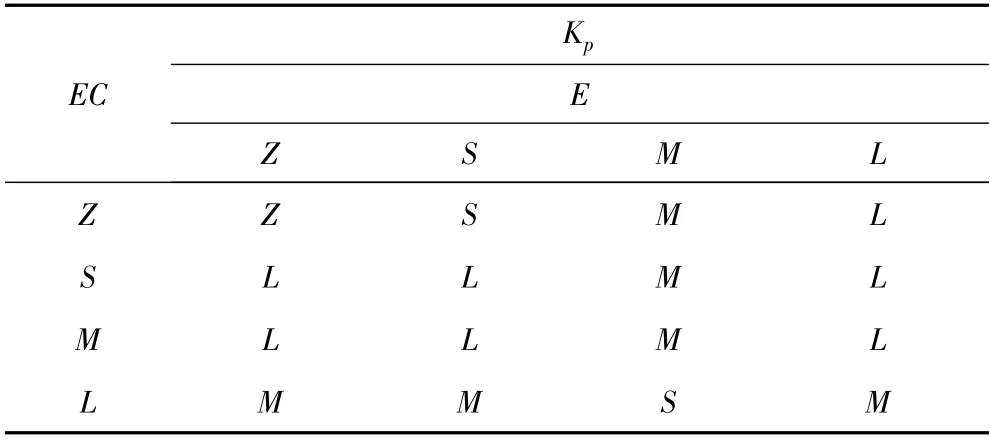
表1 Kp 值控制规则表Tab.1 Grid of Kp＇s value of control rule

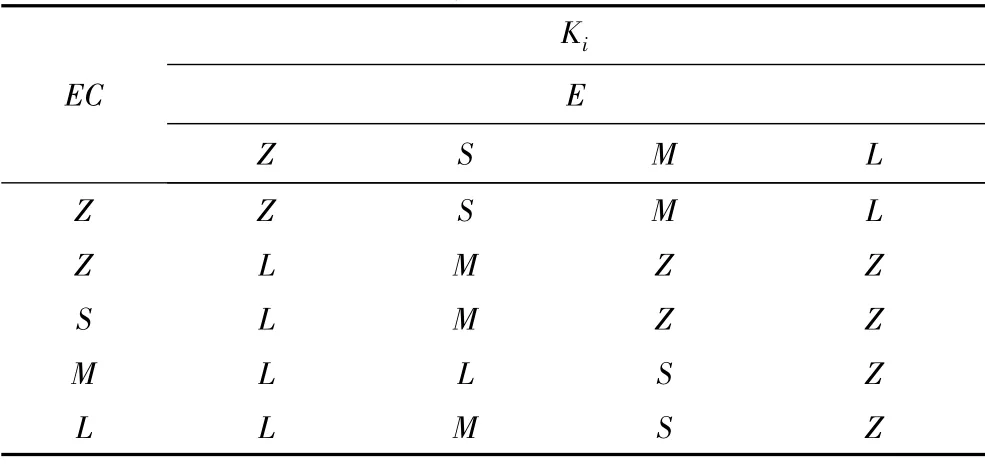
表2 Ki 值控制规则表Tab.2 Grid of Ki＇s value of control rule

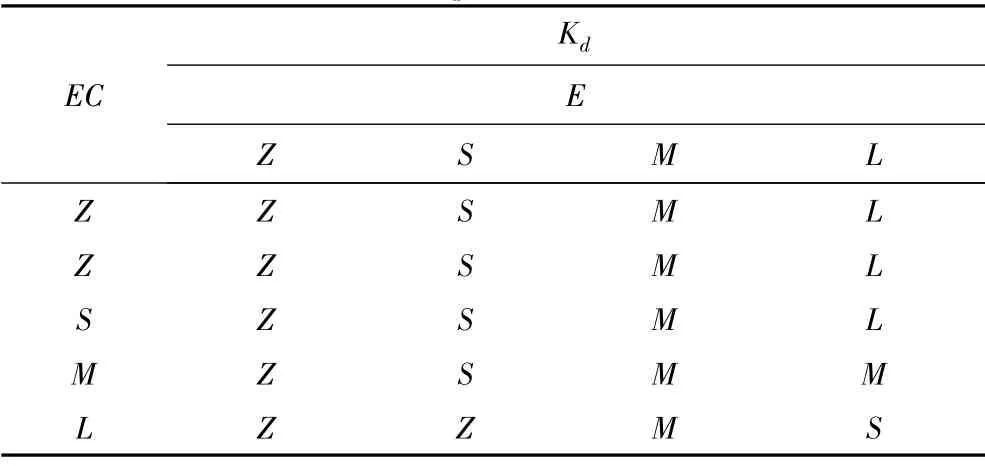
表3 Kd 值控制规则表Tab.3 Grid of Kd＇s value of control rule

将上述规则表以一系列“IF- THEN”语句形式存入模糊控制器的知识库中。当位置测量系统输入位置误差及其变化率时，通过查询知识库，输出Kp，Ki，Kd作为控制决策，完成对船舶三自由度PID3个参数的自整定。

3 结 语

利用Matlab7.4 软件自带的模糊逻辑工具箱Fuzzy搭建整个模糊PID控制系统模型，对系统输入阶跃函数(step=5)，得到整个系统的仿真波形如图7所示。

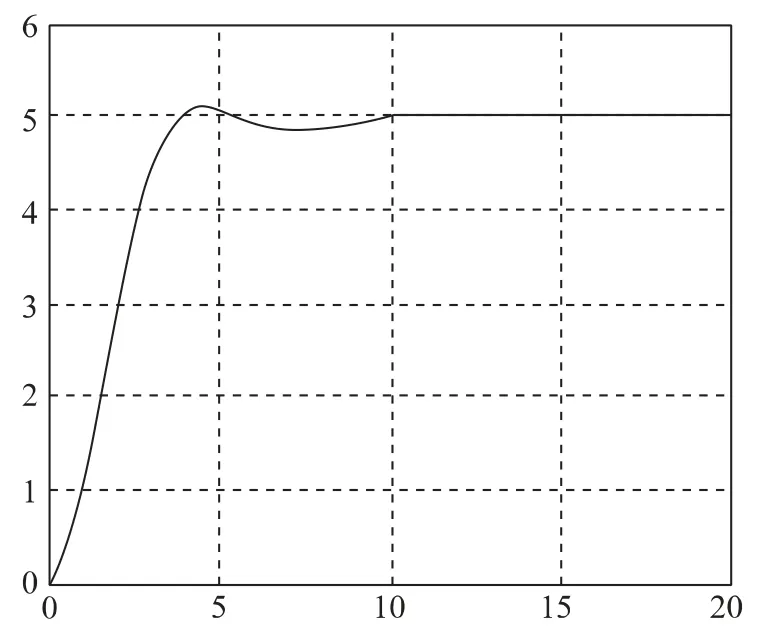
图7 纵荡运动时控制器仿真波形Fig.7 The simulation waveform of longitudinal controller when ship surging

由图7 动力定位系统控制器仿真波形可知，将模糊控制与PID控制相结合的方式既规避了PID控制依靠数学模型，控制存在误差信号相位滞后，控制参数难以整定和事后控制等缺点，又规避了模糊控制依靠单纯的人为经验等缺点。利用模糊控制先进的专家系统，实现PID 参数的自整定，所设计的智能控制器控制品质高，鲁棒性强，能对船舰进行有效定位。

［1］卢佳佳，俞孟蕻，韦华，等.变吃水船舶动力定位控制策略［J］.舰船科学技术，2013，35(8):76-80.LU Jia-jia，YU Meng-hong，WEI Hua，et al.Research on changeable draft ship dynamic positioning control strategy［J］.Ship Science and Technology，2013，35(8):76-80.

［2］徐阳，俞孟蕻.船舶动力定位系统模糊PID控制算法研究［J］.中国舰船研究，2008，3(4):68-71.XU Yang，YU Meng-hong.Research on fuzzy PID control algorithm of shipping dynamic positioning system［J］.Research on Ship China，2008，3(4):68-71.

［3］郭敏.基于模糊控制理论的船舶动力定位系统的研究［J］.武汉船舶职业技术学院学报，2012(3):26-30.GUO Min.On ship DP control system designing based on fuzzy control theory［J］.Journal of Wuhan Institute of Shipbuilding Technology，2012(3):26-30.

［4］王猛.模糊PID控制方法在船舶动力定位系统中的应用研究［D］.武汉:武汉理工大学，2013:21-32.WANG Meng.Research on the application of fuzzy PID control method in the ship dynamic positioning system［D］.Wuhan:Wuhan Vniversity of Tochnology，2013:21-32.

［5］杨金节，俞孟蕻，李晨曦，等.船舶动力定位系统多模型自适应融合滤波［J］.舰船科学技术，2014，36(8):37-41.YANG Jin-jie，YU Meng-hong，LI Chen-xi，et al.Multiple model adaptive fusion filtering for dynamic positioning of marine vessels［J］.Ship Science and Technology，2014，36(8):37-41.