基于QFD和Kano模型的合作伙伴的选择

曾佑新，王 莉

（江南大学 商学院，江苏 无锡214122）

在中国经济进入新常态的背景下，开展供应链管理（SCM）是企业提高管理水平和提升产业发展质量的重要途径。供应链管理模式通过在供应链节点企业间建立合作伙伴关系来实现物流、信息流、资金流三流的有效传递，最终达到满足消费者需求的目的。［1］合作伙伴关系是企业之间通过并行工程、信息共享、风险分担、群体群策等方式建立起的一种“双赢”的合作关系，它是现在供应链管理研究的重点内容。因此供应商、制造商、分销商、零售商和消费者等供应链节点企业如何选择以共商务、共竞争和双赢为基础的合作伙伴是实施供应链管理的重要环节。

供应链合作伙伴的选择方法相当繁多，经过对目前已有文献的搜集整理，主要有博弈分析法、等级分评定法、层次分析法（AHP）、模糊评判法和逼近理想解排序法（TOPSIS）等五种方法。虽然供应链企业合作伙伴的选择方法体系非常庞大，然而每种方法都有其固有的缺陷，不可能解决所有问题，未达到最佳的效果［2］。

首先现有方法体系对具体产品的针对性不强，没有充分考虑顾客需求，而且很多指标都是依据决策者的定性判断，评判结果具有很强的主观性。而质量功能展开法从顾客需求出发，将抽象的顾客需求转变为产品的工程特性，提高了对产品的针对性，［3］而且工程特性一般有通用的量化表示，这使得决策结果更加客观公正，易于认可与推广。

其次现实生活中，针对不同类型的顾客需求，在满足程度相同的情况下，经计算得到的顾客满意程度往往不同。Kano模型将顾客需求分为五大类，采用Kano系数修正工程特性值，有效解决了顾客需求度与满意度不一致的问题。

再次在质量屋结构中，顾客需求的权重、各工程特性间的关系、顾客需求与工程特性间的关系等定性指标都无法得到具体的数据，只能根据专家的打分来判断，具有很大的主观性。因此本文采用模糊数里的三角函数和区间数来表示，专家只需根据具体情况给出相应等级，而不必具体打分。

因此，本文将一些互补的方法结合起来使用，在对已有文献研究的基础上，通过分析比对，最终选择了基于QFD和Kano模型的模糊非线性合作伙伴选择方法，运用QFD方法将抽象的顾客需求转化为直观的工程特性，引入Kano模型将工程特性根据重要程度进行分类，并采用三角模糊数和区间数对数据进行加工处理，Kano模型和模糊数理论集成起来对合作伙伴进行选择，很好的弥补了每种方法单独使用的不足，有效保证了研究结果的科学性和权威性。

一、相关理论和方法

1.QFD理论

质量功能展开QFD（Quality Function Deployment），简单的从字面上理解：质量（Q）——顾客的需求，功能（F）——如何满足顾客需求，展开（D）—将其运用到整个系统中。QFD有三种常见的应用模式，［4］分别为日本综合 QFD模式（赤尾模式）、ASI（美国供应商协会）模式（四阶段模式）和GOAL／QPC模式，其中第二种模式简明易懂，便于操作，因此成为目前学者研究和企业采用的主流模式，本文也将采用此模式进行研究。

QFD的核心工具是质量屋（HoQ），由七个矩阵构成，［5］其结构如图1所示。

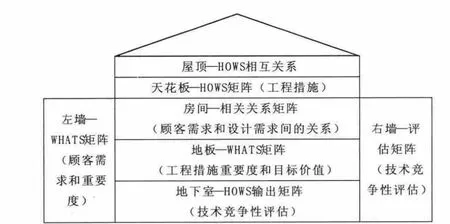
图1 质量屋的典型结构Fig.1 Typical structure of HoQ

（1）左墙：顾客需求（WHATs）输入项矩阵。表示顾客的需求是什么，包括顾客需求及其重要度（权重）两部分，是顾客的语言（Voice of Customers）。其中顾客需求是指顾客对产品或服务的具体的质量要求；顾客需求重要度是指各项需求对顾客的重要程度。获取顾客需求是进行质量功能展开的第一步，也是至关重要的一步，由相关人员选择合适的顾客对象，利用询问、问卷调查等方式获取尽量准确、完整的顾客需求及其重要度（权重），然后对调查结果进行筛选、归纳与整理。

（2）天花板：技术特性（HOWs）矩阵。表示针对顾客需求应该如何去做，包括工程措施或技术需求，是工程设计人员的语言（Voice of Engineers）。技术特性是指由顾客需求转化而来的可操作的工程特性或措施，即如何满足顾客需求。

（3）房间：相关关系矩阵。表示顾客需求与设计需求之间的相关关系，是质量屋的核心内容，反映了顾客需求到技术特性的一种映射。

（4）屋顶：技术特性（Hows）的自相关矩阵。表示各个技术特性之间的相互关系。每个技术特性都不是独立存在的，它们之间相互影响，在确定具体的技术参数时，不能片面的仅仅根据各工程特性的重要程度，还应综合考虑其他工程特性对其的影响。QFD用正相关、不相关和负相关3种方式来表示各工程措施之间的关系。

（5）地板：技术特性（Whats）矩阵。表示各技术特性的成本评估，包括工程措施的重要度及其目标值两部分。通过顾客需求重要度和相关关系矩阵可以得到技术特性矩阵。工程措施重要度可用来确定关键措施，找出技术瓶颈，以便在后续工作中明确方向，提高生产效率。

（6）右墙：评估矩阵。表示从顾客角度进行可竞争力、竞争性或可行性分析比较，包括市场竞争性评估、企业产品评价、竞争对手产品评价和改进后产品评价四个方面。通过顾客对本企业的产品和竞争对手相似产品的客观评价来取长补短，寻找企业更为合适的发展领域。

（7）地下室：Hows输出项矩阵。表示从企业自身角度进行技术竞争性评估。企业内部相关人员对本企业和竞争对手在各个工程特性上的技术水平做出评价。

以上为质量屋的基本构架，通过市场调研输入顾客需求的信息，经过定性和定量的评价，输出有关技术特性的信息，最终实现“需要什么（Whats）”到“如何操作（Hows）”的转化。

2.Kano模型

Kano博士根据质量特征与顾客满意之间的不同关系，从产品的质量角度，将产品的质量分为五种不同等级的质量，同样从顾客需求的角度进行考虑，也可以划分为五种顾客需求，如图2所示。

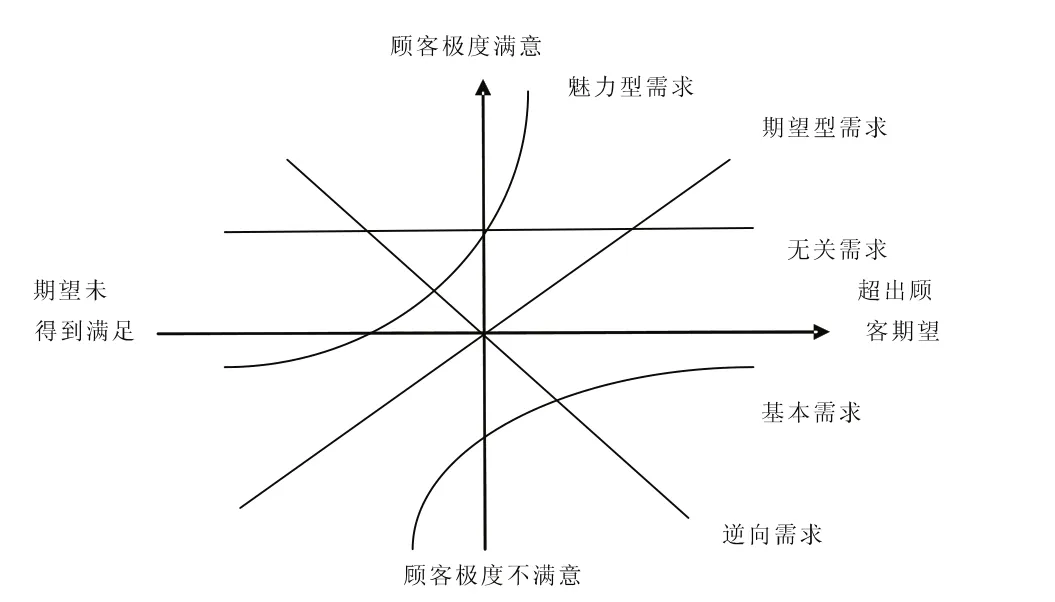
图2 Kano模型Fig 2 Kano model

（1）基本需求（Must-be requirements）：该需求是顾客认为产品或服务必须具备的特性或功能。

（2）期望型需求 （One-dimensional requirements）：该需求是顾客期望通过产品或服务得到满足的需求。

（3）魅力型需求（Attractive requirements）：该需求是顾客意想不到却被满足的需求，是会给顾客带来惊喜的需求。

（4）逆向需求（Reverse requirements）：该需求是指那些顾客不希望得到满足的需求。

（5）无关需求（Indifferent requirements）：该需求是顾客不关注的一类需求，这类需求无论是否提供，也无论其满足程度如何，都不会对顾客的满意度产生任何影响。

这五类顾客需求中，前三类是企业在产品或服务的设计和生产全过程需要重点考虑的。其中，基本需求是企业在产品或服务开发过程中应达到的基本标准，期望型需求决定了企业在市场竞争中的服务差异化定位，魅力型需求则为企业的创新活动指明了发展方向。

3.三角模糊数

假定模糊集S是一个正则凸集，有且仅有一个x0，使得us（x0）＝1，且us（x0）是连续函数，则模糊集S的表达式为：

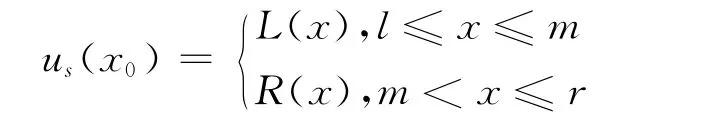
其中，L（x）为单调增函数，R（x）为单调减函数。若L（x）和R（x）均是线性函数，并且0≤L（x）≤1，0≤R（x）≤1则模糊集S便成为三角模糊数，如图3所示。

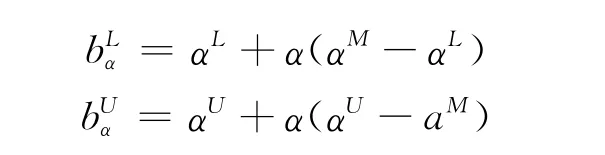
图3 三角模糊数形式Fig 3 Form of triangular fuzzy number

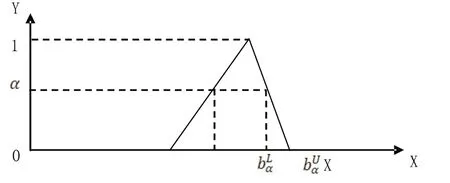
图4 三角模糊数的α-截集及其左右边界Fig 4 α-cut of triangular fuzzy number and its left and right sides of border

Zadeh（1975）提出用模糊语义的方式对人类的语言程度进行描述。常用的语言标度为5级与9级之间，这也是心理学家Miller所推荐的。本文采用5级语言标度，将一系列评价结果分为五个等级，设定模糊集合 U＝｛VL，L，M，H，VH｝，其中，VL＝非常低，L＝低，M＝中等，H＝高，VH＝非常高，对应的三角模糊数和模糊语言标尺如表1和图5所示。

表1 三角模糊数Tab 1 Triangular fuzzy number

图5 模糊语言标尺（5级）Fig 5 Fuzzy language scale（level 5）

二、供应链合作伙伴选择的评估模型

针对已有的供应商选择方法体系中存在的不足，本文采用基于质量功能展开和卡诺模型的模糊非线性方法对其进行改进［6］。现将该模型的具体构建过程作详细描述：

1.定义参数

将文中用到的参数作如下定义：

Sr——第r个供应商；

CRi—— 第i个顾客需求，i＝1，2，…，I；

ECj—— 第j个工程特性，j＝1，2，…，J；

Xr，j——Sr产品在ECj上的值；

Pr——考虑Kano模型时Sr的总得分。

2.评估模型公式

在供应商合作伙伴选择模型的建立和推导过程中，需要用到一系列相关联的基本公式，现作如下列示：

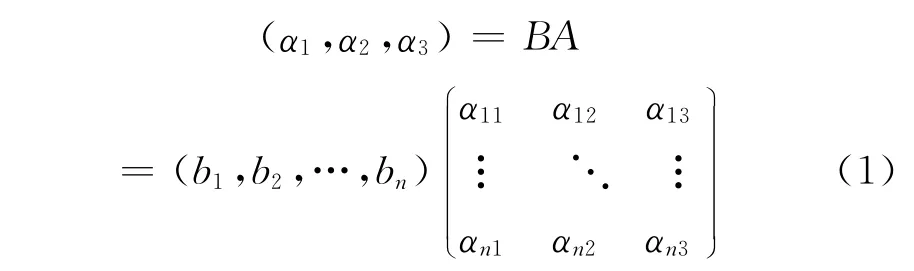
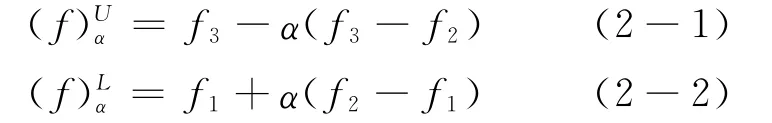
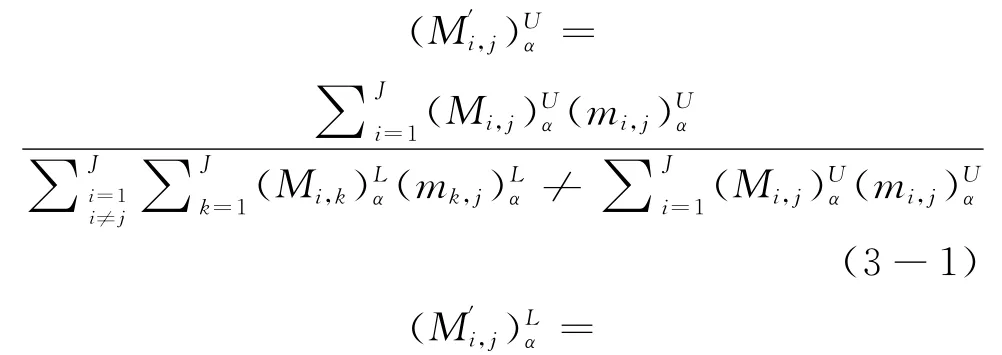
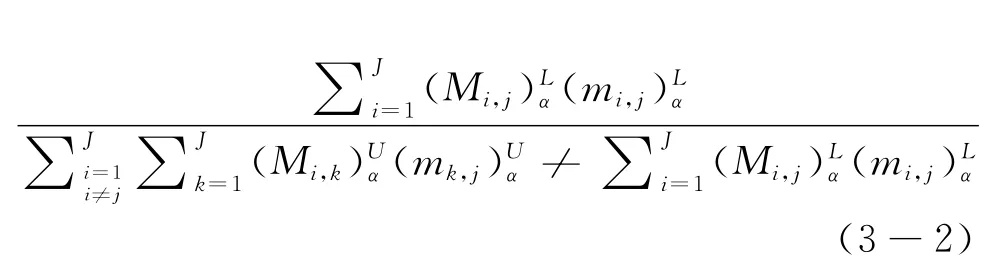
标准化后的CR-EC间相关关系以及CR的权重共同确定工程特性EC的权重，［8］公式如下：

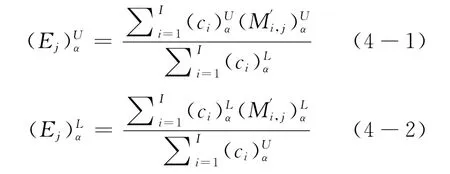
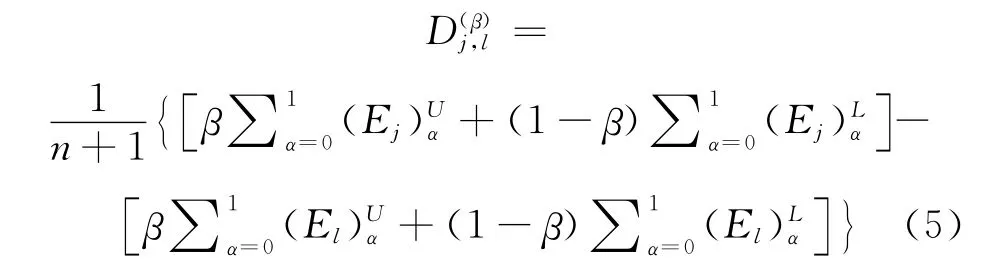
其中，n表示α的取值个数，n为大于1的整数；β在0与1之间取值，代表决策者的偏好，如当β＝0.5时，表示决策者保持中立的决策态度。

当采用Kano模型后，供应商Sr的最终总得分为

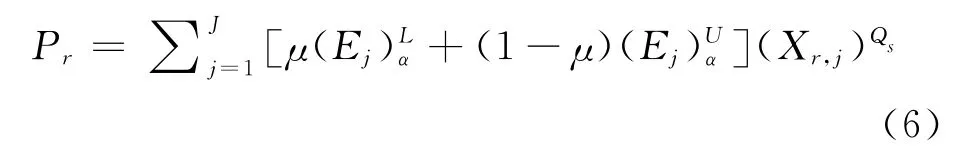
其中，Qs为 Kano系数，s＝1，2，3，而 ，Q1，Q2，Q3分别代表基本需求、期望需求和魅力需求；μ为将三角模糊数精确表示时的系数，在0到1之间取值，其具体值由决策者决定。［11］

3.评估模型的流程

（1）确定CR集合。

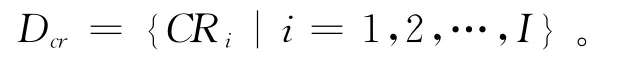
（2）确定EC集合。

各供方企业在充分考虑需方企业在质量、时间、成本、服务等方面需求的基础上，结合顾客需求因子和企业自身情况，罗列出所有工程特性因子，然后经过多轮分类与整合，最终确定与所有顾客需求因子CR相关联的工程特性因子EC，这些工程特性因子共同构成EC集合

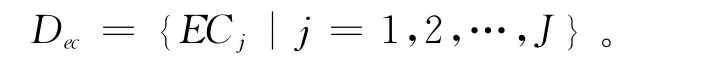
（3）确定CR的相对权重。

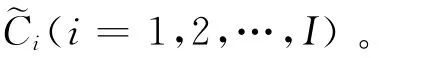
（4）确定EC间的相关矩阵。

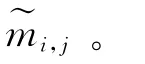
（5）确定CR-EC关系矩阵。

仿照上两步，首先有资深专家组确定出各项CR和EC间的关联等级，再根据公式（2-1）和（2-2）计算出，最后利用公式（3-1）和（3-2）对其标准化，得到和

（6）计算EC的相对权重并对其分类。

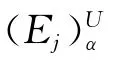
（7）确定 Xr，j的值。

通过市场评估调研，获得供应商Sr在各工程特性 ECj上的值Xr，j。

（8）计算供应商最终得分。

根据公式（6）计算各供应商的最终总得分。

（9）对计算结果进行敏感性分析。

由于公式（6）中将三角模糊数精确化时的系数是由决策者确定的，为避免决策者的主观随意性对计算结果造成影响，对其进行敏感性分析，使μ分别取0，0.1，0.2，…，1，根据公式（6），计算出 μ取不同值时各供应商的最终得分，验证供应商的排序结果是否会随着μ的取值不同而不同。

三、实证分析

为了验证上述方法的合理性和可操作性，使得本文的研究更具推广价值和实践意义，现以河南省中联玻璃有限责任公司为例进行具体的实证分析。

河南省中联玻璃有限责任公司（以下简称H公司）是一家集玻璃生产加工、批发、销售于一体的国有企业，石英砂为玻璃生产与制造过程中最基础最主要的原材料，因此H公司不可避免的要与石英砂供应商打交道，H公司在对石英砂供应商选择时，首先进行供应商初选，H公司在收集了大量石英砂供应商资料的基础上，结合德尔菲方法，由多位权威专家筛选出最适合的8个供应商做进一步评估，这些供应商分别为长兴晶鑫石英砂有限公司、安徽永鑫石英粉体有限责任公司、英德信和祥石英砂厂、北海市福来成石英砂有限责任公司、北京沃特利源环保科技有限公司、巩义市水处理材料有限公司、巨龙石英砂厂、成都茂岩矿业有限公司，为方便表达，以下分别用S1，S2，…，S8表示。

经过专家讨论和市场需求分析，H公司确定出5个需求因子，分别为文化兼容性（CR1）、财务稳定性（CR2）、地理位置（CR3）、管理的兼容性（CR4）、核心竞争力（CR5）。接下来该公司罗列出所有与顾客需求相关的工程特性，通过归纳与整理，最终确定考核供应商指标的5个工程特性因子，如表2所示。

表2 供应商工程特性整合表Tab 2 Integrated table of supplier engineering characteristics

完整的工程特性整合后的工程特性送货准确率送货准时率柔性送货能力ERP系统的完善程度交货能力（EC3）人力资源管理能力企业文化自然地理环境财务状况政治法律环境环保水平组织协调能力售后服务能力企业综合能力（EC4）新产品研发能力产品设计能力生产设备技术水平科技创新与发展潜力生产能力（EC5）

该问题的质量屋如图6所示：

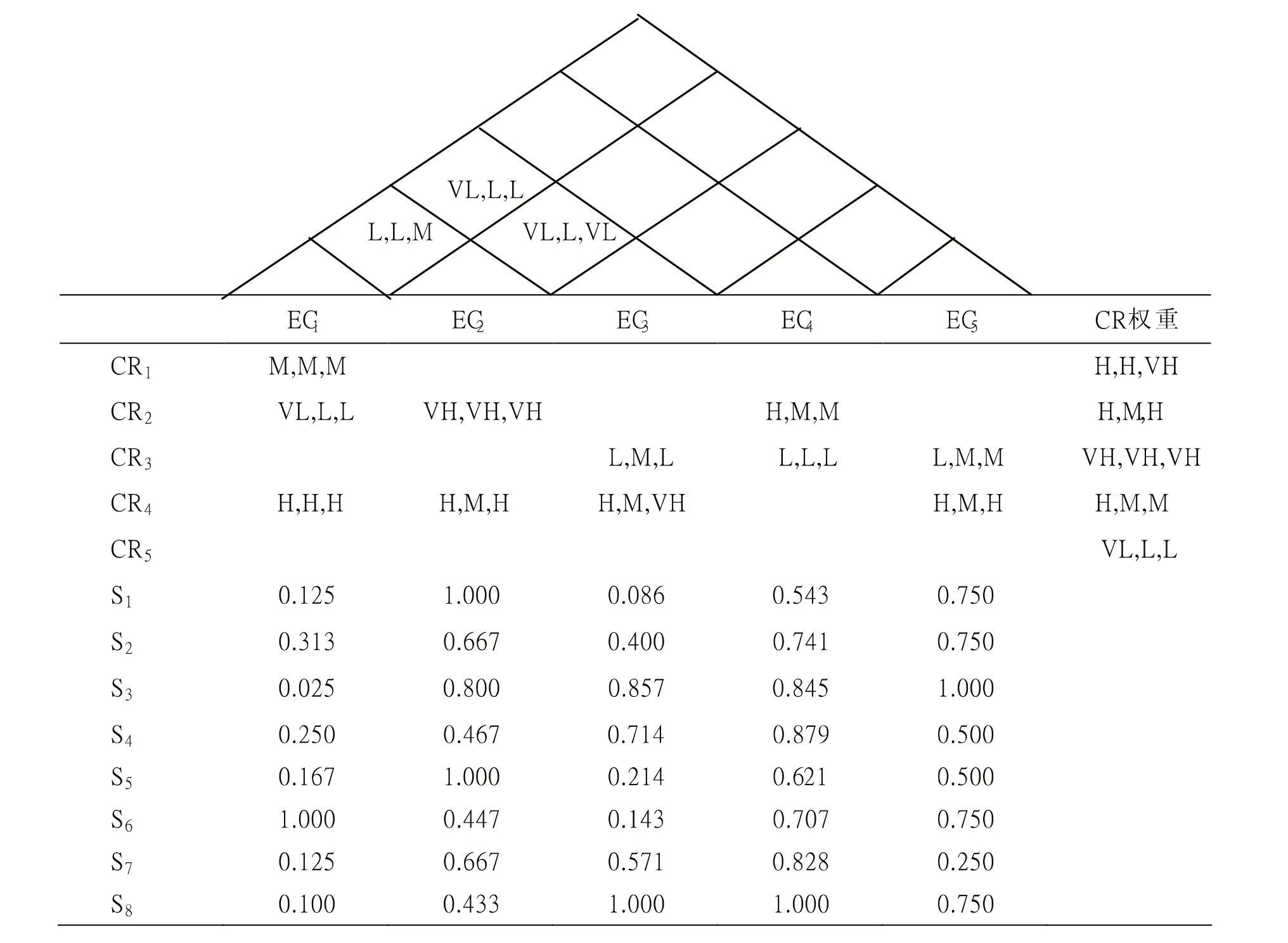
图6 H公司石英砂供应商选择质量屋Fig 6 Quartz sand supplier selection HoQ of H company

H公司邀请3位专家对CR-EC关系、EC间关系和CR权重进行打分（如M，M，M），图中的空白处表示此处对应的元素关系可以忽略不计。利用上文中所介绍的专家权威度模糊测度方法，综合考虑各专家的相关经验和能力水平，最终确定出3位专家的权重，分别为0.2，0.5，0.3。根据公式（1），将CR-EC关系、EC间关系、CR权重进行三角模糊化，分别得到表3、表4和表5。

表3 顾客需求与工程特性的三角模糊化Tab 3 Triangular fuzzy of customer requirements and engineering characteristics

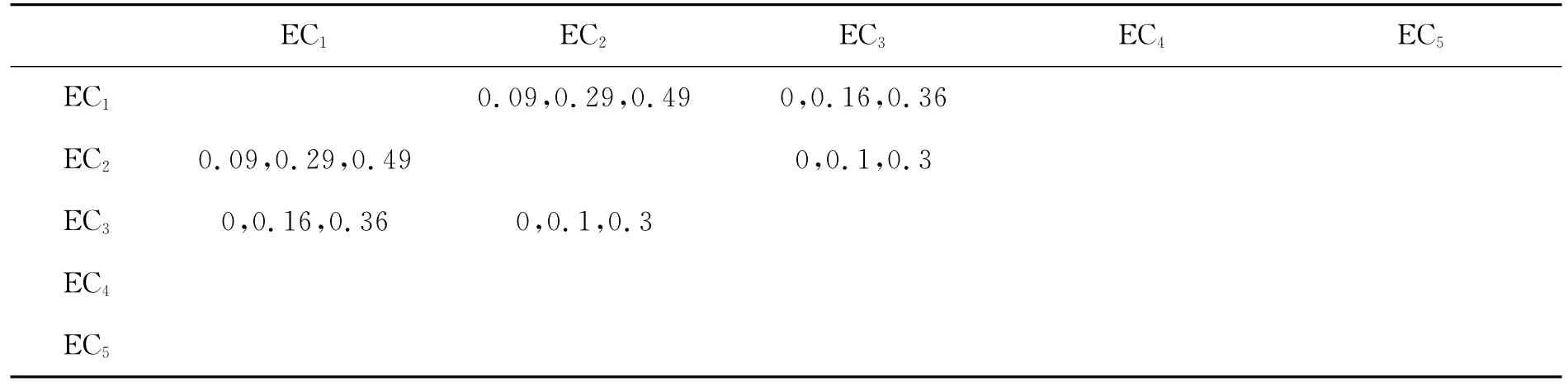
表4 工程特性自相关的三角模糊化Tab 4 Triangular fuzzy of engineering characteristics autocorrelation

表5 CR权重的三角模糊化Tab 5 Triangular fuzzy of CR weight

根据公式（3-1）和（3-2）对CR-EC关系矩阵进行标准化，考虑到数据过多，为使过程简洁化，此处省略了具体结果。然后根据（4-1）和（4-2）计算出α取不同值时EC权重的上下限，如表6所示。

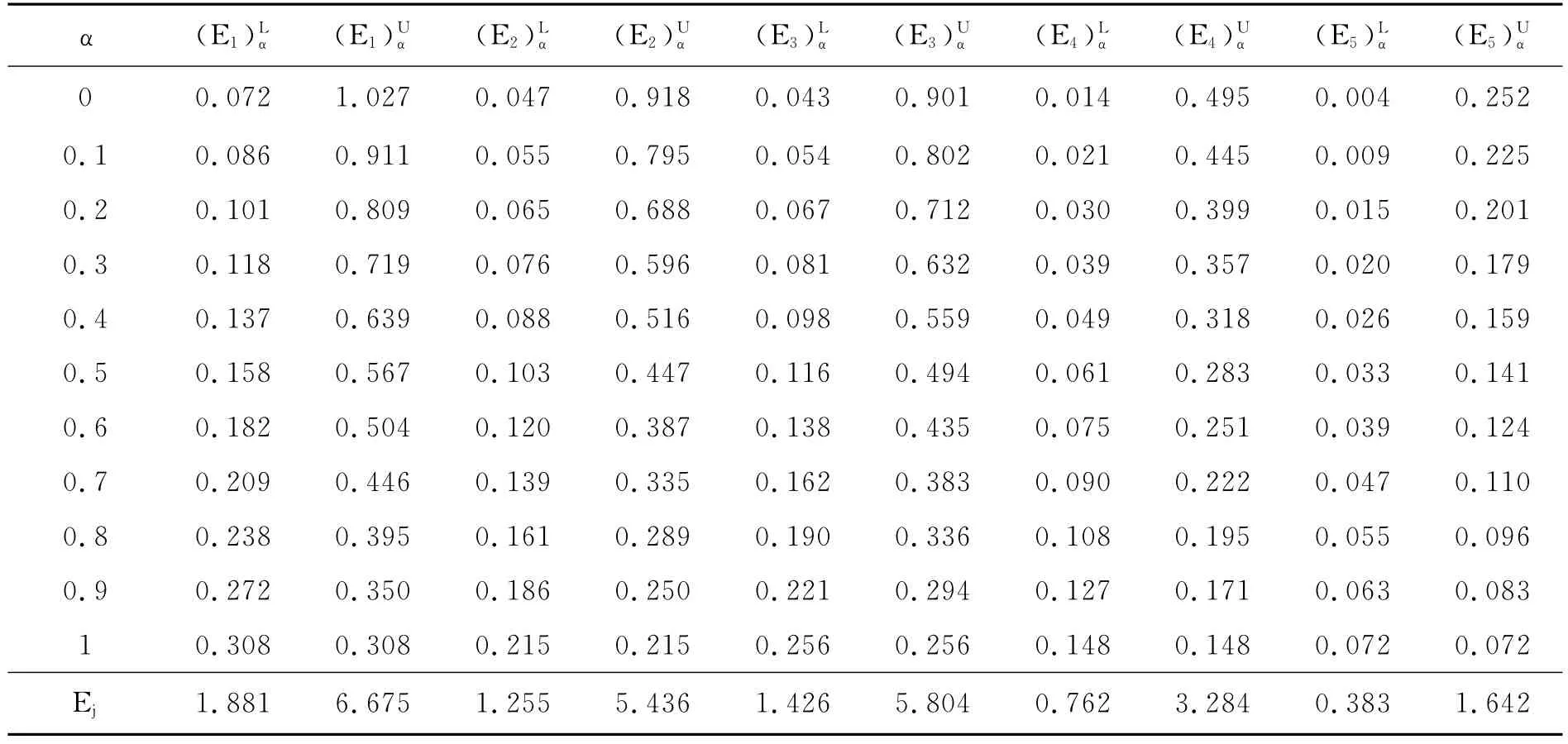
表6 不同 水平下EC权重的上限、下限Tab 6 Upper limit and lower limit of EC weights under different levels

由表5可知~E5最小，故将~E5作为参考标准项，令β＝0.5，根据式（5）计算出模糊集~E1，~E2，~E3，~E4分别到~E5的距离，依次为0.272，0.194，0.217，0.084。由此可知，5个工程特性因子重要度由大到小依次为：

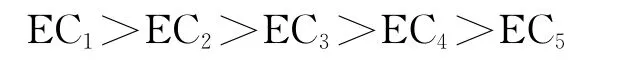
引入Kano模型，最终确定EC1为魅力型需求，EC3和EC2为期望型需求，EC4和EC5为基本型需求。根据参考文献［12］，现设定Kano系数为：Q1＝2，Q2＝1，Q3＝0.5。

根据公式（6）可计算出8个石英砂供应商的最终总得分，为保证决策的中立性，令α＝μ＝0.5，如表7所示。

由表可知，各石英砂供应商的得分由大到小依次为：

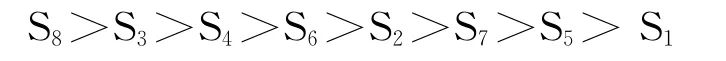
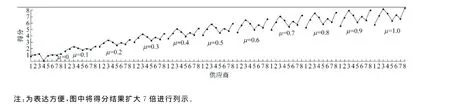
图7 供应商排序结果Fig 7 Result of supplier sorting

在本文所建的模型中，决策系数α和μ的取值均对排序结果产生影响，通常取0.5，而μ由决策者决定，易受决策者偏好的影响，因此，为证实本文所用方法对μ的鲁棒性，现对决策结果进行敏感性分析。

表7 各供应商的总得分和排序结果Tab 7 Total scoring and sorting results of each supplier

令μ分别取0，0.1，0.2，…，1，根据公式（6）计算各供应商总得分，排序结果如图7。

从图4中可以看出，除μ取0时的排序有所不同，其他10段折线的走势基本一致，也就是说，供应商的排序结果并不受μ的取值的影响，故该公司选取的基于质量功能展开和Kano模型的模糊供应商选择方法体系具有很好的鲁棒性。

综上可知，成都茂岩矿业有限公司（S8）在河南省中联玻璃有限责任公司的所有备选石英砂供应商中具有显著的竞争优势，英德信和祥石英砂厂（S3）和北海市福来成石英砂有限责任公司（S4）稍次之，H公司决策者在结合某些客观因素和突发状况进行综合考虑之后，最终选择S8和S4为其主要石英砂供应商，S3为后备应急供应商。

结 语

任何企业都不可能独立于行业环境而自行运转，供应链便是通过节点企业的纵向与横向合作而集结成一体的，因此，为保证企业的正常运作，各企业势必需要与其他企业建立合作伙伴关系，而如何选择适合本企业发展的合作伙伴就显得至关重要。［13］

供应链管理的精髓和最显著特征就是建立企业间的合作关系，国内外一些实力强大的制造商，如 Nestle（雀巢）、General Motors（通用汽车），和一些掌握统治权的零售商，如Carrefour（家乐福）、沃尔玛，以及一些资金雄厚的批发商都在极力促进与供应链其他成员的合作，实现物流、信息流、资金流三流的融合，使各方企业均收益。

而且，各节点企业都应该认识到，合作伙伴关系的建立并不是一劳永逸的事情，无论是外界社会环境还是企业内部运作环境都是复杂而多变的，企业很可能受到利益的驱使而背弃当初的合作协议，因此，企业应该不断跟进对合作伙伴关系的维护和完善。

然而，目前供应链节点企业间合作问题的研究还处在初级阶段，相关理论体系还很不完善，还有很大的发展空间。随着信息技术的推广和可持续发展思想的深化，供应链管理的全球化、信息化、绿色化将成为研究领域的热点，而这也终将促进供应链合作伙伴选择相关研究领域的蓬勃发展。

［1］Charles C.Poirier，Francis J.Quinn.How are We Going？A Survey of Supply Chain Progress［J］.Supply Chain Review，2004，11（2）：69-73.

［2］王道平，李淼.供应链设计理论与方法［M］.北京：北京大学出版社，2012.

［3］史腾欢，吴和成.基于Fuzzy-QFD的物流供应商选择方法研究［J］.江苏师范大学学报（自然科学版），2013，31（4）：26-31.

［4］晁梦娜，王玫.基于QFD-灰色关联度模型的ERP供应商选择研究［J］.北方经济，2015（1）：40-42.

［5］杨敏敏，付瑞.基于QFD方法的敏捷供应链设计［J］.青岛大学学报：工程技术版，2014，29（4）：99-105.

［6］Chen Liang-Hsuan，Weng Ming-Chu.A fuzzy model for exploiting quality function deployment［J］.Mathematical and Computer Modeling，2003，38（7）：559-570.

［7］孙园园，刘飞，李丽.基于Kano-QFD的个性化产品属性指标重要度确定方法［J］.计算机集成制造系统，2014，20（11）：2697-2703.

［8］Chen Liang-Hsuan，Lu Hai-Wen.An Approximate Approach for Ranking Fuzzy Numbers Based on Left and Right Dominance［J］.Computers and Mathematics with Applications，2001，41（3）：1589-1602.

［9］金刚，李明.基于质量功能配置的客户需求分析研究［J］.制造技术与机床，2009（8）：116-126.

［10］Karsak E.Fuzzy multiple objective programming framework to prioritize design requirements in quality function deployment［J］.Computers＆Industrial Engineering，2004，47（8）：149-163.

［11］王霜，殷国富，何忠秀.基于Kano模型的用户需求指标体系研究［J］.包装工程，2006，27（4）：209-213.

［12］蒋秀军.整合Kano模型与QFD的物流服务设计方法及应用［D］.江苏：江苏科技大学，2012.

［13］程拱胜，尹宏.物流服务供应链研究现状探析［J］.中国商贸，2010（11）：149-150.