基于曲波变换的面波去噪方法研究
2015-12-03姚恒星谢凯长江大学电子信息学院湖北荆州434023
姚恒星,谢凯 (长江大学电子信息学院,湖北 荆州434023)
在地震勘探领域中,噪声严重影响了地震资料的后续处理,因此如何有效地提高地震资料信噪比是地震资料处理的首要任务。面波[1]作为一种常见的规则干扰,在叠前数据上呈扫帚形状,具有低频能量强等特点,严重影响了地震有效反射波,而且还降低了地震数据的信噪比。常见的去除面波的方法有低通或高通滤波、F-K频率波数谱滤波[2]等。每种方法有着一定的效果,但这些方法都只侧重考虑了面波单一的特性,有着较大的局限性。二维小波变换去噪[3]虽然可以压制噪声,但它是以点为元素来描述信号图像特征,无法有效地表达边缘信息,并且还会损伤有效信号。为此Candès等提出了曲波变换[4,5](Curvelet),即基于脊波变换的多尺度多分辨率的几何分析方法[6]。该变换称为后小波变换,不仅弥补了小波变换的不足,还可以更加有效的表示二维图像,具有各向异性、方向性和局部性,可以稀疏表达图像的平滑区域和边缘区域[7,8]。把地震数据看成是二维图像,可以利用面波的方向性[9,10],用曲波变换去噪的方法去除面波的同时能够有效地保护有效反射信号。为此,笔者提出基于曲波变换的面波去噪方法研究。
1 曲波变换的基本原理
第1代曲波变换的数字实现很复杂,需要子带分解、正规化、平滑分块和脊波分析等许多步骤,并且在进行曲波金字塔分解时带来了巨大的数据冗余。因此,Strack等在第1代曲波变换的基础上提出了第2代曲波变换的新框架体系。第2代曲波变换在构造上已经完全不同于第1代曲波变换,实现过程不需要用到脊波变换,直接通过构造曲波窗函数来实现曲波分解,不仅变换意义明确,而且实现起来更加快速和方便。
曲波变换和小波变换属于稀疏理论的范畴,都是利用基函数与信号作内积来实现信号的稀疏表示。曲波变换可表示为:

式中,φj,l,k表示曲波函数,j,l,k分别表示尺度方向和位置参数。
下面介绍第2代曲波变换的基本原理。曲波变换在频域内的实现是采用频域中的窗函数来表示的,首先构造径向窗和角度窗W(r),r∈和V(t),t∈[-1,1],那么对所有尺度j,傅里叶频率窗Uj定义为:

式中,[]表示的整数部分;Uj是受W和V支撑区间的限制而获得的楔形区域,如图1所示的阴影区域。
定义在尺度j,方向θl,位置参数k=(k1,k2)处的连续曲波变换为:

式中,(ω)是二维有效信号的频域表示表示对φj,l,k(ω)取共轭;Rθl由θl旋转获得;=·2-j,k2·2-j2)。
和小波基础理论一样,曲波变换包括粗尺度和精细尺度。粗尺度的曲波变换不具有方向性,所以整个曲波变换是由粗尺度下各向同性的小波和精细尺度下的方向元素组成的。
把笛卡尔坐标系下的二维函数f(t)作为有效信号,离散曲波变换定义:

式中,cD(j,l,k)是曲波变换系数的离散形式(t)是曲波函数的离散形式。
第2代曲波变换的快速算法有2种:USFFT算法和Wrapping算法。笔者采用基于Wrapping的快速离散曲波算法,其核心思想是围绕原点Wrapping,对任意区域周期化,再一一映射到原点仿射区域。过程如下:
1)对给定的二维函数f[t1,t2]进行二维 FFT,得到频域表示[n1,n2],-≤n1,n2≤。
2)在频域,对每个尺度和角度组(j,l),重采样[n1,n2]得到[n1,n2-n1tanθl],(n1,n2)∈Pj。
3)内插后的与窗函数相乘得到[n1,n2]=[n1,n2-n1tanθl]^Uj[n1,n2]。
4)围绕原点 Wrapping局部化[n1,n2]。
5)对,l进行二维IFFT(FFT的逆变换)得到离散曲波系数集合CD(j,l,k)。
Wrapping算法基本思路如下:首先变换到频域,再在频域中局部化,最后采用二维IFFT得到曲波系数。此外局部化和二维IFFT可合二为一,即用局部化窗口来乘局部傅里叶基。该算法采用3个参数,使得理解更容易,运算操作更简便,冗余度更低。

图1 曲波变换的时域和频域
2 面波去噪方法
对于地震数据的噪声去除问题,通常采用的方法是通过变换将信号去噪问题从时域转换到频域加以解决。基于曲波变换的面波去噪方法如下:首先对经过预处理的含噪信号进行多尺度分解,然后在各尺度下尽可能提取出有效信号的曲波系数,同时去除噪声的曲波系数,最后用曲波逆变换重构出地震信号,从而达到去噪目的。
设地震信号为s,有效信号为d,噪声为n,则含噪声地震数据可表示为:

有效信号可用下述方法估算,即:

式中,C表示曲波变换;C-1表示曲波逆变换;Cs表示对地震信号s作曲波变换后的系数;F表示阈值函数,定义为:

式中,m为大小与尺度有关的常数;σc为曲波域中噪声标准差;σ为噪声标准差。
该方法所述的地震信号去除面波方法的流程包括4个步骤:
1)通过对大量含面波的实际叠前地震资料进行分析,确定地震信号中包含的噪声模型及其相应的各项参数,从许多具有代表性的面波里取其平均作为面波噪声模型。
2)因为地震信号是二维的,在空间域中分析存在很多局限性。由于曲波变换具有多尺度和多方向性的特点,能够稀疏地表示二维信号,使得在曲波域中能更精细地分离出面波噪声和有用地震地震反射信号。该方法对二维地震数据进行曲波分解,选择合适的尺度,将空域地震信号变换到曲波域中,得到地震信号的各方向各尺度的曲波系数。同时对面波模型也进行曲波分解,得到面波曲波系数,将面波数据变换到曲波域。
3)根据面波噪声模型的曲波系数在不同尺度和方向上的分布特点来设置去除面波的阈值。接着采用阈值去噪法,低于阈值的系数可以认为是面波的曲波系数,从而将其置零去掉;大于阈值的系数认为是有效反射信号的曲波系数,将其保留。
4)对滤掉面波后的曲波系数进行曲波反变换,重构得到去噪后的地震信号。
3 试验结果与分析
笔者分别对合成地震资料和叠后实际资料进行了相应处理。其测试结果如图2所示。
图2(a)是理论合成数据,该模型有2条主频为35Hz和45Hz的反射同相轴和1条主频为15Hz的面波同相轴,2条斜线代表面波,2条曲线代表有效反射波。该模型数据由100道组成,每道包括600个采样点。图2(b)是采用笔者所描述的方法去噪后结果,图2(c)是去除掉的面波。由图2(c)可见去除的大部分是面波。

图2 模型地震数据的去噪结果对比
图3(a)是含面波实际地震数据,共33道,每道1501个采样点。从图3(a)中可以看出,原始实际地震数据受面波干扰严重,许多有效波同相轴无法识别。笔者设计了包含面波的噪声模型,将地震数据和面波噪声模型都进行曲波分解,得到其在曲波域中的表示。根据面波噪声模型在曲波域中分布的尺度和方向,确定了滤波阈值,然后根据此阈值对地震信号的曲波系数进行处理。图3(b)是滤波后的重构图像显示效果,可以看出有效波的水平同相轴变得更加清晰,部分在处理前无法识别的反射层在处理后显现出来。图3(c)是通过该方法处理所去除掉的面波噪声。
表1是实际地震数据去除面波前后的信噪比对比,抽取的是地震数据的前10道数据。由表1中可以看出在经过曲波变换去面波处理后,地震数据的信噪比有了明显的提升,由此可见曲波去面波方法具有较强的实用性。
4 结语
通过以上试验可知,将该方法运用于地震信号的去噪处理,能够充分利用面波在曲波域中的分布特点,有效地压制面波干扰并保护反射地震信号,重构后的地震有效反射信号同相轴变得更加清晰,不仅提高了信噪比,还提高了成像质量。

表1 实际地震数据去噪信噪比对比
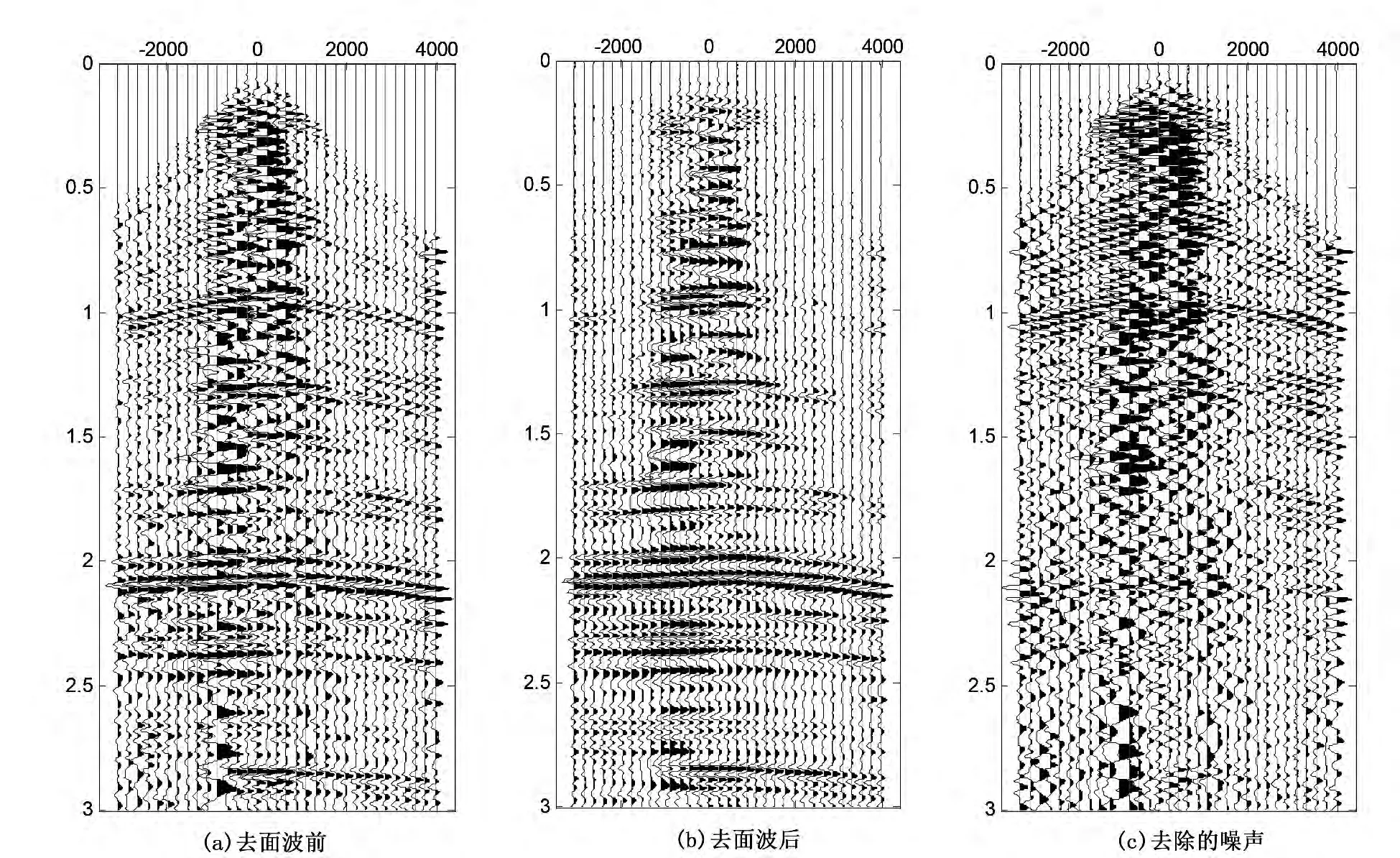
图3 实际地震数据的去噪结果对比
[1]李晶 .面波在地震波场中的特性研究及其应用 [D].成都:成都理工大学,2006.
[2]李彩芹,张华 .小波变换与F-K联合滤波在面波分离中的应用 [J].中国煤田地质,2007,19(4):60~61,84.
[3]林椹尠,宋国乡,薛文 .图像的几种小波去噪方法的比较与改进 [J].西安电子科技大学学报(自然科学版),2004,31(4):626~629.
[4]董烈乾,李振春,王德营,等 .第2代Curvelet变换压制面波方法 [J].石油地球物理勘探,2011,46(6):897~904.
[5]蔡炳煌 .基于曲波分析的图像处理与应用 [D].汕头:汕头大学,2007.
[6]才溪 .多尺度图像融合理论与方法 [M].北京:电子工业出版社,2014.
[7]Starck J L,Candes E,Donoho D L.The Curvelet Transform for Image Denoising [J].IEEE Transactions on Image Processing,2002,11(6):670~684.
[8]Kristof De Meersman.Ground Roll polarization filtering with spatial smoothness constraints [J].SEG Technical Program Expanded Abstracts,2008(27):413~416.
[9]代虎 .地震面波资料处理的基本方法 [J].黑龙江水利科技,2012,41(9):28~30.
[10]张恒磊,刘天佑.Curvelet域蒙特卡罗估计的噪声衰减 [J].西南石油大学学报(自然科学版),2011,33(4):64~68.
