尼尔森选矿机离心锥的有限元分析研究

刘祚时

（江西理工大学 机电工程学院，江西 赣州 341000）

尼尔森选矿机离心锥的有限元分析研究

刘祚时

（江西理工大学 机电工程学院，江西 赣州 341000）

尼尔森选矿机是分选回收目标矿物的一种新型高效离心重选设备，其分选的关键在于离心锥。研究应用有限元方法对离心锥的结构进行静力学和动力学特性分析，采用ANSYS软件完成计算。计算结果表明，工况下内锥的应力分布比较均匀，最大变形出现在分选部分，离心锥的静力结构满足强度和刚度要求，但也存在比较薄弱的部分。随着离心锥频率的增大，其主要变形由大端逐渐转移到中间部分，且内锥的变形比较剧烈，但尼尔森选矿机的设定转速小于各阶临界转速，因此离心锥的结构动力学特性基本满足要求。对尼尔森选矿机离心锥的有限元分析结果可以为设备的设计和改进提供借鉴。

尼尔森选矿机；离心锥；有限元；结构分析；模态分析

0 引言

随着矿产资源的不断开采利用，富矿和易选矿日趋减少，可利用的资源主要以复杂、贫细、难处理矿居多[1]。近年来，应用离心力场提高颗粒沉降速度的原理来改善微细颗粒的回收成为国内外研究的热点,其中尼尔森立式离心选矿机因其对微细粒矿有较高的分选效率引起科研人员的兴趣。采用离心分选技术不仅可以减少有用微细颗粒的流失，而且降低了“尾矿”和“废石”对环境的危害[2]。

尼尔森选矿机适用的选矿工艺有[3-4]：磨矿回路中回收目的矿；尾矿中回收目的矿；半连续式选矿机适用于目的矿含量很低的贵金属矿回收，如岩（脉）金、砂金及有色金属伴生金的回收等；连续式选矿机主要用于黑（白）钨矿、锡石、铁矿和含金银的硫化物等较大比重矿物的富集，以及从尾矿中回收含金的硫化物，进行工业矿物的除铁等。

虽然立式离心分选技术应用方面发展较快，但由于离心分选过程的多样性和复杂性，设备内部结构直接影响矿浆的运动规律。目前其他类型的立式离心选矿机（如法尔肯选矿机、超转筒式离心选矿机等）都是在尼尔森选矿机的结构或分选原理的基础上研制的新机型。大家围绕尼尔森选矿机开展了许多研究工作，麦吉尔大学M．Greenwood等[5]利用尼尔森选矿机进行了钨矿干选和湿选工艺的对比试验，证明了尼尔森选矿机的干选潜力；哥伦比亚国立大学Luis A．Meza等[6]通过尼尔森选金试验说明反冲水压力的取值范围；清华大学温雪峰等[7]建立了在法尔肯选矿机分层区和分选区中球形颗粒的动力学方程，验证了实现微细颗粒快速沉降的关键因素是离心加速度。

尼尔森选矿机对密度较大的金属矿分选效果好，但分选部件的离心锥设计目前还主要依靠经验。随着计算力学和CAE技术的发展，应用有限元技术研究离心锥的力学特性，为设备的结构设计优化和提高设备分选效率，促进矿产资源的高效利用具有重要的意义。

1 离心锥结构分析

1.1 离心锥作用

尼尔森选矿机由分选部件（即离心锥）、支撑部件、给矿排矿装置、驱动装置、传动装置、供水（气）装置以及自动控制系统等组成。整台设备由电机驱动，通过带轮传动使联接在中空主轴上起分选作用的部

件离心锥以一定的角速度匀速旋转，工作时，矿浆由给矿槽进入锥体，在离心力场中沿锥壁作旋转流动，运行状态下，离心锥内可以产生离心加速度为60～180 G的离心力场[8]，矿浆在高速旋转的离心锥内沿着锥壁流动，形成一种特殊的分选床层——流化床，通过作用在矿粒上离心力的差异，反冲水的流态化松散作用，矿粒在流化床中运动、沉降，最后实现分选。

1.2 离心锥的结构

尼尔森选矿机离心锥的结构经历了多次改进[9]。现阶段的结构特点为：由两个同轴的锥套构成；环形格条设计为楔形结构；内锥用聚氨酯铸造，其结构简图如图1，这种设计制造方便，使用寿命长，能够获得较好的流态化和更高的富集比。

图1 离心锥结构Fig.1 Structure of centrifugal cone

2 离心锥的有限元分析

有限元法在数值模拟中可不受计算对象几何形状限制，便于分析复杂造型的结构设备，从而广泛应用于产品的结构设计中，为结构的合理优化提供了可靠的依据[10]。在对离心锥的有限元分析中，为体现结构的一般性特点，选择KC-CD12型尼尔森离心选矿机为分析对象，以ANSYS有限元分析软件为主要技术手段，对离心锥进行分析计算。

2.1 结构参数

尼尔森选矿机的离心锥由内锥和外锥等零件联接。内外锥不发生相对运动，二者主要的结构参数如表1及图2所示。

表1 内锥和外锥结构参数Tab.1 Structure parameters of inner cone and outer cone

内锥的环形沟槽内壁都有两圈相间排列的反冲水孔，为避免微细颗粒从水孔流入水腔，同时，防止过量的反冲压力水造成精矿颗粒的流失，设计小孔的直径为1 mm，共计606个。内锥分为上下两锥段，上锥段是分选锥部分，下锥段用于在停机冲洗过程中，通过倾斜的锥段使精矿颗粒顺利进入精矿槽。下锥段部分设置导流板，目的是使矿浆均匀流向分选锥部分和消减矿浆的冲击磨损。为提高运算速度，在不影响计算结果精度的前提下将离心锥中部分微小结构作适当简化，省略锥鼓开孔的具体结构影响，将其质量转化为壁厚，保持内锥的整体质量和质心不变。

图2 尼尔森选矿机离心锥内锥和外锥结构Fig.2 Inner and outer structures of centrifugal cone

2.2 离心锥有限元模型

利用实体造型软件Pro/ENGINEER建立模型，然后通过导入ANSYS软件进行分析处理。为了减少单元数量和提高网格质量，在建立有限元模型时需要进行多方面的合理简化[11]。由于ANSYS软件在处理圆角和倒角时需要大量的单元，因此计算模型对一些非应力集中或非重点分析的地方进行了简化，忽略了圆角和倒角等局部特征，以提高运算效率。

导入ANSYS的内锥模型，采用以六面体主导的网格划分方法（Hex Dominant），单元尺寸为5 mm，划分后节点数为113357，单元总数为33595；外锥模型采用同样的方式划分，划分后网格节点数为94437，单元总数为19 300；离心锥的有限元模型如图3。内锥材料为聚氨酯PU，外锥材料为奥氏体型不锈钢1Cr18Ni9Ti，材料的物理性能见表2。

表2 材料性能参数[12-13]Tab.2 Material performance parameters

图3 离心锥网格Fig.3 Centrifugal cone grid

2.3 载荷与约束条件

对有限元模型添加零位移约束、转动惯量和相应的工况载荷，然后求解该工况下的应力应变。对离心锥工况下的载荷与边界条件分析如下：

（1）离心锥垂直固定在主轴上并同步旋转，则通过零位移约束限制其自由度；（2）离心锥的转速为600 r/min，计算其角速度为62．8 rad/s，即离心锥的转动惯量；（3）当选矿机转速大于290 r/min时，流膜厚度基本保持一个固定值[9]，一般为1～2 mm，不妨取b=1．8 mm，矿浆的密度取ρ=2 400 kg/m3。根据公式Pc=ρω2（R2-r12）/2可得内锥所受载荷。为简化分析，锥壁各位置处液压取该液层的平均值。计算所得工况下压力载荷：槽内壁由下至上10．76 kPa、11．38 kPa、11．96 kPa、12．4 kPa、13．06 kPa、14．09 kPa，环壁面由下至上1．72kPa、1．87kPa、1．96kPa、2．06kPa、2．16kPa、 2．25 kPa、2．34 kPa；（4）反冲水压根据颗粒类别、颗粒大小等因素确定，一般设定为0．02 MPa[9]。于是，内锥外壁和外锥内壁所受的压力载荷是20 kPa。根据以上分析，在有限元模型上分别设置内、外锥以及二者组合件所受的约束与载荷。

2.4 结构分析结果

假设给矿速率、给矿浓度、反冲水流量和离心锥转速等工艺参数没有受外界干扰，不发生变化。离心锥安全运行的前提是保证结构在工况下满足强度和刚度的要求，由于内外锥的材料不同，现分别进行结构分析。

（1）内锥的应力和变形。图4为内锥应力云图。由图4可见，工况下内锥的应力分布比较均匀，最大应力出现在下端边缘处，最大值为10．4 MPa（综合应力）。经比较分析，在空载下内锥的应力由下端向上端递增，且最大应力出现在上端，其值约为0．12MPa。由于聚氨酯的许用应力为26 MPa，考虑其安全性，取安全系数ns=2，开孔削弱系数φ=0．83。则σn=10．4 MPa≤[σs/ns]·φ=10．8 MPa，即内锥设计强度满足在工况下的要求，但应考虑下端的支撑部分。

图4 内锥应力云图Fig.4 Stress nephogram of inner cone

图5 内锥变形云图Fig.5 Deformation nephogram of inner cone

由内锥变形云图（图5）可见，工况下内锥的最大变形出现在分选部分，最大值为0．385 mm（综合变形），不会产生干涉现象。分选部分比较薄弱，容易造成刚度不足，给矿时应限制进矿量和转速等因素。

（2）外锥的应力和变形。外锥应力云图和变形云图见图6、图7。由图6可见，外锥的应力分布均匀，下端平面的应力较上端环边的应力大，底端排矿孔边缘产生最大应力，最大应力为124 MPa（综合应力）。这是因为下端平面承受较大的载荷造成的。由于不锈钢的屈服强度为215MPa，强度极限为520MPa，从经济性方面考虑，取安全系数ns=1.5，nb=3.5。显然，σn=124 MPa≤[σ]=min[σs/ns，σb/nb]=143.3 MPa，即外锥设计强度满足要求。

由图7可见，外锥的上端出现较大变形，底端平面的变形由外向内递减，变形的最大值为0.147mm（综合变形），不会产生干涉现象。

图6 外锥应力云图Fig.6 Stress nephogram of outer cone

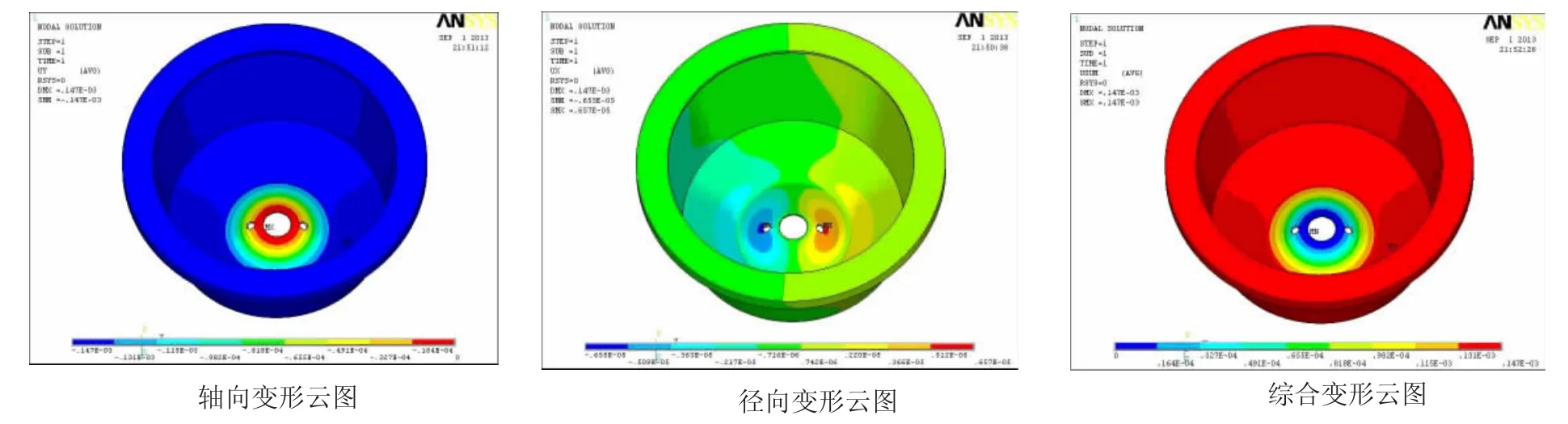
图7 外锥变形云图Fig.7 Deformation nephogram of outer cone

（3）离心锥的综合变形和综合应力。有限元结构分析结果表明，离心锥最大变形量为0.070 3 mm，位于内锥的下部，变形由下至上不断变小；最大应力值为23.4 MPa，位于离心锥底部（见图8、图9）。将这一结果与相应的材料性能进行比较，说明离心锥的静力结构能满足强度和刚度要求，但也存在比较薄弱的部分。所以，应该合理控制设备的转速，避免结构疲劳破坏。

图8 离心锥综合变形云图Fig.8 Integrated deformation nephogram of centrifugal cone

3.1 动力学特性分析的理论计算

动力学特性是指系统的模态特性和在模态特性基础上的各类响应，主要体现为系统的固有频率和振型。对回转系统而言，还包括转动系统的临界转速。离心锥高速旋转，极易出现振动和动不平衡现象，因此应对其进行模态分析，防止设备的工作转速接近或等于系统的固有频率而引起共振，造成损坏。

图9 离心锥综合应力云图Fig.9 Comprehensive stress nephogram of centrifugal cone

3 离心锥的固有频率计算

假设初始激励为零，即F（t）=0，忽略阻尼影响，其无阻尼模态分析通用方程的形式为：

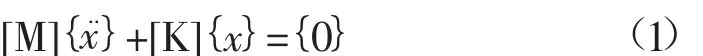
式中：[K]和[M]都为常量。

若结构的自由振动为简谐振动，则位移为正弦函数，即：

代入式（1）得：

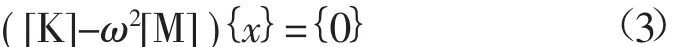
式中：ω为自振圆频率，若方程的特征值为ωi，则自振频率为f=ωi/2π，而特征值对应的特征向量｛xi｝为自振圆频率下的振型。

2.2 分析结果与临界转速

通过ANSYS有限元分析软件完成离心锥安装定位后的模态分析，求解阶数选择10阶，分别进行空载状态下和工况下的模态分析。

自由状态固有频率用于约束低转速运动，预载状态固有频率用于限制高转速运动。KC-CD12尼尔森离心选矿机的转速为600r/min，换算成频率为10Hz，而计算结果表明，自由状态固有频率的最低值为37．327 Hz，最高值为777．20 Hz，于是，选矿机的工作转速不在离心锥固有频率范围内，不会引起共振。

通过ANSYS分析软件模拟离心锥在自由状态时的前八阶振型，如图10所示。

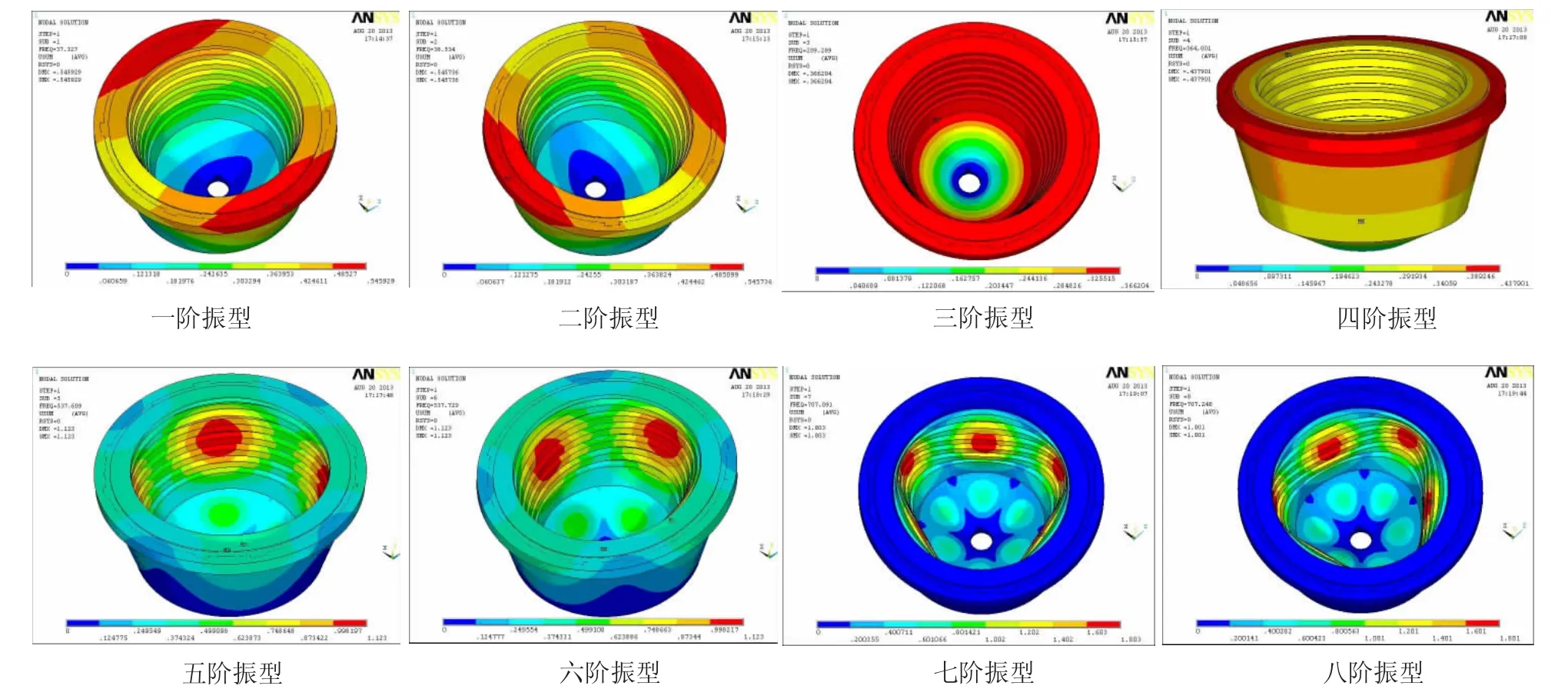
图10 离心锥自由状态前八阶振型Fig.10 Vibration mode of the first eight order for the centrifugal cone in its free state

从振型来看，随着离心锥频率的增大，其主要变形由大端逐渐转移到中间部分，且内锥的变形比较剧烈。通过预应力加载后，离心锥的固有频率有所提高。因此，理论上，尼尔森选矿机在工作转速下，不会发生共振，但实际工作中，因加工制造误差、材料性质和矿浆的不均匀性等因素的存在，还是会产生振动。

经计算，固有频率对应的临界转速如表3。由表3可见，尼尔森选矿机的设定转速小于各阶临界转速，因此，离心锥的结构动力学特性基本满足要求。

表3 离心锥的临界转速Tab.3 Critical speed of the centrifugal cone

4 结语

利用ANSYS建立相应的有限元模型，完成了尼尔森选矿机离心锥的静力学与动力学特性研究，完成了系统的模态分析，得到了系统在自由状态下的固有频率和各阶振型，计算了相应的临界转速，验证了设定的工作转速是否合理；通过完成的离心锥结构强度和刚度的校核与应力应变分析，找出离心锥的薄弱环节，对尼尔森选矿机的设计和改进有一定指导意义。

[1] 刘惠中．重选设备在我国金属矿选矿中的应用进展及展望[J]．有色金属：选矿部分，2011，（s1）：18-23．

LIU Hui-zhong．Application progresses and prospects of gravity concentratorsin Chinese metalmine processing plants[J]．

Nonferrous Metals：Mineral Processing Section，2011，（s1）：18-23．

[2] 刘祚时，王 纯．立式离心选矿机分选锥流化床动力学分析计算[J]．矿山机械，2013，41（10）：79-8．

LIU Zuo-shi，WANG Chun．Dynamics analysis and calculation of fluidized bed in separating cone of vertical centrifugal concentrator [J]．Mining&Processing Equipment，2013，41（10）：79-8．

[3] 刘汉钊，石仑雷．尼尔森选矿机及其在我国应用的前景[J]．国外金属矿选矿，2008，（7）：8-12．

Liu Han-zhao，Shi Lun-lei．Nelson concentrator and its application prospectinchina[J]．MetallicOreDressingAbroad，2008，（7）：8-12．

[4] 谢永福，蒋志远，黄子令．尼尔森选矿机在金铜低品位大型矿山的应用[J]．矿山机械，2011，39（8）：90-92．

Xie Yong-fu，Jiang Zhi-yuan，Huang Zi-ling．Application of Nelson concentrator in low grade large mine with gold and copper[J]．Mining Equipment，2011，39（8）：90-92．

[5]GREENWOOD M，LANGLOIS R，WATERS K E．The potential for dryprocessingusingaKnelson concentrator [J]．Minerals Engineering，2013，（45）：44-45．

[6] MEZA L A，HARTMANN W，ESCOBAR C A．Recovery of placer gold using the Knelson Concentrator[J]．Innovations in Mineral Processing，1994，（1）：339-347．

[7] 温雪峰，潘彦军，何亚群，等．Falcon选矿机的分选机理及其应用[J]．中国矿业大学学报，2006，35（3）：341-346．

WEN Xue-feng，PAN Yan-jun，HE Ya-qun．Study on separation mechanism of falcon concentrator and its application[J]．Journal of China University of Mining&Technology，2006，35（3）：341-346．

[8] 王 纯，刘祚时，李 凡．尼尔森选矿机反冲水压对精矿回收率的影响分析[J]．现代矿业，2013，29（7）：128-129．

WANG Chun，LIU Zuo-shi，LI Fan．Effect analysis of Nelson concentrator recoil pressure to concentrate recovery [J]．Modern Mining，2013，29（7）：128-129．

[9] Byron Knelson．Ron Edwards．Development and economic application of Knelson concentrators in low grade alluvial gold deposits [C]//The AusIMM Annual Conference，New Zealand，1990，（3）：123-128．

[10]张 波，盛和太．ANSYS有限元数值分析原理与工程应用[M]．北京：清华大学出版社，2005．

ZHANG Bo，SHENG He-tai．ANSYS finite element numerical analysis principle and engineering application[M]．Beijing：Tsinghua University Press，2005．

[11] 浦广益．ANSYS Workbench12基础教程与实例详解[M]．北京：中国水利水电出版社，2010．

PU Guang-yi．ANSYS Workbench12 basic tutorials and example explanation[M]．Beijing：China WaterPower Press，2010．

[12]徐培林，张淑琴．聚氨酯材料手册[M]．北京：化学工业出版社，2002．

XU Pei-lin，ZHANG Shu-qin．Polyurethane material manual[M]．Beijing：Chemical Industry Press，2002．

[13]机械设计手册编委会．机械设计手册[M]．第三版．北京：机械工业出版社，2004．

Editorial board machine design manual．The mechanical design manual[M]．Third edition．Beijing：Mechanical Industry Press，2004．

Finite Element Analysis of the Centrifugal Cone of Knelson Concentrator

LIU Zuo-shi
(College of Mechanical and Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,Jiangxi,China)

Knelson concentrator,a new type of high efficiency centrifugal gravity separation equipment,is applied to separate target minerals．The key technology of Knelson concentrator is its centrifugal cone．This paper analyzes the static and dynamic properties of centrifugal cone applying finite element analysis technology and ANSYS software．The results show that the inner cone has uniform stress distribution under working conditions,with the maximum deformation in the separation part．The static structure of centrifugal cone meets the strength and stiffness demands in spite of some fragile parts．With increasing centrifugal cone frequency,the major deformation transforms from the bigger end to the middle part accompanied by fierce deformation in the inner cone．The structural dynamic features can meet the performance demands for the set speed is smaller than the rotation rate at each stage．The finite element analysis on the Knelson Concentrator provides favorable reference for its design and improvement．

KnelsonConcentrator;centrifugalcone;finiteelement;structureanalysis;modalanalysis

TD455+．5；TD402

A

2015-01-26

刘祚时（1963-），男，江西永新人，教授，本刊编委，主要从事矿山设备及其自动化技术的研究。

10．3969/j．issn．1009-0622．2015．01．015