某球面对比测量系统误差分析模型研究

梅军建，刘勇，纪兰香，邹郧，张留记，陈应波，杨艳锋

(1.中国人民解放军96617部队，四川泸州646000;2.中国人民解放军96412部队，陕西宝鸡721006;3.四川省新材料研究中心，四川绵阳621900;4.中国人民解放军96323部队，湖南怀化418000;5.中国人民解放军96373部队，青海西宁810011;6.中国人民解放军96173部队，江西景德镇323000;7.中国人民解放军96228部队，云南弥勒652300)

0 引言

在目前机械量具测量计算过程中，通用量具(如千分尺、百分表)的测量误差一般可以按照国家相关标准中相关的不确定度评定模型给出较为精确的判读［1］，而针对特定装置，则能否建立较为精确的特定误差分析模型，直接决定着误差计算结果和产品尺寸性能的评定。某球面对比测量系统主要用于某部件球面外径检测，在使用过程中，检测人员发现该系统在测量完毕进行校准时个别百分表不能完全归零，存在一些微小差异(0～0.01 mm之间)，本文将着重探求这种差异的原因，并结合算例阐述微小差异对测量结果的评定有着怎样的影响。

1 误差模型建立

某球面对比测量系统通过与待测的工件外形相吻合的特定半圆弧状的校准装置结合构型相似的龙门测量装置进行对比测量，具体示值通过百分表在工件及校准装置上的偏移量来判读。该系统由测量装置、校准装置、基准板、基准座、百分表、平台等组成，如图1所示。

根据该球面对比测量系统的结构特点，建立误差分析模型。以O1为圆心建立直角坐标系，圆心O1表示球面测量系统的圆心，圆心O2表示校准装置的圆心，圆心O1和圆心O2之间的距离d表示球面测量系统和校准装置之间的偏移量，忽略百分表的误差［2］和校准装置的误差，建立坐标系见图2，通过微分计算［3］，可以分析该测量系统的误差变化规律。

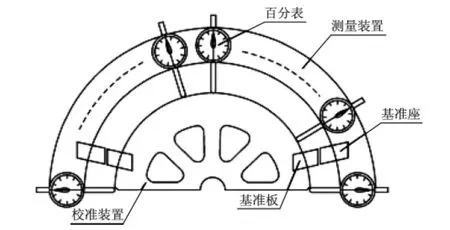
图1 球面对比测量系统

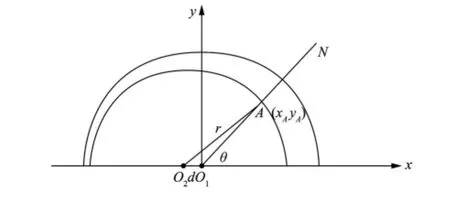
图2 球面对比测量系统数学模型

图2中，角度θ为某一百分表在该测量系统上的位置角，半径r为校准装置的标准值，直线O1N与圆心O2的交点A为百分表与校准装置的接触点，线段O1A的长度为百分表的实际偏移量测量值。

设L为测量装置与校准装置中心偏移量的最大值，根据实际情况可知0＜L＜r，因此圆O2的解析方程为

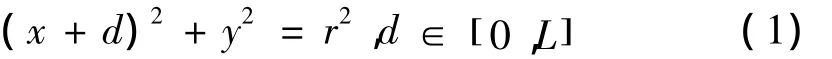
直线O1N的解析方程为

2 算例分析

对校准装置半径r以及校准装置圆心与测量系统圆心距离d分别取不同值时，由公式(10)和公式(11)计算，各角度以及算术平均误差计算结果见表1和表2。

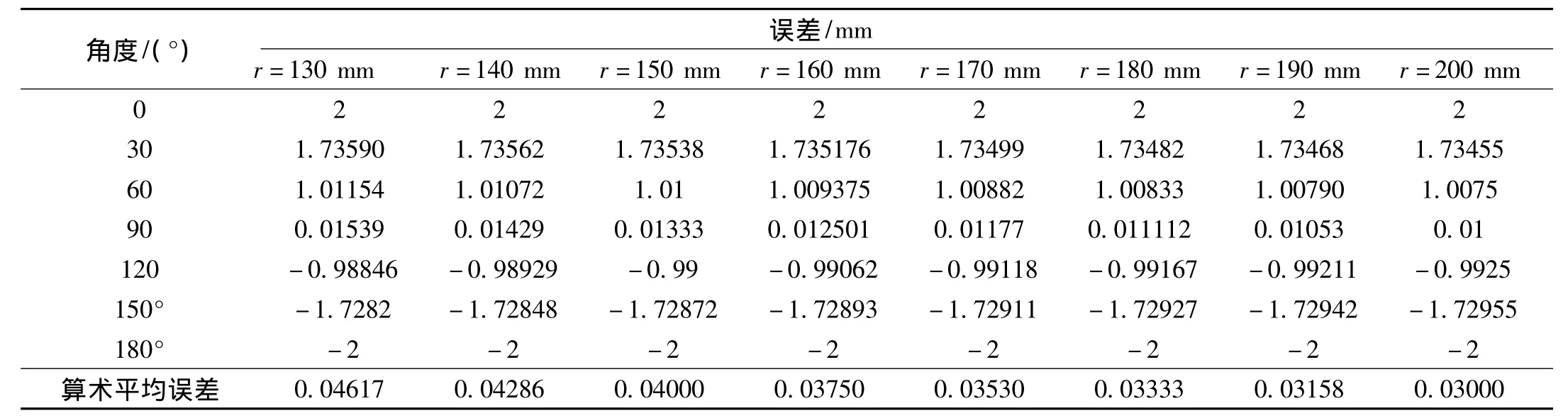
表1 校准装置半径r对误差结果的影响(d=2 mm)

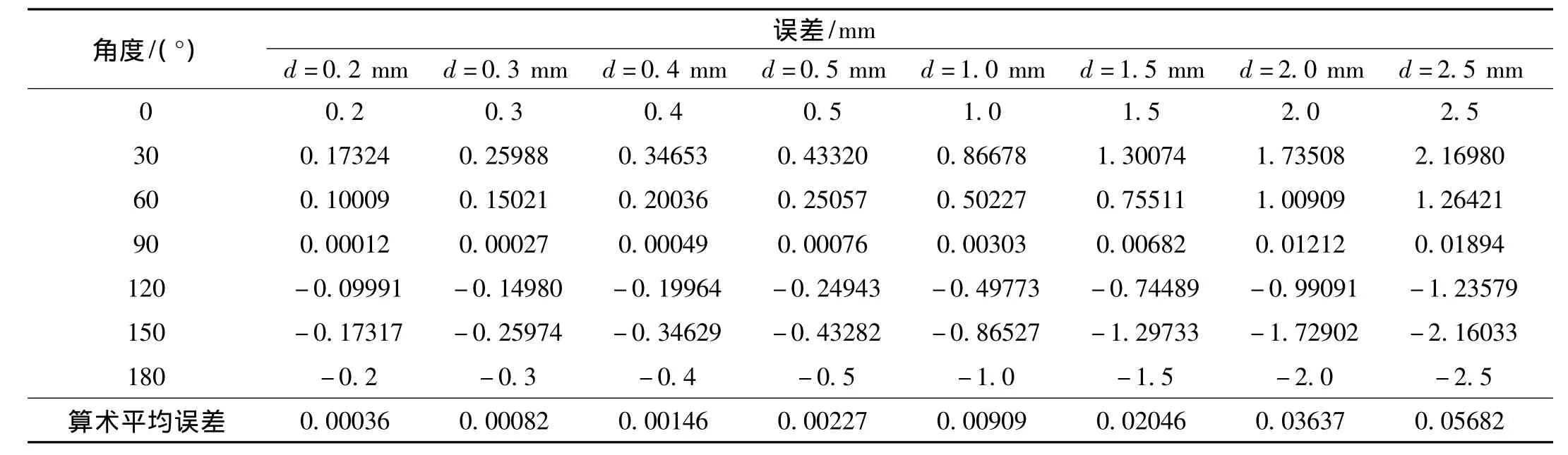
表2 圆心距d对误差结果的影响(r=165 mm)

根据表1和表2，采用折线图显示其算术平均误差随半径数和圆心距数变化规律，其变化趋势见图3、图4。

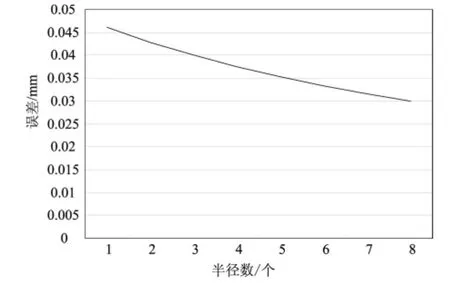
图3 误差随半径数变化趋势

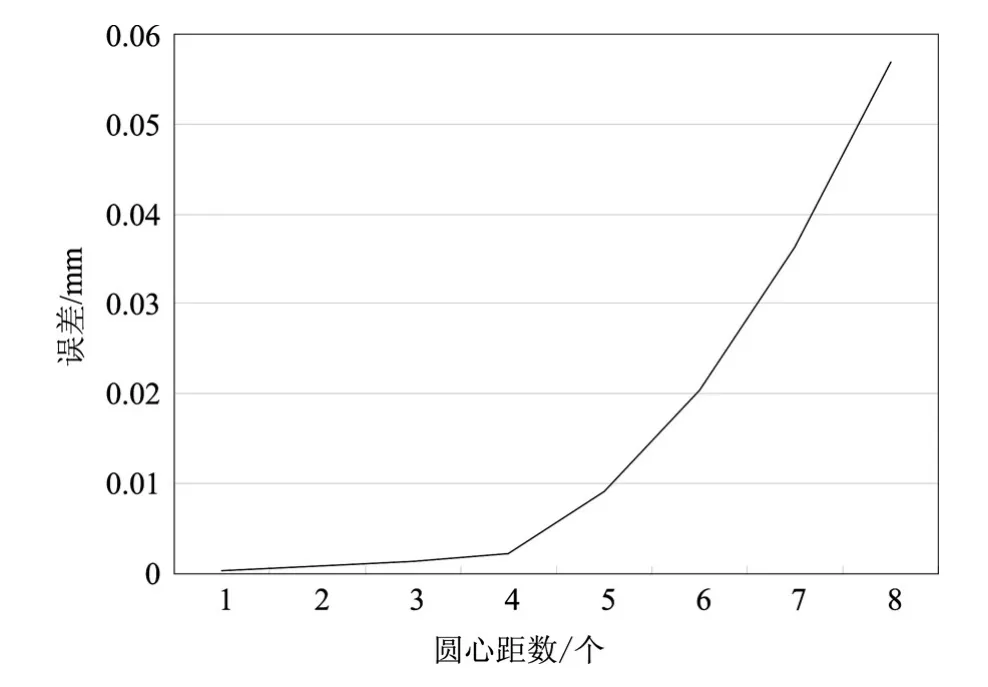
图4 误差随圆心距数变化趋势

从图3、图4可以看出，算术平均误差随着校准装置半径的增大而减小，呈现出指数分布规律，从趋势图得出其误差最大甚至超过0.045 mm，此数值只存在于理论中，实际测量过程中，校准装置半径至少都在170 mm以上，且圆心距远小于2 mm，一般最大不超过0.03 mm，且该球面测量系统的测量不确定度至少为0.03 mm。同时，算术平均误差随着圆心距d的增大而增大，且呈现出乘幂分布规律，即误差随着测量系统的基准圆心与校准装置圆心差值的增大而急剧增大。这一规律与实际情况相符。

3 实际应用

检测人员检测经过长期贮存后的某复合材料球状部件，其几何尺寸有一些微小的变化，个别尺寸即将达到临界值。采用该型球面对比测量系统进行检测，检测完毕校准时发现其百分表不能完全归零，最大偏差处0°和180°的百分表显示值为0.01 mm，各角度的误差计算结果见表3。由表3可以看出，百分表实际显示值大于计算结果。

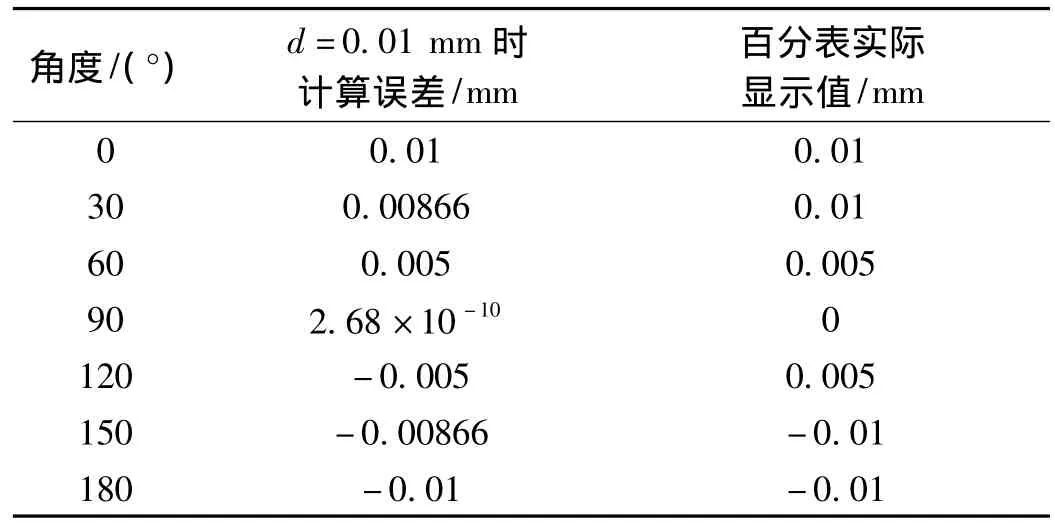
表3 各角度误差计算结果

4 结论

使用该球面对比测量系统进行检测，由于在校表过程中校表装置的放置位置导致的偏差，如果采用百分表显示值进行修正测量结果，有些角度的半径计算结果会产生较大的误差，而采用特定的误差数学模型对测量结果进行计算处理，则误差相对较小、结果更为精确。因此，在实际的测量过程中，应该对校准装置的放置位置进行精准定位，同时测量系统量程设置应该选择，由于校准装置及龙门测量装置为铸铁制造，尺寸太大太重会给人员操作带来不便，所以不适合大尺寸(半径大于700 mm)［5］的球状复合材料半径测量。通过算例的实际应用可以得出，该球面对比测量系统及误差模型可以广泛应用于中小尺寸(170～700 mm)球状复合材料的半径检测中。

［1］张成悌.测量不确定度评定中的若干问题［J］.中国测试技术，2007(9):24-27.

［2］同济大学应用数学系.高等数学［M］.北京:高等教育出版社，2010.

［3］施菊华.百分表在专用检具中的应用［J］.计量技术，2002(2):61-62.

［4］林洪桦.现代检测误差分析及数据处理［J］.计量技术，1997(1):36-39.

［5］李伟，戚晓艳.大尺寸测量的意义及发展趋势［J］.电脑编程技巧与维护，2012(8).