基于小波变换的自动化监测数据突变点识别

■赵 勇 ■上海巨一科技发展有限公司，上海 200000

现代工程在施工及运营过程中都需要进行必要的监测，比如深基坑的开挖、城市地铁线路周边施工对其影响监测、大型桥梁隧道的健康监测等等，常规的人工监测已无法满足要求，此时需要通过在关键节点上安装一定种类数量的传感器，进行实时自动化监测以保证工程施工与运营安全。实时的自动化监测必然产生海量数据，所以对数据的异常突变点识别变得比较重要。数据突变一般都说明点位包含重要信息，数据信号的突变点识别其实就是对原始数据信号进行多尺度细化，以实现高频处时间细分，低频处频率细分，最终可聚焦信号的任意细节。之前的方法应用傅立叶变换进行处理，对数据的整体突变性识别效果还可以，但对数据的局部细节识别效果稍显不足，所以基于傅立叶变换对数据突变异常点的分析还不够理想。而小波变换的时频窗自适应，可以克服这个缺点，这样我们就引入了小波变换算法。小波变换是上世纪八十年代发展的应用数学分支，它是信号的一种时频分析方法，具有多尺度分析的特点，并且在时频域皆有表现信号局部细节特征的能力，对具有的瞬态异常的原始数据处理非常适合。

1 小波变换突变点检测原理

设h(t)为函数f(t)和g(t)的卷积，即:

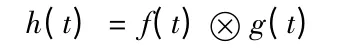
则依据傅立叶变换的特性有:

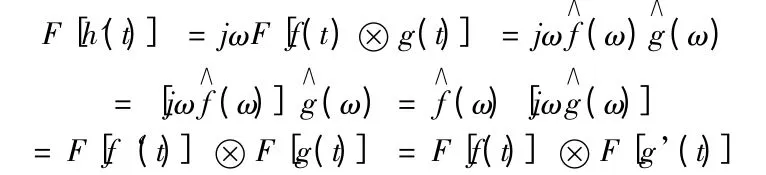
因此得到:h‘(t)=f’(t)⊗g(t)=f(t)⊗g'(t)

假如将函数f(t)看作是一个信号，g(t)看作是一个滤波器，那么滤波器与信号的导数的卷积就可以看作是信号与滤波器的导数的卷积。我们选g(t)为高斯函数，应用它的导数就能构造Morlet 小波和Maar 小波，所以，小波变换的突变点和极值点与信号f(t)的突变点和极值点具有相对应的关系，应用小波就可以检测到突变信号。具体的过程如下:

设θ(t)是一个起平滑作用的低通平稳函数，并且满足条件

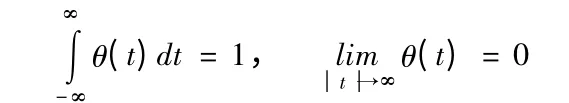
我们取θ(t)为高斯函数，即

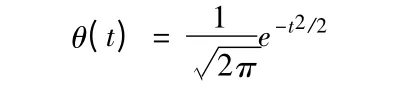
假设θ(t)是二次可导的，并且定义

则函数ψ(1)(t)、ψ(2)(t)满足小波的容许条件:

所以可以用做小波基函数。

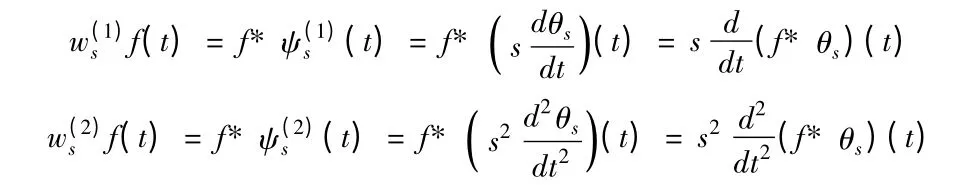
如上所述，小波变化w(1)sf(t)，w(2)sf(t)分别是函数f(t)在尺度s下由θ(t)平滑后再取一阶、二阶导数。当s 比较小的时候，用θs(t)对f(t)平滑的效果对f(t)的突变点位影响还不算大;当s 比较大的时候，此平滑过程能将f(t)的某些细小的突变点消弱，并且只剩下较大尺寸的突变。所以，当小波函数可以看作是某一平滑函数的一阶导数时，信号小波变换模的局部极值点对应信号的突变点(或边缘)。当小波函数可以看作是某一平滑函数的二阶导数时，信号小波变换模的过零点，也对应信号的突变点(或边缘)。这就是通过检测小波变换系数模的过零点和局部极值点可以检测信号突变点(或边缘)的基本原理。

2 数据突变点识别仿真模拟

数据信号的突变点在数学上我们把它分为两种:一是数据在某时刻，其值发生突然变化，使数据信号产生不连续性，这种突变点是第一类间断点;另一种是数据信号外观上看很平滑，其值看不出突然变化，但在数据信号的一阶微分上有突变发生，且一阶微分不连续，称此为第二类间断点。

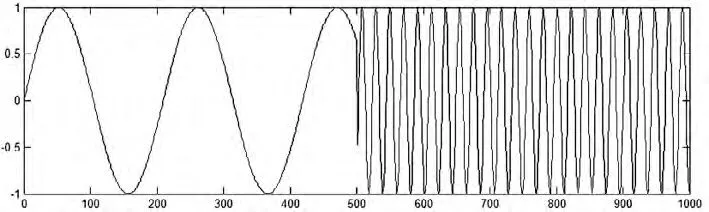
图1 第一类间断点信号波形

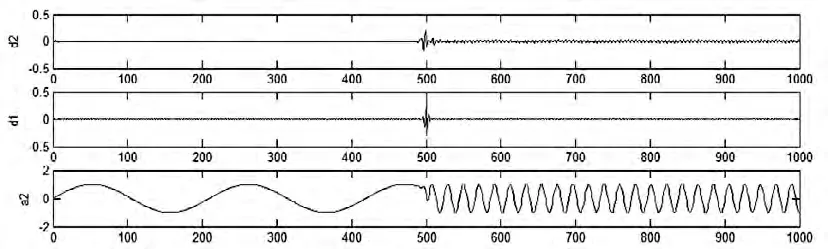
图2 两层db5 小波分解细节和逼近信号

2.1 模拟第一类间断点识别

第一类间断点突变信号如图1 所示，信号的间断是在低频正弦信号的后半部分加入了中高频正弦信号。应用db5 小波进行2 层分解来检测，得到的细节信号如图2 所示。从图中可以看出，细节信号能清楚显示间断点的位置。

图3 第二类间断点信号波形

图4 五层db2 小波分解细节和逼近信号

2.2 模拟第二类间断点识别

第二类间断点突变信号如图3 所示，它是一条光滑平缓的斜线，但一阶微分有突变点。用db2 小波对信号进行5 层分解，得到前两层的细节信号如图4 所示。可以看到，细节信号能清楚的将信号的第二类间断点显示出来了。

3 数据突变点识别实例应用

下面以某桥梁上安装的位移计数据为例，应用小波变换进行处理，观察处理结果与实际情况的对比。

图5 伸缩缝位移计数据

图5 是桥梁伸缩缝处安装的位移计数据，随温度的变化伸缩缝位移逐渐变小，在某处经过超重车辆时有明显位移变化，截取部分数据放大后，可以看到数据跳变。但在海量数据处理时并不容易发现，此时应用小波变换就就能很快的找到突变点的位置。

图6 六层db2 小波分解细节

图6 是6 层db2 小波分解细节，从图中可以看出，小波变换细节信号能清楚的将该数据的突变点识别出来，并且逼近信号a5 很好的表现了数据变化的整体趋势。

4 结论与建议

本文应用小波变换对自动化监测数据进行突变点识别，并应用db小波基做了仿真模拟实验。在此基础上，对桥梁伸缩缝安装的位移传感器数据进行小波变换，识别其突变点，取得了较好的效果。归纳起来有几下几点:(1)小波变换具有多尺度性质，仿真模拟与实际数据的处理都说明小波变换是数据突变点识别较好的方法，它比传统方法具有更多优越性。(2)小波母函数的对称性对于数据的重构和偏移有一定的影响，对称性不好，处理后得到的数据一般会有一定量的位置偏移。在实例分析中，也发现了位移计数据突变点的位置识别会有些许偏差。(3)应用小波变换处理数据时，数据边界会发生一些畸变。可应用零延拓、镜像延拓、余弦延拓等方法进行扩边处理。

小波变换在处理数据时具有极大的优势，在自动化监测数据处理中有着广阔的发展空间和应用价值。

［1］杨福生，小波变换的工程分析与应用，北京，科学出版社，1999(2).

［2］彭玉华，小波变换与工程应用，北京，科学出版社，1999(9).

［3］胡昌华，张军波，夏军，张伟，基于MATLAB 的系统分析与设计——小波分析，西安，西安电子科技大学出版社，1999.

［4］赵红怡，武梦龙，曹淑琴，小波分析在突变信号检测中的应用，北京，北方工业大学学报，20004(3).