一种改进的基于KNN颜色线性模型抠图算法

向娅玲，杨卫英，谢志峰

（上海大学 影视艺术技术学院，上海 200072）

自然图像抠取[1-2]是图像处理和影视后期制作的关键技术之一，它的目的是对图像未知像素的透明度进行抠取以实现前景的准确提取。为了得到良好的抠取效果，大多数现有的软抠取方法需要用户输入三分图或涂鸦作为额外标记。

现有的软抠取算法大致可以归类为基于采样和基于传播的方法。基于采样[3-5]是应用不同参数或非参数模型，从未知像素附近选取确定的前景、背景样本估计得出未知像素的值。当采样的样本包含真实前景背景像素时，这种方法才能得到好的抠取结果。基于传播[6-9]通常假设图像在特征空间是局部平滑的，将已知区域的约束标记传播到未知区域来求解透明度值。当这类方法包含平滑假设，才会得到较好的实验结果。

为了使软抠取算法对图像包含平滑区域或是孔洞、纹理区域都能有好的抠取效果，本文提出了一种改进的基于KNN颜色线性模型软抠取算法[10]。首先，在特征向量参数选取上增加了一个参数——焦点信息；然后使用基于KNN的颜色线性模型将非局部原理和平滑假设相结合，使本文改进算法适用上述场景。本文采用针对大型图的谱聚类算法，减少用户的标记输入。用户只需要在聚类后的结果中选择确定的前景、背景区域中的某一像素，就能生成三分图。同时也可将生成的三分图应用到本文的抠图算法或者文献[6-8]的算法中。

1 相关工作

图像I可表示为前景图像F和背景图像B的线性组合[11-12]

式中：i（x，y）代表图像像素i的坐标；αi代表像素i的透明度。图像抠取算法的关键是精确估计透明度α值。在现有的众多图像抠取算法中，主要介绍与本文密切相关的两个算法：闭形式软抠取和KNN软抠取。

1.1 闭形式软抠取

闭形式软抠取算法假设图像的前景背景颜色局部平滑并且满足颜色线性模型假设，即在一个很小的局部窗内透明度α值可由RGB空间内图像的3个颜色通道线性表示

式中：a=1/(F -B)，b=-B/(F -B )。这个模型使得每个像素被若干重叠的局部窗覆盖，从而用户的输入可以有效地进行传播。有了这一假设，就可以定义关于透明度α的代价函数，即

目标函数对于每个未知变量都是二次型的，消除ac和b，得到了只含有未知量为α的二次目标函数

式中：L是一个N×N的抠图拉普拉斯矩阵（N表示像素总和），可以通过闭形式对该函数求解。

1.2KNN软抠取

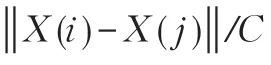
2 ESCG算法对图像进行谱聚类

目前绝大多数自然图像软抠取算法都是聚焦在如何得到更好的抠取结果，但求解图像α值是一个欠约束问题，需要额外的用户标记。这就引出一个问题：什么样的输入是好的用户输入，使得该算法能给出最精确的结果？

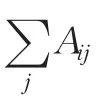
本 文 使 用 ESCG[13]（Efficient Spectral Clustering on Graphs）算法对图进行谱聚类，将源图像映射为图G，连接其中像素节点i，j的边的权重由核函数k（i，j）[1]给出

随机挑选G中的d个种子点作为超级节点，计算这些节点到G中剩余点的最短距离，在运用Dijkstra算法求解最短路径之前，首先对W矩阵中边的权重进行如下转化

根据最短路径将G中所有节点分成d个子集，这些子集与d个超级节点的关系便可建立二值矩阵R∈ ℜd×n，接着通过公式Wˆ=RW 将图像G对应的图转化为二分图。二分图对应的拉普拉斯矩阵为

将矩阵U每一行中的项看作k维空间的一个点后，可用k-means算法将所有节点划分为k个类。

实验通过本文算法与非局部软抠取中使用的谱聚类算法结果比较，发现聚类个数选择在12～15之间便能很好地将图像归类到前景/背景区域。对于比较简单的图像，聚类个数设置在8～10即可。而对于那些前景背景非常复杂的图像，k值往往需要选取较大，一般在30左右。谱聚类之后，只需用户选择确定的前景、背景区域中某一像素来进行手动标记，那些未被标记的视为未知区域。通过这一步骤生成的三分图以及将本文及非局部软抠取算法生成三分图分别作为KNN软抠取、非局部软抠取算法的输入得到的结果如图1所示。分别将本文和非局部软抠取中谱生成的三分图作为额外的输入，采用相同的抠取算法得到结果为图1d与图1e，可以看出图1d的抠取结果要优于图1e。

由上述实验结果可知，本文的谱聚类算法比Nonlocal谱聚类算法生成三分图的未知像素区域缩小，尤其对树叶等包含孔洞的图像未知区域的标注更精确，从而降低了后续估算α值的计算量。

图1 本文与非局部软抠取算法生成三分图及抠图结果比较

3 改进的基于KNN颜色线性模型抠图算法流程

本文假设改进算法在特征空间内符合颜色线性模型。下文中主要讨论特征向量的选取、使用基于KNN颜色线性模型[10]构造目标函数求解透明度α值。

3.1 特征选取

受文献[15]的启发，本文使用的特征矢量包括颜色、空间坐标以及焦点信息，对于一个给定的像素点i，它的特征矢量X（i）可以表示为

3.2 二次目标函数求解

闭形式软抠取算法采用的线性模型假设像素i的前景F和背景B在局部窗内位于RGB颜色空间某一直线上，满足这一假设的图像才能得到好的抠取效果。而KNN算法在抠取图像场景包括毛发等效果欠佳的原因也是因为没有局部平滑假设。为了改善抠取结果，本文使用文献[10]提出的基于KNN的线性颜色模型抠图算法来进行图像抠取。

式中：I是输入源图像；C是颜色通道。为了估算透明度α值，通过消除式（11）中的参数ac和b后目标函数可表示成如下闭形式函数

这是一个关于α的二次式，通过求解线性系统得到其值。其中，α 是一个 N×1的矩阵，L是N×N的矩阵，第（j，k）项[10]元素表示如下

式中：N是像素的数目；Σi是3×3的协方差矩阵；μi是一个3×1的矩阵，指像素i最邻近像素Ni的颜色平均值；ε为一个数值很小的系数，本文实验中设为10-7。当用户提供额外的标注信息，透明度α值求解通过最小化如下带约束的代价函数

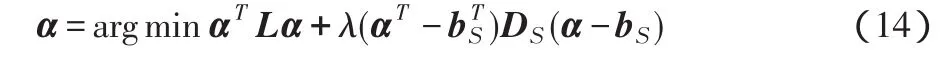
式中：λ为一常数，在本文中取值为100；Ds是一个对角矩阵，标记了的像素在Ds对角元素中的值为1，其他像素对应的值为0；bS是一个矢量，标记了的像素对应其α值，其他未知像素对应的值为0。式（14）是二次的，它的最小化通过求解一个稀疏线性方程来实现。为了减少求解稀疏方程的时间复杂度，本文使用共轭梯度法。α的最优解为

4 实验结果

为了评估本文所提算法的抠图性能，本文对闭形式软抠取、KNN软抠取以及本文改进算法的抠图准确度进行比较。所有用于实验的源图像、三分图、ground-truth等数据集都来自文献[17]提供的网站。

表1 3种抠图算法的性能比较

选择文献[18]中的4幅图像（见图2）进行实验，这些图像包含毛发、孔洞以及前背景颜色近似等场景。由表1可以看出，本文算法与其他实验算法相比在前述场景都能得到较小的误差值，而其他算法只能在各种适用的场景取得较好结果。

图2 4种抠图算法结果比较

图2列出图像的抠取结果，闭形式软抠取算法在对如GT09所示的绒毛物品，包含平滑过渡的区域抠取效果在输入的4幅图像中是最佳，因为这区域平滑假设是适用的。KNN软抠取算法在抠取包含孔洞的物体时性能优于其他算法，但在计算相邻像素的相似度时，使用数值很小的特征差值来衡量，这就导致绝大部分像素的α值趋近0或1，抠取得到的结果更接近硬分割。本文改进的算法在抠取毛发、孔洞区域的性能接近或优于闭形式、KNN软抠取算法，在前景、背景相似的区域抠取效果在这4种算法中是最佳的。图3为使用本文算法对GT16图像抠取结果的放大显示，它在这4种算法得到的结果是最佳的。

图3 本文算法更清晰实验结果

5 结论

本文在基于KNN颜色线性模型抠图算法的基础上提出了一种改进算法。该方法通过谱聚类生成三分图，减少用户输入；考虑了非局部原理，对孔洞、纹理区域能得到很好的抠取结果；在特征空间考虑平滑因素，对毛发区域也能取得平滑的效果。由于构造特征向量时添加了焦点特征，这在图像前景背景某些局域颜色信息近似时十分有效。上述实验表明所提算法能比本文实验的其他几种算法得到更好的结果。

[1] 于晏平.基于能量和取样的图像抠取算法研究[D].北京：北京交通大学，2012.

[2] 关宇东，韩媞.复杂背景下基于分割逼近法的抠像技术研究[J].电视技术，2007，31（7）：75-76.

[3] 吕巨建，战荫伟.一种改进的Bayes抠图算法[J].计算机工程，2010，36（3）：213-214.

[4]SHAHRIAN E，RAJAN D.Weighted color and texture sample se⁃lection for iamge matting[C]//Proc.2012 IEEE Conference on Computer Vision and Pattern Recognition.Washington，DC：IEEE Computer Society，2012：718-725.

[5] 黄睿，王翔.改进的自然图像鲁棒抠图算法[J].计算机工程与应用，2013，49（12）：136-139.

[6] LEE P，WU Y.Nonlocal matting[C]//Proc.2011 IEEE Conference on Computer Vision and Pattern Recognition.Washington，DC：IEEE Computer Society，2011：2193-2200.

[7]CHEN Q F，LI D，TANG C K.KNN matting[J].IEEE Trans.Pat⁃tern Analysis and Machine Intelligence，2013，35（9）：2175-2188.

[8] LEVIN A，LISCHINSKI D，WEISS Y.A closed form solution to natural image matting[J].IEEE Trans.Pattern Analysis and Ma⁃chine Intelligence，2008，30（2）：228-242.

[9] SUN J，JIA J，TANG C K.Poisson matting[J].ACM Trans.Graph⁃ics，2004，23（3）：315-321.

[10] JIN M，KIM B K，SONG W J.KNN-based color line model for image matting[C]//Proc.2013 IEEE International Conference on Image Processing.Melbourne：IEEE Press，2013：2480-2483.

[11] 高正伟.图像前景提取技术研究[D].杭州：浙江大学，2008.

[12] 彭宏京，陈松灿，张道强.一种基于局部学习的自然图像景物提取方法[J].软件学报，2009，20（4）：834-844.

[13] LIU J，WANG C，DANILEVSKY M，et al.Large-scale spectral clustering on graphs[C]//Proc.23rd International Joint Confer⁃ence on Artificial Intelligence.Barcelona：AAAI Press，2013：1486-1492.

[14]SUBBARAO M，CHOI T S，NIKZAD A.Focusing techniques[J].Optical Engineering，1993，32（11）：2824-2836.

[15] SHI Y，AU O C，PANG J，et al.Color clustering matting[C]//Proc.2013 IEEE International Conference on Mutimedia and Ex⁃po（ICME）.[S.l.]：IEEE Press，2013：1-6.

[16] MUJA M，LOWE D G.Fast approximate nearest neighbors with automatic algorithm configuration[C]//Proc.4th International Con⁃ference on Computer Vision Theory and Applications.[S.l]：IN⁃STICC Press，2009：331-340.

[17]RHEMANN C，ROTHER C，WANG J，et al.A perceptually moti⁃vated online benchmark for image matting[C]//Proc.2009 IEEE Conference on Computer Vision and Pattern Recognition.Wash⁃ington，DC：IEEE Computer Society，2009：1826-1833.