PANS方法在双圆柱绕流数值模拟中的性能分析

杜若凡，阎超，罗大海

(北京航空航天大学 航空科学与工程学院，北京100191)

湍流问题由于其自身的复杂特性，已经成为制约计算流体动力学(Computational Fluid Dynamics，CFD)精确计算的瓶颈问题，极大地影响着CFD 预测的精度［1］.在当前条件下，RANS/LES 混合方法由于其经济性与有效性，相较于其他方法有较为明显的优势.近年来，研究者们发展了种类繁多的混合方法，包括DES(Detached-Eddy Simulation)方法［2］、SAS(Scale Adaptive Simulation)方法［3］、PANS(Partially Averaged Navier-Stokes)方法［4］以及 LNS(Limited Numerical Scales)方法［5］等.其中，PANS方法基于RANS方程进行修改，相比RANS方法对分离流动的模拟更为有效，但求解的尺度又远少于 LES求解的尺度［6］，PANS方法在单圆柱绕流［7］和跨声速空腔流动［8］等数值模拟中均得到了成功应用.

相比于上面提到的单圆柱绕流和跨声速空腔流动，双圆柱绕流问题更为复杂，包含丰富的流动现象，如湍流边界层、流动分离、自由剪切层失稳、涡脱落以及涡与圆柱壁面相互作用等，是考察湍流模拟方法的优秀算例.在 AIAA BANC［9］(Benchmark problems for Airframe Noise Computations)会议及欧盟 ATAAC［10］(Advanced Turbulence simulation for Aerodynamic Application Challenges)项目中，双圆柱绕流均是标准算例之一.该问题可视作对飞机起落架外形的简化，而起落架是飞机起降过程中噪声的主要来源，故该流动问题的研究对认识起落架绕流流场和分析噪声产生机理具有重要意义.

美国Langley研究中心对双圆柱绕流进行了多次实验［11-13］，获取了丰富可靠的实验数据.文献［9，14］对参与第一届BANC研讨会的众多组织机构的结果进行了汇总分析，并与实验数据进行对比，总结了 DDES(Delayed Detached Eddy Simulation)、FSM(Flow Simulation Methodology)、LES(Large Eddy Simulation)等不同湍流模拟方法对双圆柱绕流的模拟能力，发现不同方法得到的结果差异明显.文献［15］采用多种RANS/LES混合方法对双圆柱绕流进行模拟，对不同方法进行对比分析.文献［16］采用 DES(Detached-Eddy Simulation)和IDDES(Improved Delayed Detached-Eddy Simulation)等方法借助双圆柱绕流探讨数值耗散对计算结果的影响，取得了一些有意义的成果.在此选取该流动问题作为研究对象，对本文的PANS方法进行考察与评估.

1 计算方法

PANS方法以RANS方程为模板，本文采用的PANS方法基于两方程SST(Shear Stress Transport)模式，原始 SST 模式方程［17］为

式中:fk为模化湍动能ku与总的湍动能k的比值;fω为模化比耗散率ωu与总的比耗散率ω的比值.假定fk和fω是不随时间和空间变化的常数，从而SST模式方程转化为

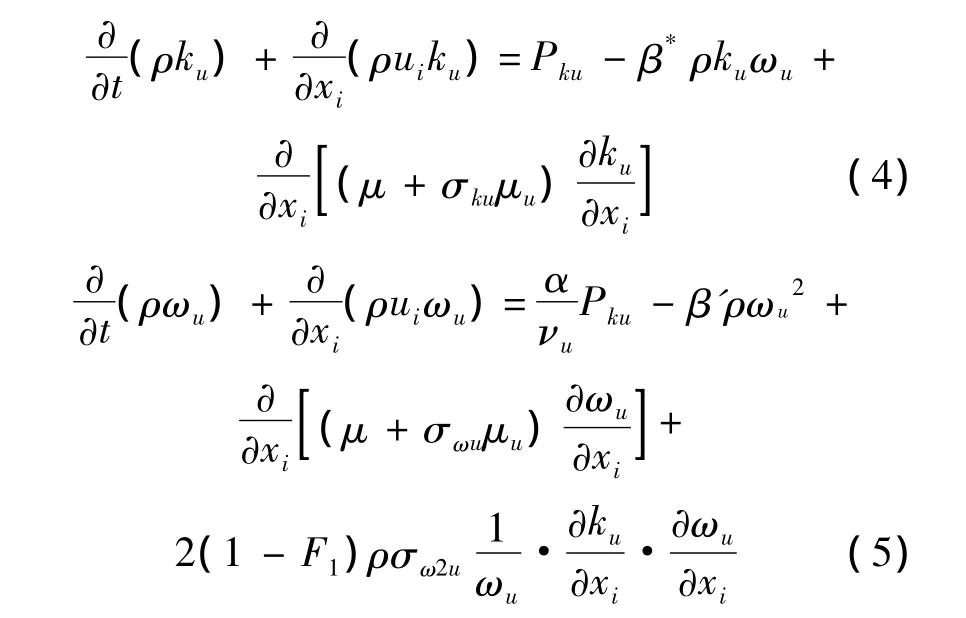
式中:修改后的模型常数分别为

模化的涡黏性系数μu和湍动能生成项Pku分别为

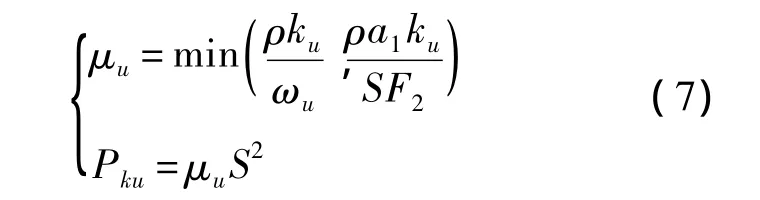
式中:ρ为密度;F2为混合函数;S为应变率;a1为常数;各参数详见文献［18］.

由此，通过将SST模式中的常数替换为与fk和fω有关的函数，较为便捷地得到了PANS方法模型方程.PANS方法中，通过调节fk和fω的值，决定模化的湍动能/耗散率的比例，进而确定求解的湍流尺度.对于高雷诺数流动，一般取 fω=1/fk，fk可选取不同的值［7］.然而对于复杂流动问题模拟，尤其是针对高雷诺数流动的近壁区，在计算网格密度达不到大涡模拟的要求时，采用RANS处理是更为合理的，此时fk在近壁区取值为1，PANS方法退化为RANS，而在其他流动区域(分离区或尾迹区)fk取值小于1，以求解部分的湍流尺度.因此，PANS方法中，fk可变的做法是更为合适的.但在方程(4)和方程(5)的求导过程中，可变fk的引入会增加额外的fk对于时间和空间的导数项(或称之为交换误差)，目前的PANS方法忽略了交换误差对计算结果的影响.

总之，对fk的取值方式可以分为两种，一种是让fk在整个计算域内取一个定值，本文中称为统一fk方法;另一种是让fk在不同区域取不同的值，本文称为可变fk方法，本文选取的具体fk分布函数［18］为

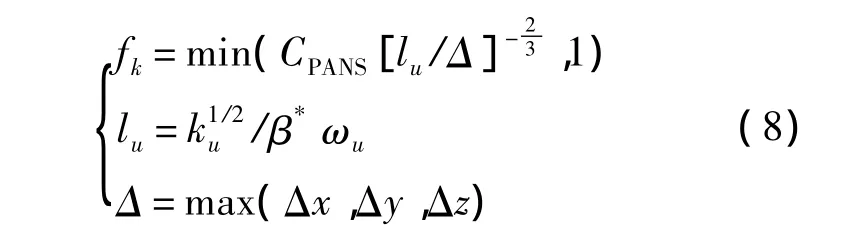
式中:lu为当地的湍流流动尺度;Δ为3个方向网格尺度Δx、Δy和Δz的最大值;CPANS为常数，此处取0.3.可以看出，可变fk方法中fk的取值取决于当地湍流尺度和网格尺度的比值，这一做法与SST DES模型中FDES函数的构造非常相似.近壁区和远场的湍流特征尺度很小，与网格尺度相比为小值，此时fk分布函数保证近壁区和远场处fk=1，PANS模型退化为RANS方程;在尾迹区，湍流特征尺度大于当地网格尺度，此时fk＜1，较小的fk使得PANS方法可以直接求解更多的湍流尺度，模型表现出更低的涡黏性，可以更为准确地捕捉尾迹区的流动结构.

2 计算结果与分析

双圆柱模型由两个直径相同的圆柱体沿来流方向排列而成，如图1所示，两圆柱体中心线之间的距离L=3.7D，D为圆柱直径，θ为圆柱方位角.坐标原点位于前圆柱圆心.自由来流马赫数Ma=0.1274，基于圆柱直径的雷诺数ReD=1.66×105.

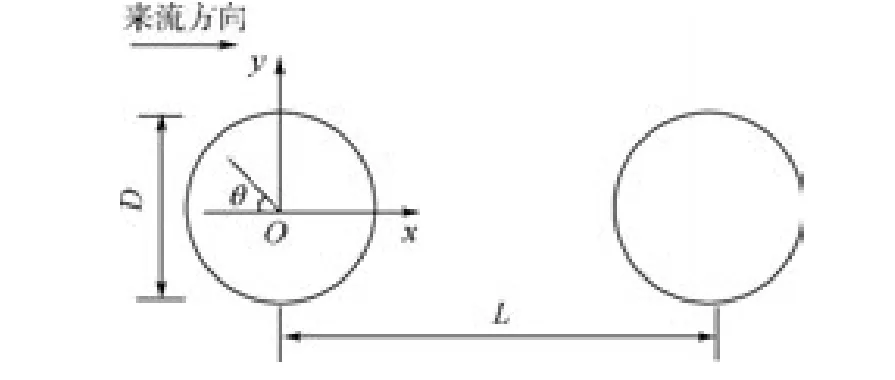
图1 双圆柱构型的xOy截面示意图Fig.1 Schematic diagram of xOy plane for tandem cylinders configuration

结合课题组以往计算经验［19-20］，进行网格生成与计算方法选择.计算网格如图2所示，在文献［10］提供的网格基础上进行修改得到，计算域流向×法向×展向为40D×20D×3D，网格总量约为625万，壁面第一层法向网格高度保证y+＜1，且在两圆柱中间区域以及后圆柱尾迹区域网格基本保持各向同性(即3个方向网格间距相同).对流项离散采用5阶WENO的Roe格式，黏性项采用4阶中心差分.壁面设置为无滑移绝热壁，展向边界设为周期性边界条件.时间步长取 Δt=5.9×10-5s，所得结果进行时间与展向平均.

图2 双圆柱构型计算网格示意图Fig.2 Schematic diagram of computational grid for tandem cylinders configuration

首先，结合瞬时流场，观察双圆柱绕流流动结构，分析各方法所得流场存在的差异，定性比较各方法的不同.

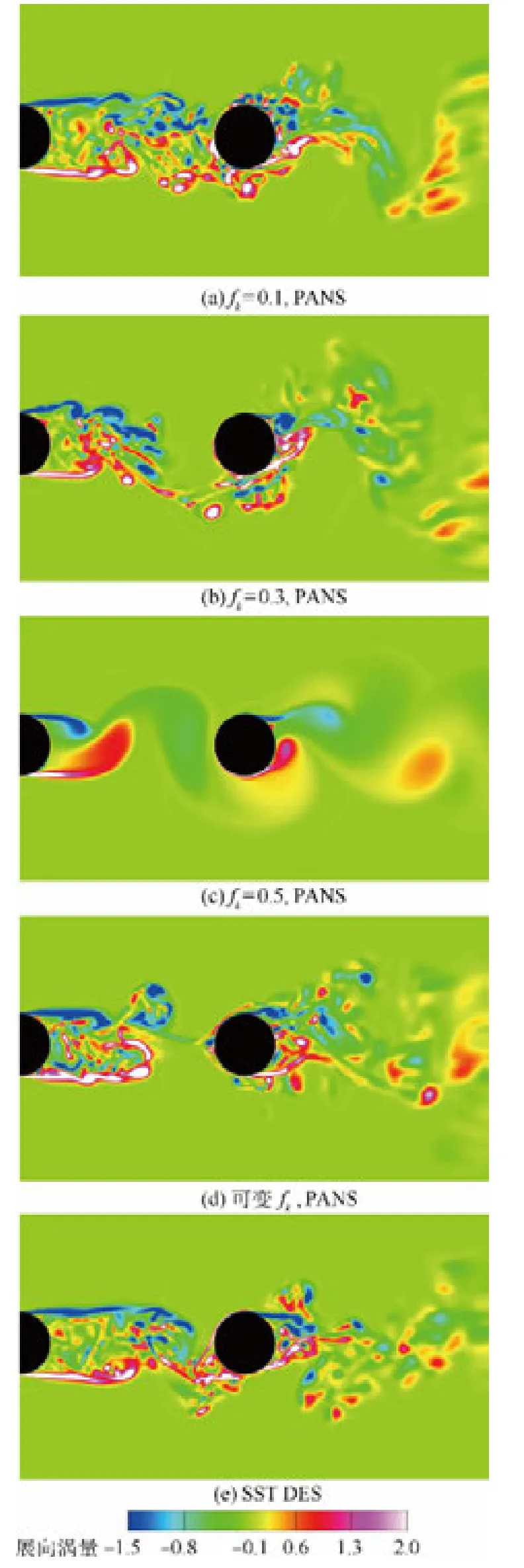
图3 不同方法瞬时展向涡量云图Fig.3 Contours of instantaneous spanwise vortices from different methods

图3为瞬时展向涡量云图，以图3(a)为例观察流动结构.来流经过前圆柱后拖出剪切层，剪切层逐渐发展，之后迅速失稳，二维涡结构逐渐发展为流向涡与展向涡相嵌套的三维涡结构，并出现复杂的周期性涡脱落.脱落的涡在两圆柱间相互作用，拉伸、变形、破碎，并进一步撞击到后圆柱壁面.涡撞击到后圆柱壁面后流动更加紊乱，与后圆柱剪切层相互作用，在尾迹区出现复杂的分离流动.对比图3中各结果，对于统一fk方法，随着fk取值增大，瞬时展向涡量云图中小尺度涡结构逐渐减少，且前圆柱剪切层长度存在差异:fk=0.1时，两圆柱间流动结构丰富、精细;fk=0.3时，剪切层长度明显减小，观察到的涡结构明显减少;fk=0.5时，所得结果与URANS结果类似，几乎看不到任何小尺度流动结构，完全不同于实验观测的结果.这是因为，在较大fk值下，过多的湍流脉动被模化，流场细节被严重抹平，与真实流动情况不符.对于可变fk方法，其求解湍流尺度的丰富程度介于fk=0.1与fk=0.3的统一方法之间.将本文PANS方法结果与SST DES 方 法 及 图 4［13］BART PIV(Particle Image Velocimetny)实验结果进行对比，除fk=0.5的统一方法外，各方法都可以表现出求解小尺度流动结构的能力.

图5为前、后圆柱壁面平均压力系数Cp分布，θ以上游驻点为0°，顺时针方向为正，如图1所示.前、后圆柱压力系数分布特点相似，均在90°位置出现压力峰值，圆柱背风面分离产生压力平台区，压力系数保持在-0.5左右.图5～图7中“EXP.1”来自文献［12］实验结果，“EXP.2”来自文献［13］实验结果.对前圆柱，fk=0.1的统一方法所模拟的压力峰值(绝对值)最小，分离提前;fk=0.3及fk=0.5时所得压力峰值高于实验值，分离推迟，分析认为这是由于其模拟的涡黏性偏高造成的.可变fk方法与实验结果及SST DES计算结果均吻合较好，差异不大.对后圆柱，不同方法所得结果的规律性与前圆柱一致，仍为可变fk方法和SST DES方法与实验结果最为接近.其中，可变 fk方法与“EXP.1”结果更为接近，SST DES方法更接近“EXP.2”的结果.

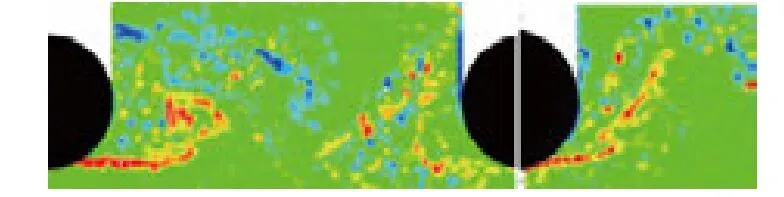
图4 BART PIV实验结果［13］Fig.4 Experimental results from BART PIV［13］

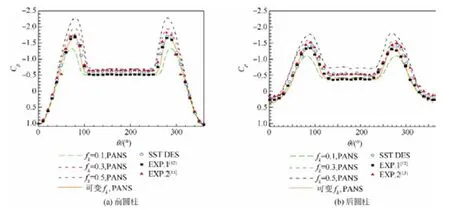
图5 双圆柱壁面平均压力系数分布Fig.5 Mean pressure coefficient distribution of surfaces of both cylinders

图6给出了不同方法流场中心线上平均流向速度分布的对比，横坐标为x坐标与D的比值，纵坐标为流向速度u与来流速度u∞的比值.流动经过前、后圆柱均出现分离区，对应平均流向速度小于0的区域.对比各方法，计算得到的分离区大小差异明显.对于统一fk方法，随着fk取值增大，所得分离区逐渐变小.可变fk方法与SST DES和实验结果均吻合较好，仅存在细微差异:在圆柱间区域，可变fk方法所得分离区略大于实验结果和SST DES结果;在后圆柱尾迹区，可变fk方法所得分离区稍小.需要注意的是，图6(b)中，“EXP.1”为后圆柱有转捩带装置的实验结果，可以看出转捩带对流向速度的实验结果有明显影响，可变fk方法和SST DES的计算结果与带有转捩带的实验结果更为吻合.

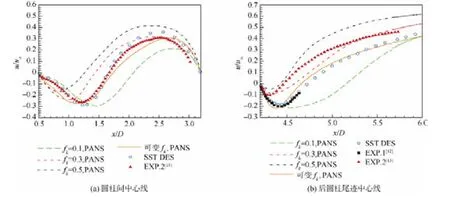
图6 中心线流向平均速度分布Fig.6 Mean streamwise velocity distribution at centerline

图7 中心线二维湍动能分布Fig.7 2D turbulence kinetic energy distribution at centerline

图8为可变方法计算的fk分布.在圆柱壁面附近的边界层区域及远场，fk被限制为1，保证该区域由RANS主导;在圆柱间及尾迹区等存在丰富涡结构的区域，fk取值大致在0.15～0.25.需要说明的是，fk在上游圆柱剪切层外由小值快速变化到1，该区域不由模型黏性主导，此处fk的快速变化对PANS模型黏性影响很小，从PANS模型计算结果与实验及DES结果的对比看来，fk快速变化导致的交换误差对PANS模型的正确求解影响不大.与统一fk方法相比，可变fk方法体现出较为明显的优势.分析认为，统一方法中fk难以取到最优值，尤其对于复杂流场，统一的fk取值难以满足不同区域的计算需要;可变fk方法考虑当地网格尺度与流动信息，兼顾不同区域的计算要求，对近壁区的流动合理地以RANS处理，同时通过调节fk的分布保证分离的剪切层和圆柱尾迹区更多的湍流尺度得以求解，适用于复杂流动模拟.

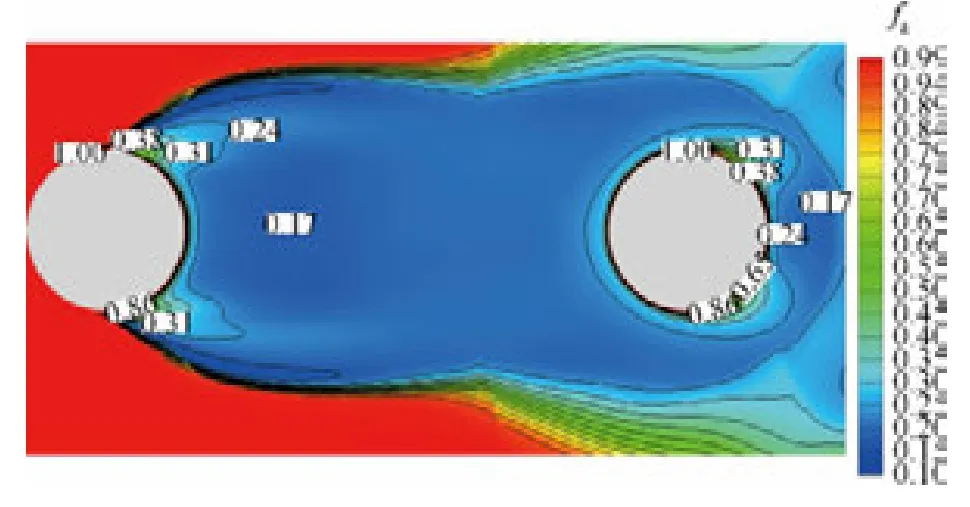
图8 可变fkPANS方法计算中fk的分布Fig.8 Distribution of fkfor variable fkPANS method

3 结论

1)对于统一fk方法，模型参数fk对计算结果有显著影响.随着fk取值增大，PANS方法模化更多的湍流尺度，展向流动受到抑制，小尺度涡减少，流动结构趋于粗糙，流动更多呈现出二维特征.与实验结果相比，fk=0.3、0.5所得结果流动分离推迟，分离区偏小，湍流脉动偏弱.而fk=0.1所得结果分离提前，分离区偏大，脉动过强，与实验同样存在明显差异.故对于双圆柱绕流，统一fk方法适应性不足，难以处理该复杂流动问题，无法给出令人满意的结果.

2)可变fk方法将模型参数fk与当地流动信息和网格尺度信息关联起来，构造fk在计算域内的分布函数，自动调节fk在不同流动区域的取值.计算结果表明，可变fk方法具有求解小尺度湍流结构的能力，所得涡结构丰富，流场正确合理.通过流场平均量及脉动量的对比分析，可变fk方法与SST DES计算结果及实验结果均吻合较好，相较于统一fk方法体现出了较为明显的优势，是一种具有工程应用前景的新型RANS/LES混合方法.

3)下一步研究工作中，考虑改进及构造新型的fk分布函数，以更为准确地模拟复杂湍流问题，并通过对方法更加深入地考察评估，将其进一步推向工程应用.

References)

［1］阎超，于剑，徐晶磊，等.CFD模拟方法的发展成就与展望［J］.力学进展，2011，41(5):562-589.Yan C，Yu J，Xu J L，et al.On the achievements and prospects for the methods of computational fluid dynamics［J］.Advances in Mechanics，2011，41(5):562-589(in Chinese).

［2］ Spalart P R，Jou W H，Strelets M，et al.Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach［C］∥Proceedings of 1st AFOSR International Conference on DNS/LES，Advances in DNS/LES.Columbus:Greyden Press，1997:137-147.

［3］ Menter F R，Kuntz M，Bender R.A scale-adaptive simulation model forturbulent flow predictions，AIAA-2003-0767［R］.Reston:AIAA，2003.

［4］ Girimaji S S，Srinivasan R，Jeong E.PANS turbulence model for seamless transition between RANS and LES:Fixed point analysis and preliminary results［C］∥Proceedings of ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference.New York:ASME，2003，2:1901-1909.

［5］ Batten P，Goldberg U，Chakravarthy S.Reconstructed sub-grid methods for acoustics predictions at all Reynolds numbers，AIAA-2002-2511［R］.Reston:AIAA，2002.

［6］ Frendi A，Tosh A，Girimaji S S.Flow past a backward-facing step:Comparison of PANS，DES and URANS results with experiments［J］.International Journal for Computational Methods in Engineeing Science and Mechanics，2007，8(1):23-38.

［7］ Lakshmipathy S，Reyes D A，Girimaji S S.Partially averaged Navier-Stokes method:Modeling and simulation of low Reynolds number effects in flow past a circular cylinder，AIAA-2011-3107［R］.Reston:AIAA，2011.

［8］ Basu D，Hamed A，Das K.Assessment of partially averaged Navier-Stokes(PANS)multiscale model in transonic turbulent separated flows［C］∥Proceedings of FEDSM，5th Joint ASME/JSME Fluids Engineering Conference.New York:ASME，2007，2:1451-1459.

［9］ Lockard D P.Summary of the tandem cylinder solutions from the benchmark problems for airframe noise computations-I workshop，AIAA-2011-0353［R］.Reston:AIAA，2011.

［10］ Schwamborn D.Results and lessons learned from the EU-project ATAAC［C］∥ERCOFTAC Symposium Unsteady Separation in Fluid-Structure Interaction.Mykonos，Greece:［s.n.］2013，6:17-21.

［11］ Jenkins L N，Khorrami M R，Choudhari M M，et al.Characterization of unsteady flow structures around tandem cylinders for component interaction studies in airframe noise，AIAA-2005-2812［R］.Reston:AIAA，2005.

［12］ Hutcheson F V，Brooks T F.Noise radiation from single and multiple rod configurations，AIAA-2006-2629［R］.Reston:AIAA，2006.

［13］ Jenkins L N，Neuhart D H，Mcginley C B，et al.Measurements of unsteady wake interference between tandem cylinders，AIAA-2006-3202［R］.Reston:AIAA，2006.

［14］ Lockard D P，Khorrami M R，Choudhari M M，et al.Tandem cylinder noise predictions，AIAA-2007-3450［R］.Reston:AIAA，2007.

［15］ Weinmann M，Sandberg R D，Doolan C.Flow and noise prediction for a tandem cylinder configuration using novel hybrid RANS/LES approaches，AIAA-2010-3787［R］.Reston:AIAA，2010.

［16］ Xiao Z X，Liu J，Huang J B，et al.Numerical dissipation effects on massive separation around tandem cylinders［J］.AIAA Journal，2012，50(5):1119-1136.

［17］ Menter F R.Two equation eddy-viscosity turbulence models for engineering applications［J］.AIAA Journal，1994，32(8):1598-1605.

［18］ Luo D H，Yan C，Liu H K，et al.Comparative assessment of PANS and DES for simulation of flow past a circular cylinder［J］.Journal of Wind Engineering ＆ Industrial Aerodynamics，2014，134:65-77.

［19］刘佳，阎超，赵瑞，等.DES方法对返回舱气动热环境数值模拟［J］.北京航空航天大学学报，2013，39(5):590-594.Liu J，Yan C，Zhao R，et al.Simulation of re-entry capsule thermodynamics environment by DES method［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(5):590-594(in Chinese).

［20］李君哲，阎超，柯伦，等.气动热CFD计算的格式效应研究［J］.北京航空航天大学学报，2003，29(11):1022-1025.Li J Z，Yan C，Ke L，et al.Research on scheme effect of computational fluid dynamics in aerothermal［J］.Journal of Beijing University of Aeronautics and Astronautics，2003，29(11):1022-1025(in Chinese).